利用 COMSOL Multiphysics 拟合实验数据曲线

在 COMSOL Multiphysics 中，我们通常需要使用实验数据来表示材料属性或模型的其他输入项。但是，实验数据通常有许多噪点，并会包含我们不希望引入仿真中的实验错误。在这篇博客中，我们将研究如何借助 COMSOL Multiphysics 的核心功能来为实验数据拟合平滑的曲线与表面。

作为最小化问题的曲线拟合

我们先看下图所示的部分实验数据样本，可以观察到数据包含噪点，而且取样在 x 轴上不均匀。这一实验数据可能代表了一种材料属性，如果这一属性依赖于解变量，例如依赖于温度的导热系数，我们通常就不希望直接在分析中使用这一数据。
这类含噪点的输入数据通常会增加求解器的收敛难度，具体原因请阅读博客“求解非线性静态有限元问题”。相反，如果我们能用一条平滑曲线对数据进行近似，通常就可以改进模型的收敛，还能得到一个简单的函数来表示材料属性。

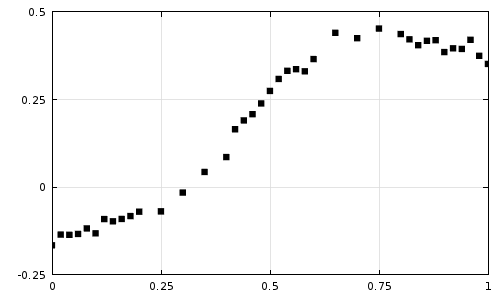
希望用更简单的函数来近似实验数据。

我们希望找到一个函数 F(x) 来尽可能接近地拟合实验数据 D(x)。我们将定义一个“最拟合”函数来最小化实验数据与拟合函数之差的平方，然后在整个数据范围进行积分。也就是说，我们的目标是最小化：

因此，我们首先需要决定希望拟合哪类函数。我们可以灵活选择所用的函数类型，但应选择一个可得到数值良态问题的拟合函数。我们依据最高鲁棒性的原则选择了这一拟合函数，不过这里将不会对选择原因展开介绍：

此时，a=0, b=1 可以简化为：

现在，我们需要找到 4 个系数来最小化：

虽然这可能听起来像一个优化问题，但我们的系数并没有任何约束，且假定上述函数有单一最小值。该最小值对应于导数为零时的相对系数。也就是说，要找出最拟合函数，我们必须找到以下条件下的系数值：

事实证明，我们能够利用 COMSOL Multiphysics 的核心功能求解该问题。我们再来看一下如何实现。

在 COMSOL 中执行

我们先创建一个包含一维分量的新文件。我们将使用‘全局常微分和微分代数方程’物理场接口来求解系数，并使用稳态求解器。简单起见，我们将使用无量纲长度单位，如下方截屏所示。

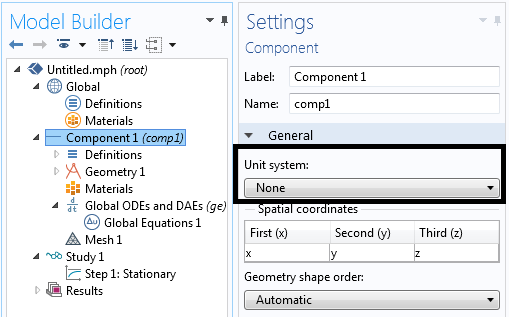
从一维分量开始，并将‘单位系统’设为‘None’。

接下来，创建几何。我们的几何应包括‘间隔’，本例中采样点的范围是从 0 到 1），以及每个采样点沿 x 方向的一组点。您可以简单地从电子表单中复制这些点的范围，然后粘贴到‘点’特征下，如下图所示。

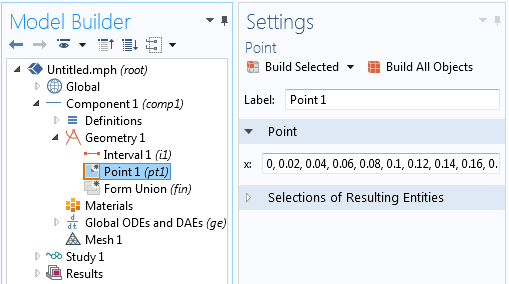
在间隔内为每个数据采样点增加点。

使用内插函数读取实验数据。为函数输入一个合适的名称，我们在下方截图中将其简单命名为 D，选择“使用空间坐标作为自变量”，并确保在数据点间使用缺省的‘线性’内插。

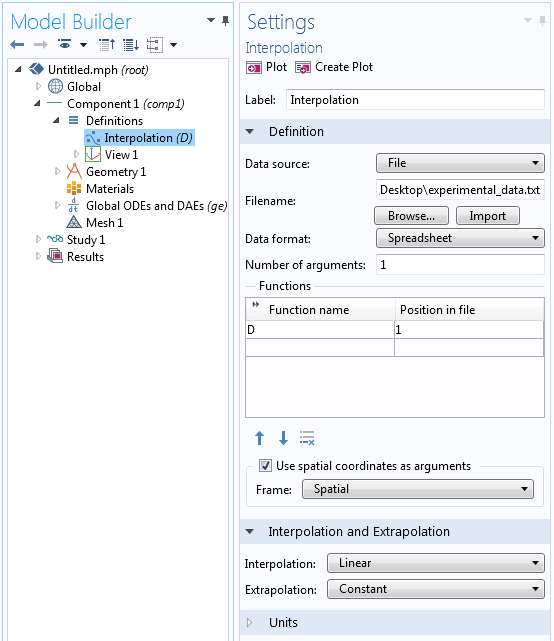
导入实验数据的设定。

针对所有域定义一个‘积分算子’。您可以使用缺省名称：intop1。本特征可以用于执行上述积分操作。

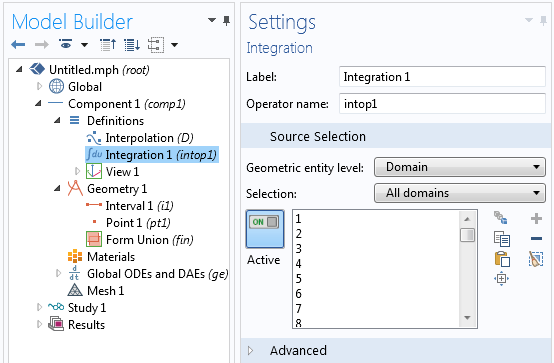
针对所有域定义积分算子。

现在定义两个变量。一个是您的函数 F，另一个是我们希望最小化的函数 R。由于‘几何实体层次’设为‘整个模型’，将在模型所有域定义 F，并将随函数 x 在空间变化。另一方面，R 在各处均为标量值，而且也在整个模型可用。如下方截图所示，我们可以输入 F 作为 c_0,c_1,c_2,c_3 的函数，并在之后定义这些系数。

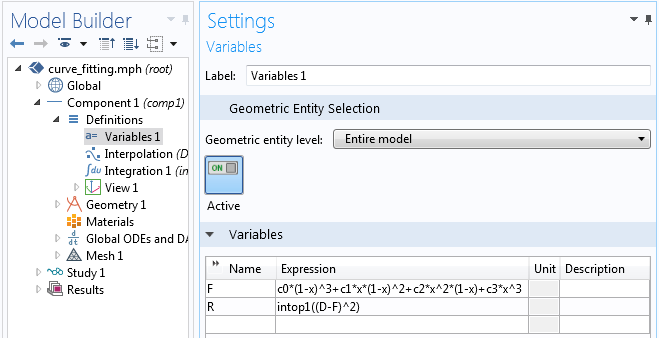
拟合函数的定义，以及希望最小化的量。

接下来，我们将使用‘全局方程’ 接口来为这四个系数定义四个方程。还记得我们之前希望 R 的导数能相对于每个系数为零吗？使用差分算子 d(f(x),x)，我们可以按照下图所示输入：

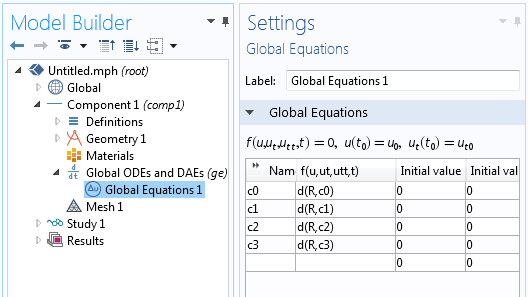
‘全局方程’用于求解拟合函数的系数。

我们最终需要一个适合一维域的网格。还记得之前我们在每个数据采样点安置了一个几何点吗？使用‘边网格’特征中的‘分布’子特征，可以保证每个数据点之间都存在一个单元。除此之外，我们无须更多单元，因为我们假定在数据点之间为线性内插，但我们也不接受更少的单元，因为这将会造成一些实验数据点的丢失。

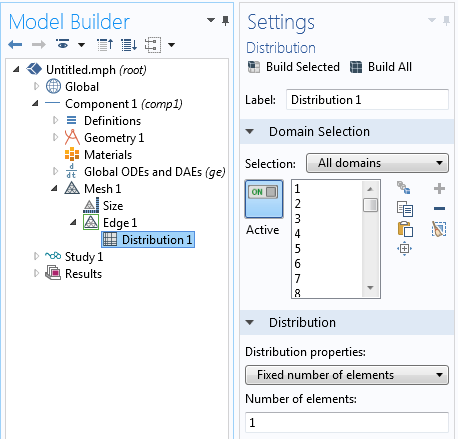
每个数据间隔都应存在一个单元。

我们现在可以求解该稳态问题来获取系数的值，并绘制结果。从下方的绘图中，我们可以看到数据点和它们之间的线性内插，以及计算得到的拟合函数。我们对这两条曲线之差的平方在整个间隔内进行了积分，并最小化了该值，现在有了一个非常近似我们数据的平滑简单函数。

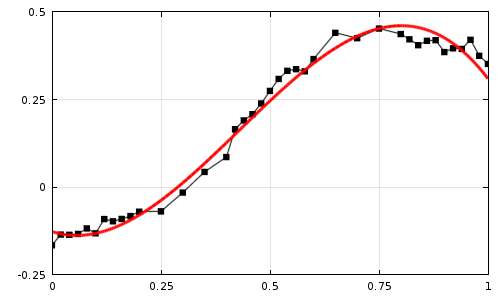
实验数据（黑色，含线性内插）以及拟合函数（红色）。

进一步拓展

到目前为止，我们的操作其实很简单，您可以在电子表格程序或其他任意数值软件工具中进行类似的曲线拟合计算。但这一方法的应用不止于此，我们也并非必须要使用该拟合函数。您可以自由任意函数，但最好是作为一组正交函数之和的函数。例如，试一下：

不过，请注意您只希望求解拟合函数内不同项下的线性系数。您不会希望使用类似 F(x) = c_0 + c_1sin ( \pi x /c_3 ) + c_2cos ( \pi x /c_4 ) 的非线性拟合系数，因为这类问题可能会因高度非线性而很难收敛。

如果您有一个二维或三维的数据集呢？您其实还可以继续使用我们这里所介绍的方法。唯一的区别是您将需要建立二维或三维域。您甚至可以将该域切换至一个不同的坐标系，而非必须使用笛卡尔坐标。

让我们快速查看下方所示区域内测量的一些数据采样点：

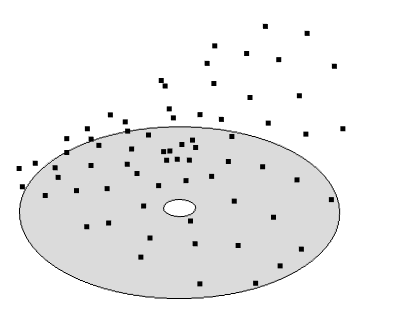
二维区域的采样数据。我们希望能有关于这些点高度的最佳拟合表面。

由于数据是在一个环状区域取样，似乎相对轴向和轴向 (r,\theta) 而非笛卡尔坐标方向有差异，我们可以尝试拟合该函数：

我们可以采用和之前相同的步骤。唯一的区别是我们需要在一个二维域而非一条线上进行积分，并使用柱坐标系书写表达式。

上述数据计算得到的最佳拟合表面。

结束语

您可以看到，COMSOL Multiphysics 软件提供了非常灵活的功能，您可以使用这里提到的方法找出一维、二维或三维数据的最佳拟合曲线。

有时候，您可能希望不只是一个简单的曲线拟合，希望考虑一些附加约束。这时，您可以使用优化模块，它不仅支持这类曲线拟合，还提供了更多的功能。有关使用优化模块进行曲线拟合和参数估计相关主题的简要介绍，您可以参考：

• 将材料模型数据曲线拟合至实验数据