
在之前的博客中,我们讨论了为了将材料参数拟合到材料模型中,我们需要正确的测量数据。我们还分析了一些典型的实验测试、材料模型选择对工作条件的考量,并通过示例演示了如何在非线性弹性模型中直接使用测量数据。我们今天将重点介绍如何将您的实验数据拟合到不同的超弹性材料模型中。
COMSOL Multiphysics 中的曲线拟合
获得测量数据后,问题随即变为:如何基于测量数据评估将用于定义超弹性材料模型的材料参数?实现方法之一是利用 COMSOL Multiphysics 的优化模块将参数化解析函数拟合到测量数据中。
在以下章节,我们将定义两类常见测试的应力-应变关系解析表达式,即单轴测试和双轴测试。这些解析表达式随后可以拟合到测量数据中,以获取材料参数。
各向同性、近似不可压缩超弹性
通过表征超弹性材料的体变形来评估材料参数,这可能会非常复杂。通常,我们会在评估参数时假定材料完全不可压缩。也就是说,通过曲线拟合评估材料参数后,由于不会再计算体积模量,所以必须为近似不可压缩超弹性材料使用一个较合理的体积模量值。
这里,我们会把测量数据拟合到几个完全不可压缩超弹性材料模型中。我们首先将介绍近似不可压缩公式中的一些基本概念,然后表征完全不可压缩下的应力测量。
对于近似不可压缩超弹性,总的应变能密度表示为:
其中,W_{iso} 是等体应变能量密度,W_{vol} 是体积应变能量密度,第二 Piola-Kirchhoff 应力为
其中 p_{p} 是体积应力、J 是体积比,C 是右 Cauchy-Green 张量。
您可以展开上述方程的第二项,这样,第二 Piola-Kirchhoff 应力张量可以同样表示为:
其中 \bar{I}_{1} 和 \bar{I}_{2} 是等体右 Cauchy-Green 张量 \bar{C} = J^{-2/3}C 的不变量。
第一 Piola-Kirchhoff 应力张量 P 和 Cauchy 应力张量 \sigma 可以表示为第二 Piola-Kirchhoff 应力张量的函数:
\sigma& = J^{-1}FSF^{T}
\end{align}
其中,F 是变形梯度。
注意:您可以在我们之前的博客 “为什么需要所有这些应力和应变?” 中读到有关各类应力测量的详细介绍。
应变能密度和应力通常以拉伸比 \lambda 的形式表示,拉伸比测量了变形的大小。在单轴拉伸实验中,拉伸比定义为 \lambda = L/L_0,其中 L 是样本的变形长度,L_0 是原始长度。在多轴应力状态下,您可以计算主参考方向 \hat{\mathbf{N}_a} 下的主伸缩 \lambda_a\;(a = 1,2,3),即主应力的方向。应力张量分量可以通过谱形式重写为
\sum S_{a} \hat{\mathbf{N}_{a}} \otimes \hat{\mathbf{N}_{a}}
其中 S_{a} 表示第二 Piola-Kirchhoff 应力张量的主值,\hat{\mathbf{N}_{a}} 表示主参考方向。您可以通过谱形式将右 Cauchy-Green 张量表示为
\sum\lambda_a^2 \hat{\mathbf{N}_a}\otimes\hat{\mathbf{N}_a}
其中 \lambda_a 表示主伸缩的值。这使您能通过主伸缩的函数来表示第二 Piola-Kirchhoff 应力张量的主值
现在,我们将考察首篇结构材料系列博客中介绍的单轴和双轴拉伸测试。我们可以推导出这两个测试中应力与应变间的一般关系。
假设不可压缩 (J=1),各向同性超弹性材料中单轴变形的主伸缩为
变形梯度为
在单轴拉伸 S_2 = S_3 = 0 中,体积应力 p_{p} 可通过以下公式估算
等体不变量 \bar{I}_{1_{uni}} 和 \bar{I}_{2_{uni}} 可以通过主拉伸 \lambda 表示为
\bar{I}_{1_{uni}} = \left(\lambda^2+\frac{2}{\lambda}\right) \\
\bar{I}_{2_{uni}} = \left(2\lambda + \frac{1}{\lambda^2}\right)
\end{align*}
假设不可压缩,各向同性超弹性材料中双轴变形的主伸缩为
在双轴拉伸 S_3 = 0 中,消去体积应力 p_{p} ,得到
不变量 \bar{I}_{1_{bi}} 和 \bar{I}_{2_{bi}} 随即为
\bar{I}_{1_{bi}} = \left( 2\lambda^2 + \frac{1}{\lambda^4}\right) \\
\bar{I}_{2_{bi}} = \left(\lambda^4 + \frac{2}{\lambda^2}\right)
\end{align*}
不可压缩超弹性材料模型中的应力与主拉伸
我们现在将分析几个最常见超弹性材料模型中应力与拉伸的关系。我们将出于曲线拟合的目的考察第一 Piola-Kirchhoff 应力。
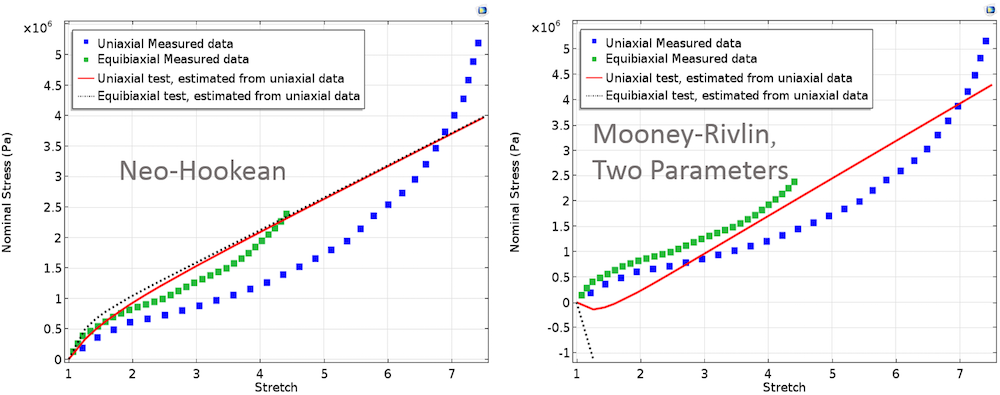
Neo-Hookean
Neo-Hookean 材料模型的总应变能密度为
其中 J_{el} 是弹性体积比率,\mu 是我们需要通过曲线拟合计算的材料参数。假设完全不可压缩,并使用方程 (1) 和 (2),单轴和双轴变形的第一 Piola-Kirchhoff 应力表达式将为
P_{1_{uniaxial}} &= \mu\left(\lambda-\lambda^{-2}\right)\\
P_{1_{biaxial}} &= \mu\left(\lambda-\lambda^{-5}\right)
\end{align*}
下方列出了其他一些超弹性材料模型中的应力与拉伸关系。这些关系式可以轻松使用方程 (1) 和 (2) 推导,它们将应力与应变能密度关联在了一起。
Mooney-Rivlin,两个参数
P_{1_{uniaxial}} &= 2\left(1-\lambda^{-3}\right)\left(\lambda C_{10}+C_{01}\right)\\
P_{1_{biaxial}} &= 2\left(\lambda-\lambda^{-5}\right)\left(C_{10}+\lambda^2 C_{01}\right)
\end{align*}
其中,C_{10} 和 C_{01} 是 Mooney-Rivlin 材料参数。
Mooney-Rivlin,五个参数
P_{1_{uniaxial}}& = 2\left(1-\lambda^{-3}\right)\left(\lambda C_{10} + 2C_{20}\lambda\left(I_{1_{uni}}-3\right)+C_{11}\lambda\left(I_{2_{uni}}-3\right)\\
& \quad +C_{01}+2C_{02}\left(I_{2_{uni}}-3\right)+C_{11}\left(I_{1_{uni}}-3\right))\right)\\
P_{1_{biaxial}}& = 2\left(\lambda-\lambda^{-5}\right)\left(C_{10}+2C_{20}\left(I_{1_{bi}}-3\right)+C_{11}\left(I_{2_{bi}}-3\right)\\
& \quad +\lambda^2C_{01}+2\lambda^2C_{02}\left(I_{2_{bi}}-3\right)+\lambda^2 C_{11}\left(I_{1_{bi}}-3\right))\right)
\end{split}
\end{align}
其中,C_{10}、C_{01}、C_{20}、C_{02} 和 C_{11} 是 Mooney-Rivlin 材料参数。
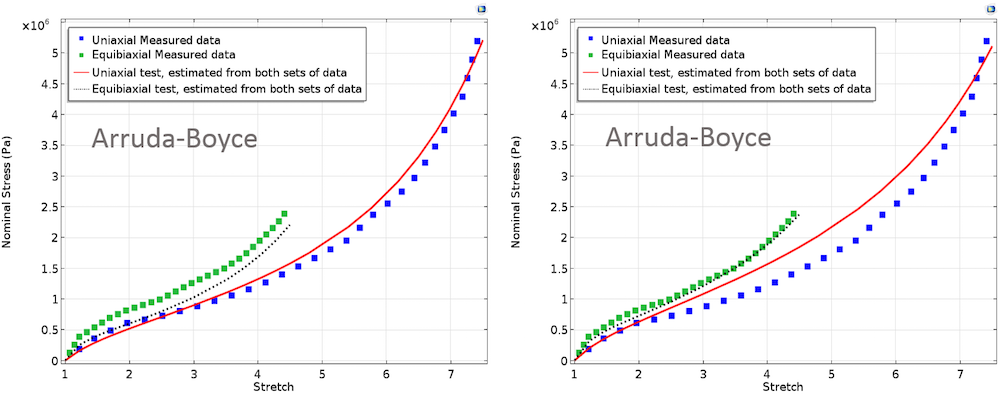
Arruda-Boyce
P_{1_{uniaxial}} &= 2\left(\lambda-\lambda^{-2}\right)\mu_0\sum_{p=1}^{5}\frac{p c_p}{N^{p-1}}I_{1_{uni}}^{p-1}\\
P_{1_{biaxial}} &= 2\left(\lambda-\lambda^{-5}\right)\mu_0\sum_{p=1}^{5}\frac{p c_p}{N^{p-1}}I_{1_{bi}}^{p-1}
\end{align}
其中,\mu_0 和 N 是 Arruda-Boyce 材料参数,c_p 是朗格文反函数中 Taylor 膨胀的前五项。
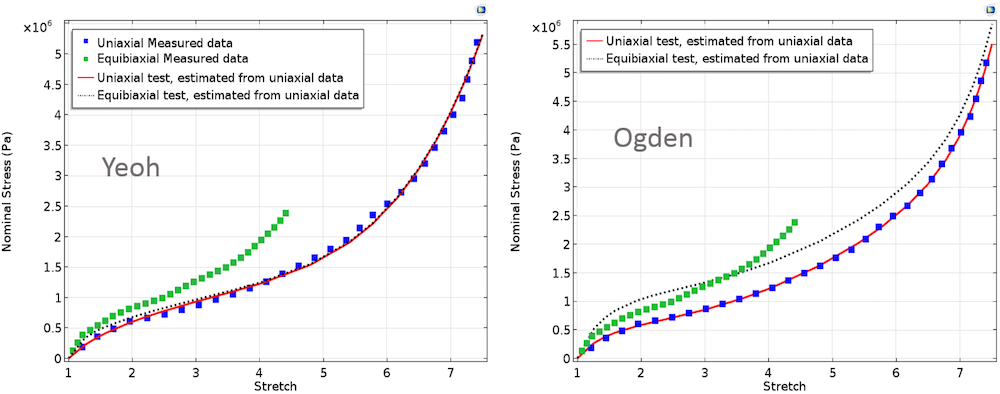
Yeoh
P_{1_{uniaxial}} &= 2\left(\lambda-\lambda^{-2}\right)\sum_{p=1}^{3}p c_p \left(I_{1_{uni}}-3\right)^{p-1}\\
P_{1_{biaxial}} &= 2\left(\lambda-\lambda^{-5}\right)\sum_{p=1}^{3}p c_p \left(I_{1_{bi}}-3\right)^{p-1}
\end{align}
其中,c_p 的值是 Yeoh 材料参数。
Ogden
P_{1_{uniaxial}} &= \sum_{p=1}^{N}\mu_p \left(\lambda^{\alpha_p-1} -\lambda^{-\frac{\alpha_p}{2}-1}\right)\\
P_{1_{biaxial}} &= \sum_{p=1}^{N}\mu_p \left(\lambda^{\alpha_p-1} -\lambda^{-2\alpha_p-1}\right)
\end{align}
其中,\mu_p 和 \alpha_p 是 Ogden 材料参数。
借助 COMSOL Multiphysics 的优化接口执行曲线拟合
我们将使用 COMSOL Multiphysics 的优化接口在上述解析表达式中拟合应力与拉伸的测量数据。注意:这里使用的材料数据是法向应力,可以定义为当前配置下作用在原始区域的力。针对适合的应力测量拟合测量数据非常重要。因此,我们需要针对第一 Piola-Kirchhoff 应力表达式的解析表达式拟合测量数据。下图显示了在硫化橡胶的单轴和双轴测试中测量得到的法向应力(原始数据)。
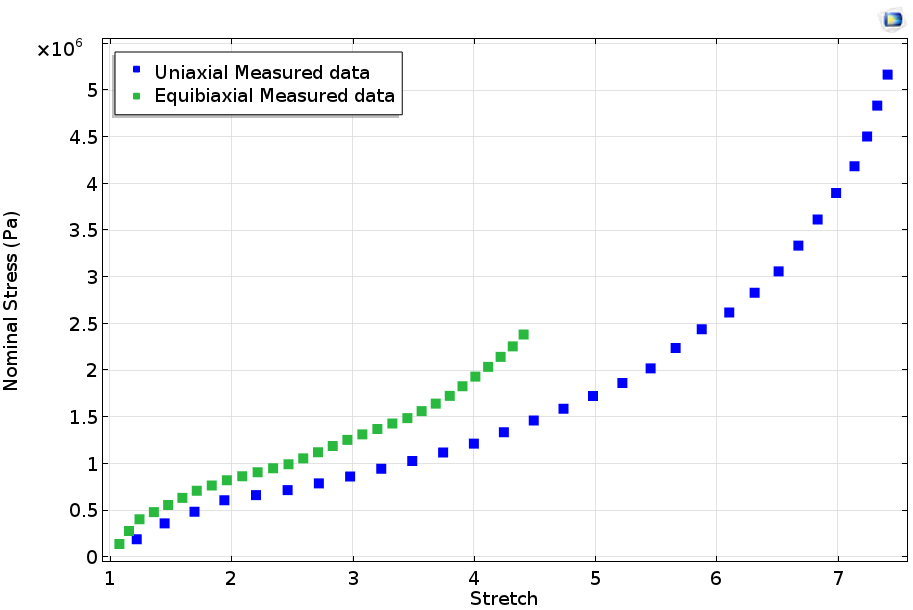
通过 Treloar 测量得到的应力-应变曲线。
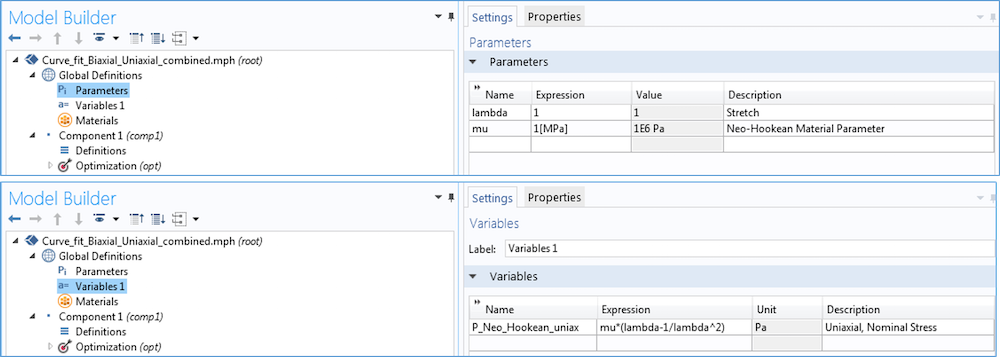
我们先从设定用于拟合单轴 Neo-Hookean 应力和单轴测量数据的模型开始。第一步是在零维模型中增加优化接口。零维表示我们的分析并不限定于特定几何。
接下来,我们将定义需计算的材料参数以及解析应力与拉伸关系的变量。下图为单轴 Neo-Hookean 材料模型中定义的参数和变量。
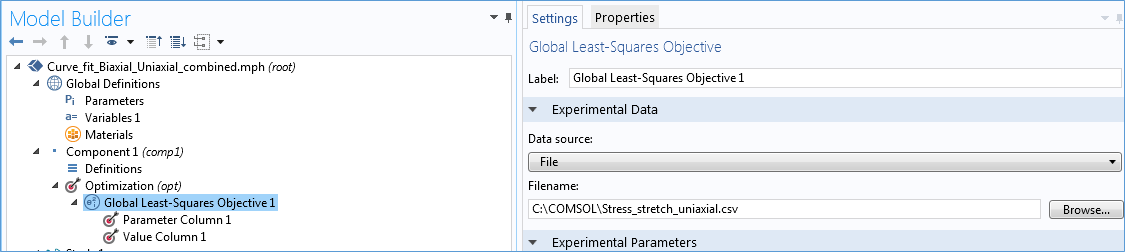
在优化接口增加全局最小二乘目标特征,通过输入文件指定单轴应力与拉伸的测量数据。接下来,增加参数列和值列。这里,我们将定义 lambda (拉伸)为测量参数,并将指定单轴解析应力表达式来拟合测量数据。我们还可以在表达式权重中指定一个权重因子。有关全局最小二乘目标特征设定的详细信息,您可以阅读我们 App 库中的 Mooney-Rivlin 曲线拟合教程。
我们现在可以开始求解以上问题,并能通过拟合单轴拉伸测试数据域单轴 Neo-Hookean 材料模型来评估材料参数。但这其实并不是一个好方法。如该系列的首篇博客所述,这一看似简单的测试其实有很多问题。在本篇博客的后半部分,我们将探讨仅基于一个数据集对材料执行校准的结果。
根据具体工作条件,您可以通过结合测量得到的单轴拉伸、压缩、双轴拉伸、扭曲和体积测试数据来更好地估算材料参数。这些编译的数据随后可以针对每个应用案例的解析应力表达式进行拟合。
这里,我们将同时使用双轴拉伸测试数据和单轴拉伸测试数据。既然我们已经针对单轴测试建立了优化模型,接下来将为双轴测试再定义一个全局最小二乘目标并将增加相应的参数和值列。在第二个全局最小二乘目标中,我们通过输入文件指定测量得到的双轴应力与拉伸数据文件。在值列,我们将指定双轴解析应力表达式来拟合双轴测试数据。
下图显示了优化研究步骤的设定。我们重命名了模型树分支以便反映所用的材料模型(Neo-Hookean)和这两个测试(单轴和双轴)。优化算法设为适用于求解最小二乘法类问题的 Levenberg-Marquardt 求解器。模型设定完毕,现在可以优化两个全局最小二乘目标的和,即单轴和双轴测试情况。
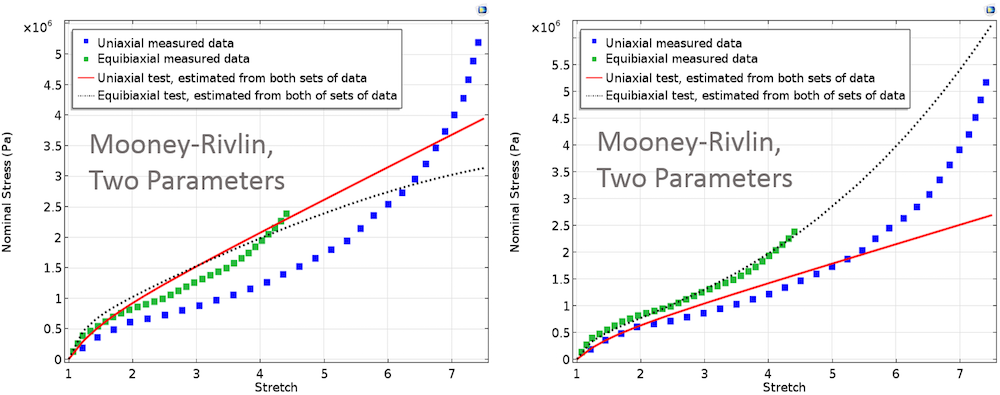
下图针对测量数据绘制了拟合数据。为单轴和双轴最小二乘拟合指定了同等权重。显然,只包含一个参数的 Neo-Hookean 材料模型的拟合不好,因为测试数据为非线性而且包括一个拐点。
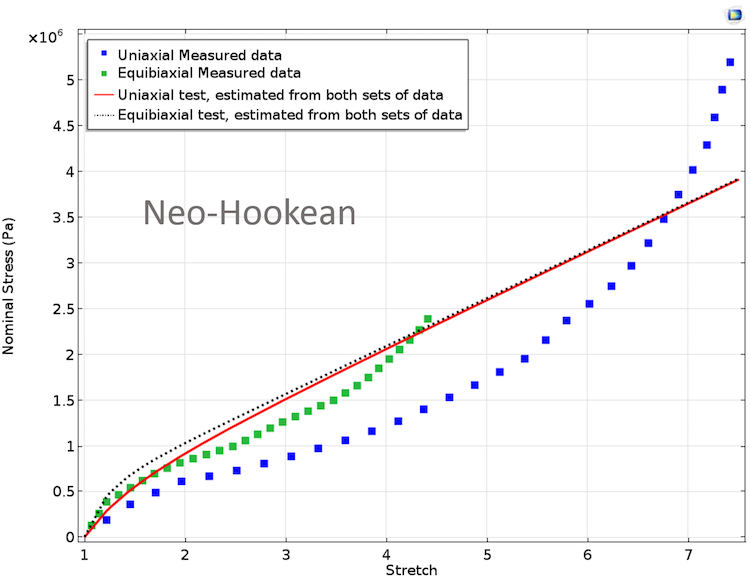
使用 Neo-Hookean 模型拟合的材料参数。为两个测试数据指定同等权重。
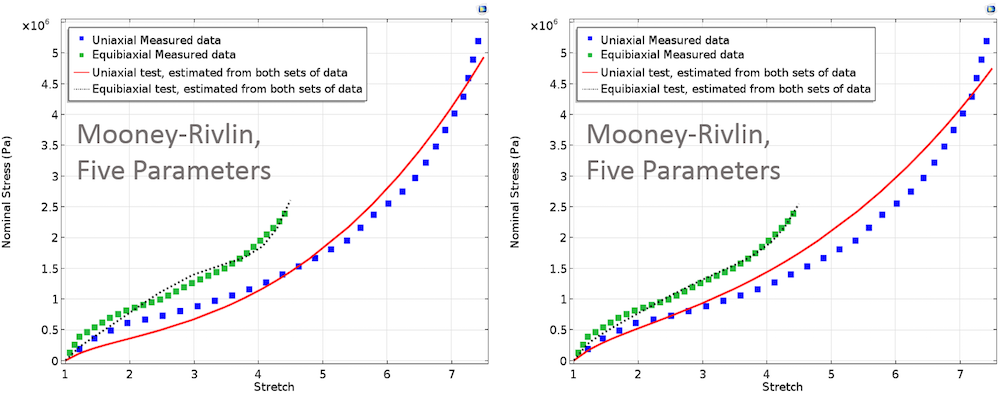
为两个测试指定不等权重并拟合参数,此时将得到一个略微不同的拟合曲线。与 Neo-Hookean 模型类似,我们将建立一个对应于 Mooney-Rivlin、Arruda-Boyce、Yeoh 和 Ogden 材料模型的全局最小二乘目标。我们在下方的计算中先后分析了同等和不等权重的情况。
在不等权重下,我们将在整个双轴数据集中使用一个更高的任意权重。同时,您还可以只针对特定而非整个拉伸范围应用不等权重。此时,我们可以通过为每一个拉伸范围设定单独的全局最小二乘目标特征,从而将具体测试案例分为几部分,进而在不同的拉伸范围应用不同的权重。
下图为不同材料模型在这两个测试下得到的拟合曲线,分别采用同等与不等权重。

左:使用 Mooney-Rivlin、Arruda-Boyce 和 Yeoh 模型的拟合材料参数;为两组测试数据指定了同等权重。右:使用 Mooney-Rivlin、Arruda-Boyce 和 Yeoh 模型的拟合材料参数;为双轴测试数据指定了更高的权重。
当为两组测试指定同等权重时,包含三项的 Ogden 材料模型对两组测试数据的拟合非常好。
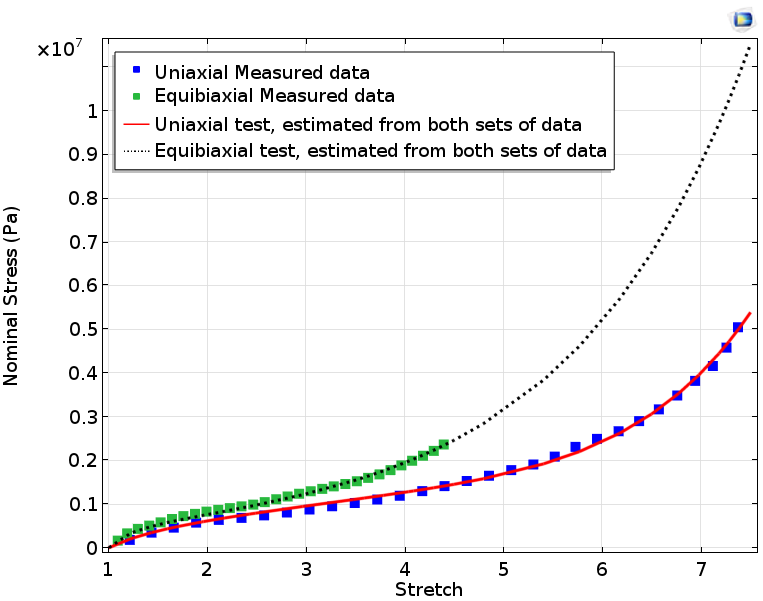
使用包含三项的 Ogden 模型拟合材料参数。
如果只拟合单轴数据,并使用计算参数针对实际双轴测试数据绘制双轴应力,将得到下图所示的结果。图片显示计算与测量双轴应力之间存在不匹配。在材料参数估计中,最好能结合不同的大变形模式执行曲线拟合,而非只使用一种变形模式。
结束语
拟合解析曲线也许是找出超弹性材料模型中材料参数的不错方法;但还应考虑给定超弹性材料模型的稳定性。我们通常采用 Drucker 稳定性准则来确定材料的稳定性。根据 Drucker 准则,与增量应力相关的增量功总应大于零。如果违反了该准则,材料模型将不稳定。
我们在博客中演示了如何使用 COMSOL Multiphysics 的优化接口实现多个数据集的曲线拟合。在 “利用 COMSOL Multiphysics 拟合实验数据曲线” 博客中,我们还讨论过另一种不需要优化接口的曲线拟合方法。通过类似我们这里使用单轴和双轴拉伸数据来估算材料参数的做法,您还可以将测量数据拟合到剪切和体积测试中,以表征其他变形状态。
有关利用优化接口执行曲线拟合的逐步介绍,请查看我们 App 库中的 Mooney-Rivlin 曲线拟合教程。






评论 (1)
ZHENGYI HAN
2018-12-13您好,感谢您的介绍。我注意到blog中介绍的是基于单轴或双轴拉伸数据进行参数拟合。我的问题是,基于拉伸测试数据拟合的材料参数是否同样适用于模拟超弹体在压缩中的形变(例如密封圈的形变)。
谢谢。
韩正一