假设你正在模拟这样一种情况:载荷横跨不同网格单元和边界移动。如果你希望只对一部分几何边界或只在特定条件下施加边界条件,该怎么处理?在这篇博客中,我们将讨论如何利用 COMSOL Multiphysics 灵活处理这种特殊情况。
边界条件的分类
对偏微分方程进行数学处理时,会碰到三种边界条件:狄利克雷、诺伊曼和罗宾。狄利克雷条件用于指定要求解的变量;诺伊曼条件用于指定通量,也就是因变量的梯度;罗宾条件结合了前两类边界条件,用于指定变量及其梯度之间的关系。
下表列举了这三种边界条件在一些不同物理场中的应用示例,以及对应的物理解释。
| 物理场 | 狄利克雷条件 | 诺伊曼条件 | 罗宾条件 |
|---|---|---|---|
| 固体力学 | 位移 | 牵引(应力) | 弹簧 |
| 传热 | 温度 | 热通量 | 对流 |
| 压力声学 | 声压 | 法向加速度 | 阻抗 |
| 电流 | 固定电势 | 固定电流 | 阻抗 |
在使用有限元方法时,这三类边界条件会对所求解问题的矩阵结构产生不同的影响。
诺伊曼条件
诺伊曼条件是“载荷”,位于方程组右侧。在 COMSOL Multiphysics 的方程视图 中,这类边界条件显示为弱贡献。诺伊曼条件纯粹是方程组右侧附加的贡献,因此包含以下变量的任何函数:时间、坐标或参数值。
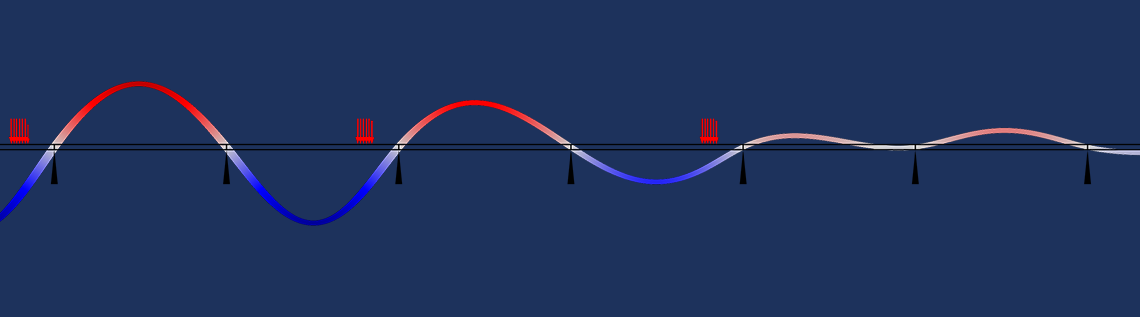
我们来看一个传热问题示例。在这个示例中,半径为 R 的圆形热源沿 x 轴方向以速度 v 移动。其强度呈抛物线分布,峰值为 q_0。该载荷的数学描述为
很明显,移动载荷不可能有域边界,甚至不可能存在一个始终适合载荷分布的网格。
我们可以在该表达式中直接输入载荷分布。因为有两处会用到径向坐标变量 r ,所以将其定义成变量是一个不错的想法。该移动热源的完整输入如下图所示。
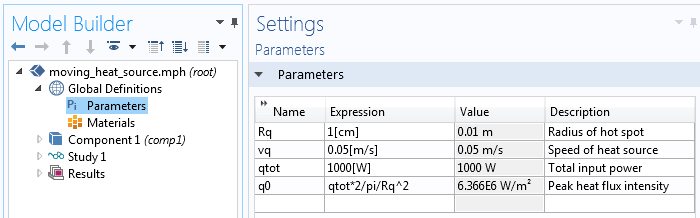
描述移动热源的参数。
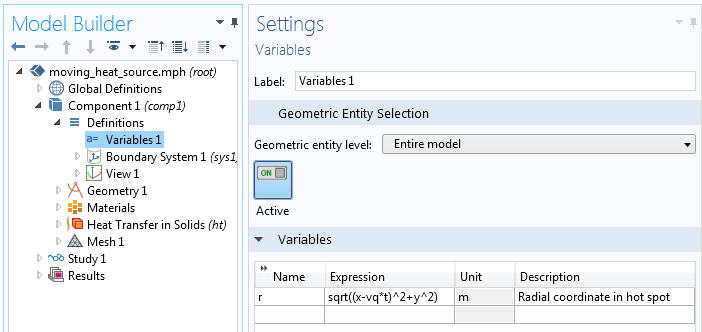
描述从移动热源的当前中心触发的局部径向坐标的变量。
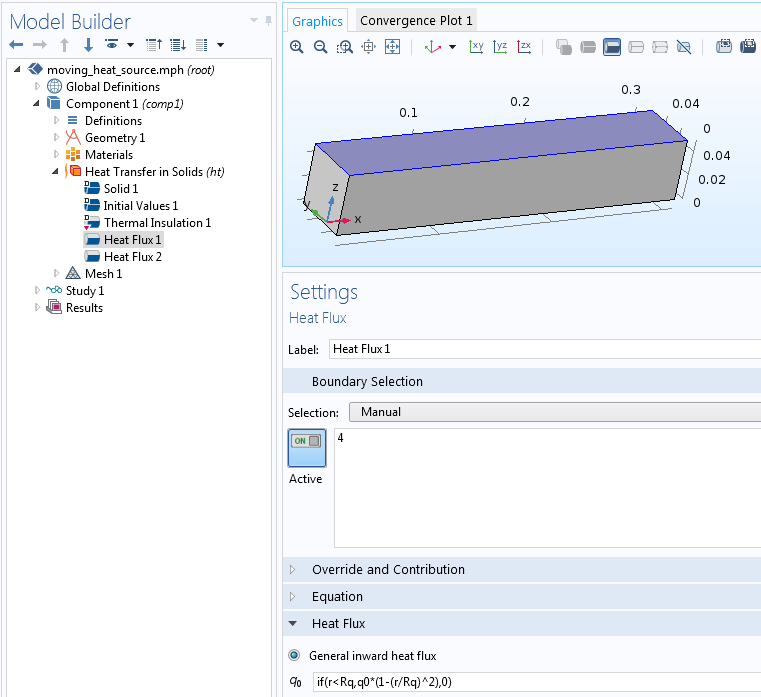
输入热通量。
下方动画显示的是采用上述数据进行瞬态仿真后的结果。假设该问题关于 yz 平面对称,那么载荷实际上被施加到一个半圆形移动热源上。
热源沿块移动时的温度分布动画。
狄利克雷条件
给定狄利克雷条件意味着指定了因变量,所以无须求解因变量。我们可以从问题中删除这类自由度方程。因此狄利克雷条件会改变刚度矩阵的结构。在 COMSOL Multiphysics 的 方程视图 中,这类条件将显示为约束。
假定要将移动点的温度指定为 450 K,这或许有点刻意,但这能表现出诺伊曼条件和狄利克雷条件之间的一个重要区别。假如要添加一个温度 节点并输入一个类似的表达式( if(r < R,450[K],0)),这意味着没有被热源点覆盖的那部分边界的温度将被设定为绝对零度。
不过,我们的目标是在热源点之外停用狄利克雷条件。为此可以使用一个小窍门:如果将if(r < R,450[K],ht.Tvar) 作为指定值输入,就能实现目标(如下方动画所示)。
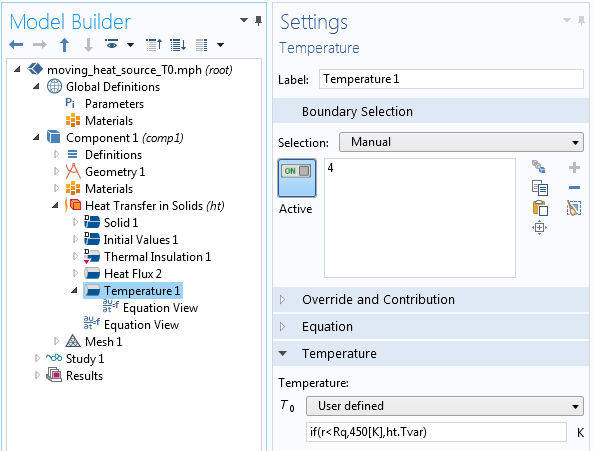
含条件约束的狄利克雷条件设置。
指定温度的热源点沿块移动时的温度分布动画。
为了理解其运行原理,我们启用了方程视图,来查看狄利克雷条件的实现(本示例中为指定温度):
启用 方程视图。
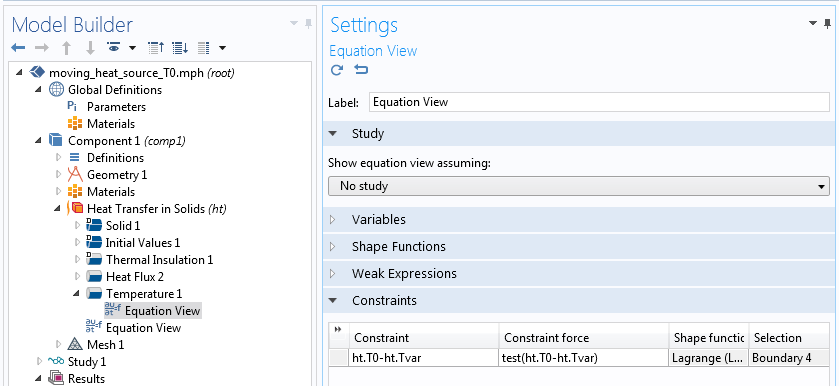
方程视图中的 温度节点 。
约束用公式表示为 ht.T0-ht.Tvar,代表ht.T0-ht.Tvar = 0。第一项是作为输入的指定温度。第二项是转换成变量的温度自由度。这个约束使温度等于给定值,除非给定值恰好是ht.Tvar 。如果发生这种情况,符号代数在分配过程中会将表达式简化为 ht.Tvar-ht.Tvar,并进一步计算为零。当约束表达式为 0时,表示没有约束。
弱约束
在 COMSOL Multiphysics 中,狄利克雷条件实际上有两种可能的实现方式:默认情况下为上文提到的逐点约束,还可以使用弱约束。在弱约束中,我们要添加方程,而不是移除方程。热通量需要被添加为额外的自由度(拉格朗日乘子),以强制指定温度值。
只要对上面的温度表达式稍作更改,就可以使用本质上相同的小窍门使弱约束含条件限制。要使用弱约束,必须先启用 高级物理场接口选项。
启用 高级物理场接口选项。
在物理场接口内对某个节点选中弱约束后,就会为拉格朗日乘子添加额外的自由度。这个示例中,该自由度名为 T_lm。
如果应用了上文中的温度表达式,那么在停用狄利克雷条件的边界部分,额外的自由度不会得到任何刚度矩阵的贡献,因此刚度矩阵变为奇异矩阵。为了避免这种情形,我们将 if(r < R,450[K],ht.Tvar) 更改为 if(r < R,450[K],ht.Tvar-T_lm*1e-2)。不同的模型和物理场,用于 T_lm 的乘子也不同,因此可能需要进行一些调整。
至于其中的工作原理,我们会像教科书中一样“作为练习留给读者”。
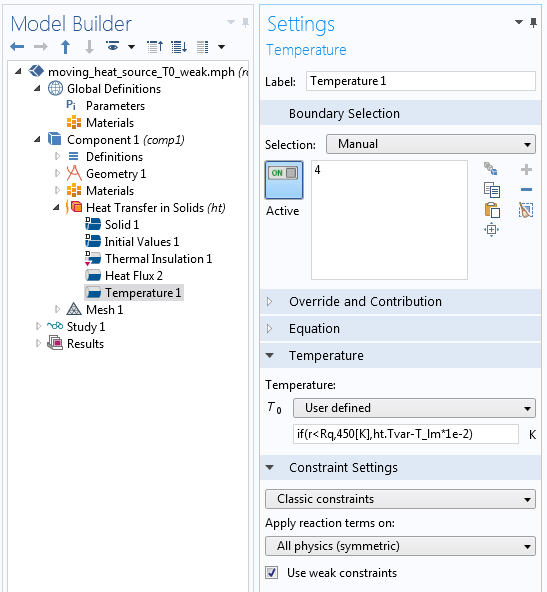
使用弱约束时,含条件限制的狄利克雷条件设置。
罗宾条件
罗宾条件通常对刚度矩阵和方程右侧都会造成影响。虽然刚度矩阵的结构不会受到影响,但会在现有位置上的值添加值。在方程视图 中,罗宾条件同样显示为弱贡献。将这类条件转换为关于时间、空间和其他变量的函数与使用诺伊曼条件时的做法一致。
不过有趣的是,选择合适的值确实可以转换罗宾条件,使之近似为狄利克雷条件或诺伊曼条件。如果模拟过程中你希望在这两类边界条件之间切换,那么这一点十分重要。
要创建狄利克雷条件,需要对“刚度”指派一个高值,例如弹簧常数或传热系数。在数学术语中,这实质上是狄利克雷条件的 罚 实现。刚度越高,自由度的指定值就越精确。但这里需要注意:刚度过高会影响刚度矩阵的数值稳定性。而在传热问题中,要选择“高”的传热系数 \alpha,起始值可以是
其中, \lambda 表示导热系数,h 表示特征单元尺寸。
用适当的材料属性(也就是固体力学中的杨氏模量)替换 \lambda,就可以在其他物理场实现相同的计算。将因子设为 1000 只是一个建议,您也可以替换成 104 或 105。
如果要使用上一个对流模拟示例中的移动温度为 450 K 的热点,则可以采用下图中的设置。表达式中使用了单元大小的内置变量 h 。
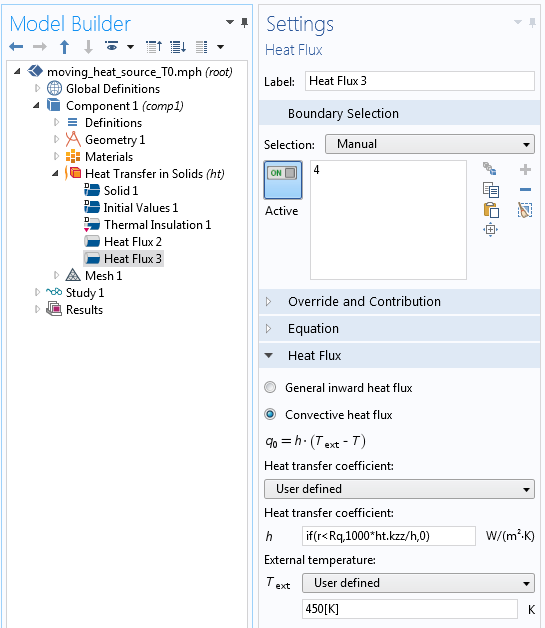
利用对流条件指定温度。
我刚开始使用有限元分析时,有时无法在结构力学的有限元程序中指定非零位移。这一限制是由于编程越来越复杂造成的。遇到这种情况时,最佳方法是添加预变形的刚性弹簧来使用罚函数法。但是刚度不能过大,因为那时还在采用单精度运算!
下面,我们来讨论近似为诺伊曼条件。我们希望热通量与表面温度无关。在这个传热示例中,罗宾条件表明向内热通量 q 为
其中, \alpha 表示传热系数,T 表示边界温度,T_{\textrm{ext}} 表示外部温度。
所以,如果 T_{\textrm{ext}} 比表面预期温度高很多,那么 q \approx \alpha T_{\textrm{ext}}。这时就是选择一个任意大的 T_{\textrm{ext}},然后计算一个合适的传热系数,如下图高亮处所示。
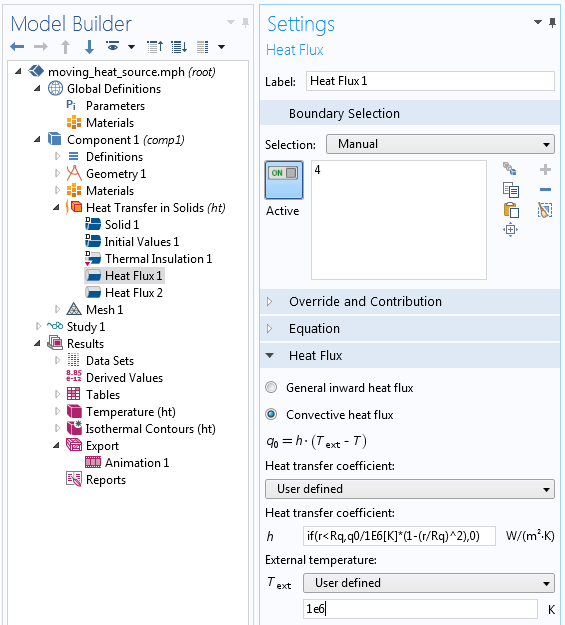
利用对流条件指定热通量。
在实际情况中,设计人员利用这个原理在一个实际机械组件引入了一个固定力:一根预应力的又长又软的弹簧。如果弹簧的预变形远大于与弹簧连接部件的位移,则弹簧的力几乎保持不变。
解决离散误差
当边界条件受制于布尔表达式(类似 if(r < R,...)时,施加了此边界条件的区域边界很可能不会跟随网格单元的边,这将引入离散误差。
使用诺伊曼条件或罗宾条件时,要对每个有限元进行数值积分,并计算该单元中大量离散高斯点的函数值。如果网格单元的大小大于载荷的几何大小,那么施加有载荷的确切高斯点数会显著影响总载荷。由此,施加有载荷的小块区域上应该总是存在几个单元。
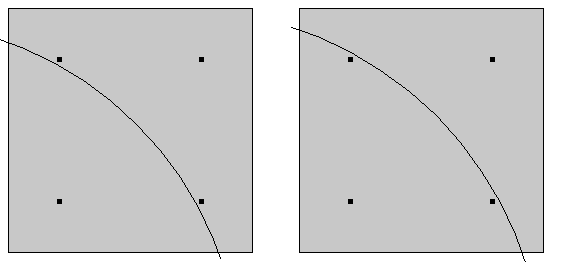
载荷位置稍微移动一点就可能改变所含积分点的数量。(在实际情况中,改变的积分点数会更多。)
因此,至少从离散点的意义上讲,要对网格节点施加狄利克雷条件。下图显示,在模拟指定温度为 450 K 的圆形点的移动时,某一时间点上的温度分布和热通量。在热点的前端,一个温度为 260 K 的暗影清晰可见。由于模拟的初始温度和环境温度均为 293 K,因此这一暗影不应出现。出现这一数值差异,是基于这样一个事实:并非每个单元上的所有节点都设定了狄利克雷条件。在狄利克雷条件的不连续性处,就会出现奇异点。这一话题我们在上一篇博客中探讨过。细化网格可以减少这类问题发生。
下图中的绿色箭头表示指定温度后产生热通量的节点。模型中的网格密度太小,使得近似半圆变得相当困难。
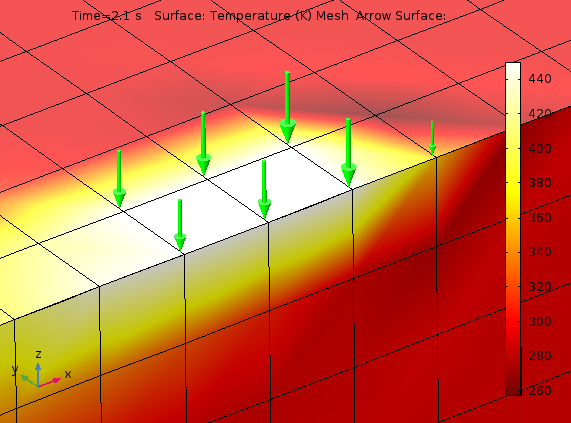
指定温度的半圆周围的温度分布和热通量。
边界条件中解的依赖性
要将解作为边界条件的输入有多种方法。这样做往往会引入非线性,但COMSOL Multiphysics 可以自动检测到非线性。
我们以一个梁为例。梁的下方有一个支撑,其作用是在梁发生一定挠曲后阻止梁的进一步移动。在 梁 接口的 指定位移/旋转 节点中,设置一个含条件限制的狄利克雷条件可以实现模拟。

具有挠曲、控制支撑和分布载荷的梁。
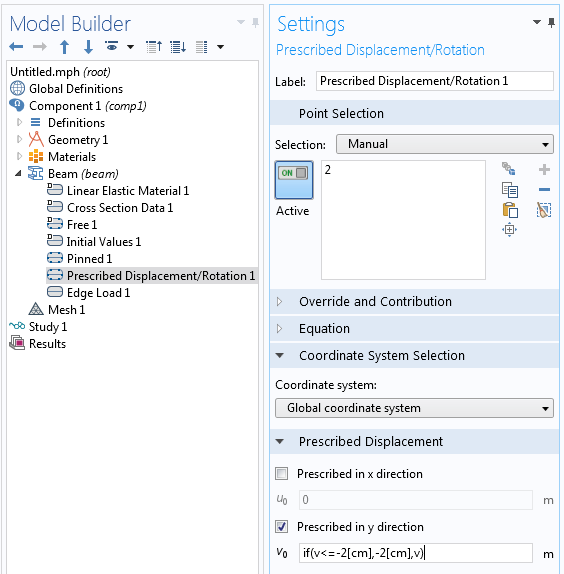
指定梁应在挠曲为 2 厘米时停止移动的设置。
分析表明预期的梁行为发生了。当载荷较小时,挠曲形状呈对称结构,而载荷较大时,梁上受额外支撑的点会停止移动。载荷达到最大时,梁上的曲率甚至会由正值变为负值。变形图可以显示这一变化,不过弯矩图中更加明显。
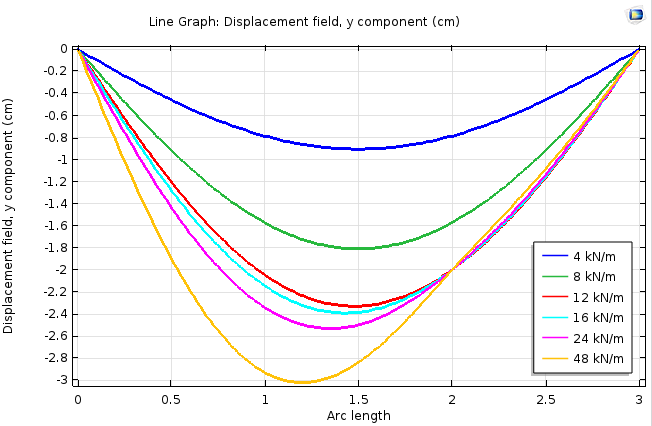
在支撑点处移动 2 厘米后停止的梁位移。
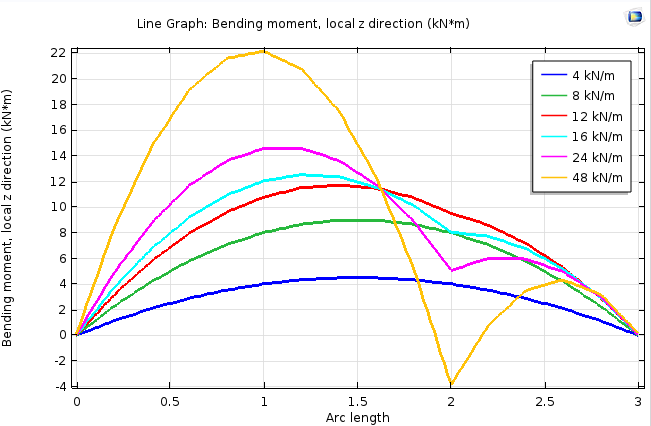
载荷不同时梁上的弯矩。
文中重点讨论的方法其实还相当不成熟,而且迭代解的收敛特性可能还不够好。更可靠的实现方式是在支撑点处使用高度非线性弹簧,由此反作用力就是关于位移的连续可微函数。这种做法实际上相当于在 固体力学 接口中实现罚接触。
在 COMSOL Multiphysics 中使用边界条件的结论和思考
COMSOL Multiphysics 允许您访问各种强大的原理,用于指定非标准边界条件。今天,我们只讨论了几个使用这类条件的案例。
如果你对分析含有移动载荷的模型感兴趣,请查看 COMSOL App 库中的移动载荷教程模型。
如果你在模拟过程中对于如何指定非标准边界条件有其他问题,请立即联系我们。




评论 (46)
恭正 陈
2018-11-13comsol怎么模拟一个正方形的不稳定性运动?
恭正 陈
2018-11-13请教下COMSOL如何模拟正方形的不稳定运动?
Hehua Xu
2018-11-15在求解地球上的区域热结构的问题中,通常是已知表层的温度,同时通过测试也可以知道表明的热流(热通量),而某个深度的温度和热流都未知。在选定求解区域后,最好的办法是在上边界同时加载温度和热流边界,但软件中无法实施,不知专家有什么建议。谢谢。
Yong Jiang
2019-03-14不同的物理场,如何选择合适的节点?
Haili Wang
2019-04-15Hehua ,您好!
感谢您的评论。
对于您的问题,建议您联系系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
Haili Wang
2019-04-15Yong Jiang ,您好!
感谢您的评论。
您的问题有点过于笼统,建议您将问题细化之后,联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
义奎 温
2019-06-06关于动载荷的施加和变化的电场是否计算没有太大的差别呢
Jiawei Kao
2020-01-29您好!comsol在固体力学中,建立了较为复杂的几何模型后,在选择其中一些边界施加相应条件时,发现这些边界的相应编号不是按着建模顺序的前后进行赋予的,请问这个有没有相关的详细说明?
Jing Yuan
2020-07-12是否有人可以解释一下,这里面洛平边界条件是否对应的是 k*dT/dx=T0-T 这种边界条件?我的问题是,如何在Comsol中设置形如 k.dT/dx=T0-T这样的边界条件呢?我尝试用convective heat flux, q0=h(Text-T), 可是计算结果q0和conductive heat flux (k*dT/dx) 并不相等,这是为什么呢?谢谢
翀 施
2020-07-13 COMSOL 员工洛平(罗宾)边界条件在COMSOL的传热模块中对应的条件应该是-k*dT/dx=h*(T0-T) ,需要添加一个负号,另外这个表达式是相对与1D模型而言,如果是二维甚至是三维还存在T关于y和z的梯度项。COMSOL中的convective heat flux, q0=h(Text-T),就是一个现成的洛平(罗宾)边界条件。
hang zhang
2020-09-21请问我的激光光源是条状的不是圆形的,我该怎么定义条状的激光光源
Ying (Grace) Xu
2020-09-24感谢您的评论。
定义条状的激光光源需要有描述条状光源强度分布的数学表达式,然后替换博客中圆形强度分布的表达式。
如还有其他问题联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
shelly 赖
2021-05-10请问用comsol如何得到方形板四周受均布压力时的位移云图。总是会提示相对误差(7.4)大于相对容差。comsol中有像ansys中的弱弹簧平衡微小力的设置吗?
Yang Zhang
2021-05-11 COMSOL 员工您这是由于模型欠约束导致的报错,您可以在边或域上添加“弹簧基础(spring foundation)”实现其平衡。
shelly 赖
2021-05-13你好,请问如果在四周受压的方形板中间挖一个洞,并给定洞的边界上的点的位移,计算结果显示方形性板四个角的位移极大且超出合理范围。如果只指定洞的边界的位移,计算结果合理。若是加上四周的面力,四个角的位移极大。请问这个要怎么处理?
Lei Cao
2021-05-19 COMSOL 员工shelly 赖, 您好!
感谢您的评论。
仅凭描述无法准确判断您的问题,目前猜测可能是施加的力的量级存在问题,也就是设置的力过大。或是对于大变形问题未考虑几何非线性,计算都按照线弹性材料模型进行考虑。
建议您将问题和相关模型发送至COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
柳春 杨
2021-05-17我想请教一下边界条件怎么设置不会反弹超声波
Lei Cao
2021-05-19 COMSOL 员工柳春 杨, 您好!
感谢您的评论。
您指的应该是声波的反射。在材料声阻抗变化的边界上都会产生一定的反射情况。针对不同的建模情况有不同的设置方式,可尝试辐射边界、阻抗边界、完美匹配层、低反射边界(固体瞬态)等方式。
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
Yuxi Zhang
2021-09-24您好,请教下:无限大的空间,建模时只截取有限空间(比如一立方体)进行仿真,那如何在立方体的边界设置连续边界条件呢?及立方体内的物理量=立方体外的物理量。 谢谢
Liwen Yang
2021-09-27 COMSOL 员工您好,截取无限域的有限空间进行有限元仿真,对于截断区域有三种处理方法:无限元、完美匹配层、吸收层。对于不同类型的问题需要选择不同的处理方式,详细内容可以参考:http://cn.comsol.com/support/knowledgebase/1272 。
xiaoling chen
2023-03-20高压可压缩流体的入口条件如何同时设置为压力和速度边界条件?
越 赵
2023-03-22 COMSOL 员工您可以使用高马赫数流接口中的入口边界条件来设置,压力体现在入口静压上,速度可以转换为马赫数进行边界设置。
Liang Cheng
2023-05-03您好,请问一个三维的桥,如何在桥面上设置移动载荷仿照车辆经过呢
Yuhong Zhang
2023-05-17 COMSOL 员工您可以通过一组载荷脉冲来模拟桥上面的车辆,通过改变载荷脉冲的速度和间距等参数来模拟不同的车速或者是车距等。详细内容您可以参考案例:https://cn.comsol.com/model/beam-with-a-traveling-load-20401
泽昊 李
2023-05-25如何在二维模型外建立一个由面外热源控制的温度场与二维模型换热
Haoze Wang
2023-06-30 COMSOL 员工您好,建议使用面外热通量边界条件,设置二维面上侧或下侧的向内热通量。
泽昊 李
2023-07-24面外热源是由一个能量方程控制的温度场,面外热源的大小与二维平面的域相同,应该如何设置
闯 薛
2023-07-18请问如果我想设置一个热源的热流密度随某一形状递减,该怎么设置呢?例如一个直线但是上面热源分布不是均匀的,是从左到右逐渐递减的,这个要用到移动载荷吗
Yi Fan Wang
2023-08-23 COMSOL 员工您好,您可以将热源乘一个有关于x(关于位移的变量)的函数就可以。
燕 毛
2023-08-22请问为什么在COMSOL的模型上添加端盖面后无法选中端盖面作为空气入口边界?
Yi Fan Wang
2023-08-23 COMSOL 员工您好,您需要确认您加完端盖面以后,能否形成封闭的流动域。
绮 漆
2023-08-28老师您好,我现在遇到一个很基础的问题,在使用达西定律和理查兹方程模块时,怎么设置某边界条件为自由呢?一直没有找到这个选项。
Haoze Wang
2023-08-30 COMSOL 员工您好,建议设置水头或使用透水层边界条件。
绮 漆
2023-09-02好的老师,谢谢老师,还有一个问题,我现在需要在边坡顶部0-60min内加一个质量通量,底部和侧面设置的无流动,坡面和坡脚设置的透水层,重力作用下的压力作为初始值,但是一直报错说找不到一致的初始值,最后一个时步不收敛,这个问题是出在边界条件还是哪个接口呢?
Haoze Wang
2023-09-04 COMSOL 员工您好,请参考求解初始值不一致的瞬态模型的解决方法:https://cn.comsol.com/support/knowledgebase/1172
绮 漆
2023-09-05谢谢老师,我之前看过了,用了分步和阶跃函数的方法,还是没有解决,不知道是否是跟边界条件有关。另外请问老师6.0版本里,使用达西定律接口下非饱和多孔介质,和直接使用理查兹方程有什么区别吗?
Haoze Wang
2023-09-06 COMSOL 员工您好,建议您将模型发送至技术支持中心:https://cn.comsol.com/support,由工程师具体分析您遇到的问题。达西定律接口下的非饱和多孔介质节点使用的就是理查兹方程。
荟鹏 王
2023-09-15固体力学中怎么添加力臂平衡条件
Anran Wei
2023-09-20 COMSOL 员工您好,在计算物体变形时每个点上的应力、应变时,会自动考虑各个点上的力平衡与力矩平衡,固体力学的基本控制方程就已经考虑了这一点。您需要添加的边界条件,都可以转化为边界某处位置上的载荷(“边界载荷”条件)或位移(“指定位移”条件)。
Chen Li
2023-09-21老师,您好!我想问一下,稀物质传递物理场的。就是离子浓度c1在整个计算过程中是变化的,不同区域的c1离子浓度不同,但是定义的边界条件是有关于c1离子浓度的表达式(指定是改表面与溶液界面的c1离子浓度)。请问老师这种情况的边界条件可以设定吗?如果可以,要怎么设定呢?
Qihang Lin
2023-09-25 COMSOL 员工可以将表达式设置为与时间相关、空间相关的函数。软件内置的时间相关的变量为t,空间相关的可能是x,y,z,您可以用这些变量来设定函数关系式
瑾嵘 方
2023-11-08老师您好,请问comsol一根管的进口温度如何设置成计算后另一根管的出口温度
Haoze Wang
2023-11-10 COMSOL 员工您好,可以使用两个管道传热接口,分别计算两根管的温度场,在其中一个接口的入口温度设置处引用另一个接口的因变量即可。
Jing Guo
2023-12-05请问在用有限水域模拟无限水域时,有限水域的边界条件应该如何设置才能实现低反射或者无反射?
Min Yuan
2023-12-05 COMSOL 员工关于无限区域的模拟一般可以通过无限元域、完美匹配层、吸收层三种方式实现,不同方式的具体适用场景可以参考下列介绍:http://cn.comsol.com/support/knowledgebase/1272
峰 陈
2023-12-12您好!请问如何在移动的边界上添加边界条件,比如用水平集确定的油水界面上添加边界条件,谢谢