如何模拟消声覆盖层

海豚和蝙蝠在数百万年前，便已经拥有了通过回声进行定位的能力；然而直到二十世纪初，人类才发明出了声纳装置。不久之后，首款声呐对抗装备——消声覆盖层——随即应运而生。今天，我们将介绍如何借助 COMSOL Multiphysics® 来模拟消声涂层的回声消减效果。此类建模技术同样适用于穿孔板、声子晶体，以及其他各类具有周期性结构的消声装置。

消声覆盖层

二战时期，德国海军为了避免被声纳探测到，在大块的橡胶布上钻出均匀分布的小孔，并将其覆盖在 U 型潜水艇表面。虽然具体工艺细节不断进步，但这种基于在阻尼层中嵌入周期模式的技术仍在使用中。人们期望在特定频率范围内最大限度地消减回声，然而要找到符合要求的模式和材料属性却是一件棘手的任务。借助建模技术，一切都会轻松许多。

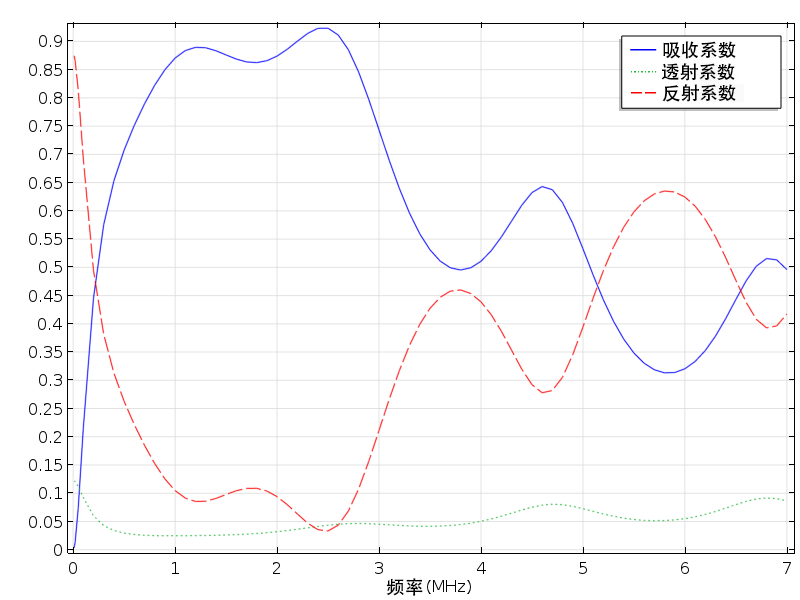
我们选取了参考文献 1 中讨论的覆盖层，来向您演示如何使用 COMSOL Multiphysics® 软件建立消声涂层的模型。作者在文中介绍了一种PDMS（聚二甲基硅氧烷）薄膜，中间嵌有圆柱形孔的二维阵列。薄膜覆盖在潜艇外壳上，小孔朝向钢板。当潜水艇浸没在水中时，小孔内便会产生气泡。尽管覆盖层的厚度仅为 0.2 mm，但是对于 1~2.8 MHz 范围内的大多数频率而言，可将反射率降低到 10％ 以下；针对高达 5 MHz 的频率，也能减少将近 50% 的反射率。

寻找最小的单元格

在对周期性几何结构进行建模时，首先需要分析出如何尽量的减小几何结构尺寸。下图显示了空气腔的周期性分布。蓝色的虚线方框表示随机选取的普通单元格。由于应用了周期性Floquet 边界条件，因此几何结构适用于任意角度声波入射。如果您想详细了解周期性结构上倾斜入射示例，请参阅“案例下载”中的多孔介质隔音设备模型。

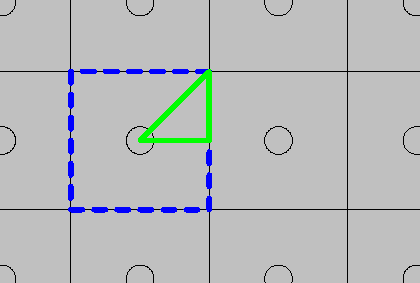
周期模式的顶视图，其中包含了两个完整的单元格。

假设平面波垂直入射，这样就能同时利用周期性和几何的镜像对称性。在建立完 x- 平面和 y- 平面对称后，往往很容易忘记还有一个镜面平面，该平面与 x 轴和 y 轴均呈 45 度角。完成上述步骤后，就获得了上图中用绿色实线表示的三角形结构，它占据了全周期单元格的 1/8。有一点请注意：未使用对称性并不会造成大的影响，只是会增加模型的运算成本而已。

将几何结构截断

下图为我们创建的几何模型，可以看出 PDMS 的上方是水、下方是钢：

在 COMSOL Multiphysics® 中使用附加的 “声学模块”生成的几何模型。

接下来，我们将模型中钢与水设定为会无终止地超出模拟的几何结构。显然，水是一个非常理想的假设，但钢似乎并非一个非常好的选择；这是因为潜艇外层的非耐压壳体可能只有几毫米厚，忽略的船壳体的另一侧意味着忽略了壳内部可能发生的任何反射。

然而，由于 PDMS 和钢的声学阻抗相差很大，所以穿过钢材料中的声波很少。同时，大部分反射的声音会被覆盖层吸收掉。因此，添加钢域的完整厚度就留给有兴趣的读者自己练习。如果您有意尝试，请在留言区告诉我们！

模拟“无限大”的材料时，可以利用多种不同的低反射边界条件或者完美匹配层（perfectly matched layer，简称 PML）。低反射边界条件最适合处理假设平面波是垂直入射；而 PML 的优点在于适用范围更广，这也使其成为了处理非周期性、开几何的最佳选择。如希望了解更多有关 PML 的信息，请阅读介绍用于电磁波问题的完美匹配层的博客文章，这篇文章中的关注点和结论与本文讨论的压力声学和结构力学内容相似。

衍射

那么，我们可以假设只有垂直的平面波入射到了几何模型的顶端吗？要弄清这一点，我们需要简要学习一下衍射理论。

由平面波入射在周期性结构上时会引起透射波和反射波，二者可以被描述为以有限数量的离散衍射角进行传播的平面波的总和。虽然紧邻周期性结构的区域中也存在一些任意形状的瞬逝场，但是传播波都是平面波。

通常，大部分声能最终将归于“零级衍射”，这实际上就是入射波的折射波和镜面反射波。当两个相邻单元声波的声程差是波长的整数倍时，该反射角度上会生成更高衍射级数的反射波。描述此现象的公式为

其中，m 表示衍射级数，其值可取 0，± 1，± 2……；c_i 表示入射介质中声波的速度；f 表示频率；d 表示重复单元的宽度；θ_i 表示入射角；θ_r,m 表示第 m 级衍射波的反射角。

同样地，透射衍射级数的方程为

其中 c_t 表示最终介质中压力波的波速，θ_t,m 表示第 m 级衍射波的透射角。

现在，让我们来想一想当 θ_i = 0 时的消声涂层模型。若要保证第 m 级的反射衍射波发生，必须满足以下条件

所以，如果 c_i/(fd)>1，则衍射波不会发生反射。同样地，若 c_i/(fd)>{c_i/c_t}，则衍射波不会发生透射。由于钢中的声压速度高于水，因此反射波会最先发生衍射。当 d =120μm 且 c_i = 1481 m/s 时，我们可以得出以下结论：在低于 12.3 MHz 的频率下，衍射将不会发生。

建立消声覆盖层模型

既然确认了相关频谱不需要 PML，那么我们只需将模型中的水和钢设置得足够深，便可使大部分消散波无法到达外部边界。至于边界条件，我们对钢域应用了低反射边界，对相应的压力声学域，即水域，应用了平面波辐射。

压力声学 接口非常适合用于模拟水和空气腔的内部。当模拟微小的密闭空间时，热粘性声学 接口能提供更加精确的结果，然而这仅适用于当热边界层和/或粘性边界层具有显着厚度的情况。而在这里我们关心的频带内，这些层仍然比空腔的尺寸薄的多。

此外，我们还使用了固体力学 接口来模拟钢域和 PDMS 域。如果在 COMSOL Multiphysics® 的模型向导 中选择声-结构相互作用，频域，软件将生成对应的两个接口，同时还包含一个自动关联的声-结构边界。

将垂直入射的入射压力场添加到平面波辐射条件中，即可激发模型。为了得到透射系数、反射系数和吸收系数，您需要分别获得透射的能量、反射的能量、吸收的能量各自的占比。

透射功率十分容易计算。外部机械能通量表示为 solid.nI，可实现自动计算，您只需在钢域的低反射边界上对其积分。由已知的平面波入射功率解析式得到入射功率，用 solid.nI 除以入射功率，即可推导出透射系数。

净声学强度是一个矢量（acpr.Ix，acpr.Iy，acpr.Iz）。计算反射能量的步骤是，用入射功率减去声强 z 分量负值在入口处积分，再除以入射功率，即可获得反射系数。最后，由于三个系数总和为 1，于是就能非常方便地计算出吸收系数。

结果

下图显示了透射系数、反射系数和吸收系数的计算结果，与文献（见文末）中的结果基本一致。

更多资源

• 查看其他具有周期性几何特征的声学模型和 App：
  • 多孔隔音设备
  • 声波反射分析器
  • 声表面波气体传感器
• 阅读相关博客：
  • 认识并计算穿孔板的转移阻抗
  • 另一篇有关模拟 RF 消声室的博客文章探讨了应用于电磁波领域的其他同类技术

参考文献

1. V. Leroy, A. Strybulevych, M. Lanoy, F. Lemoult, A. Tourin, and J. H. Page: Superabsorption of acoustic waves with bubble metascreens, Phys.Rev. B 91, 020301(R), 2015