如何模拟离子交换膜和唐南电位

离子交换膜广泛应用于电化学工程领域。在聚合物电解质燃料电池和钒液流电池中，它们用于传导离子，同时防止反应物和电子在两个流室之间流动。在电渗析中，促进正电荷或负电荷离子通过的能力也用于从离子中去除水。在本篇博客文章中，我们将探索离子交换膜的离子选择能力。

Nernst-Planck-Poisson 方程

离子交换材料通常作为多孔介质进行建模，这种多孔介质由固定基质组成，其中的孔隙充满水和额外的移动离子。对于任何见过 Nafion® 膜（最常见的聚合物电解质材料之一）的人来说，这听起来是完全错误的。这种材料看起来完全透明、均质，但基质由透明的聚合物主链构成。遇水膨胀的孔隙为纳米级范围。

离子交换膜的关键特征是固定在主链并位于内孔壁上的固定离子。在 Nafion® 示例中，固定离子是 \mathrm
{SO}
_3^- 基团，位于从聚合物主链延伸的聚合物尾部的末端。正如我们将在下面的讨论中看到的，离子交换膜中固定电荷的浓度和符号对于移动离子在膜中的传输至关重要。

泊松方程根据下式将所有电荷的总和与电位相关联

(1)

其中，\phi_l 是电解质相的电位，\epsilon 是介电常数，\rho 是空间电荷密度。

在本例中，我们可以将空间电荷分成移动离子和固定离子

(2)

上式中，F 是法拉第常数；z_i 是电荷；c_i 是移动离子的浓度，其中i 是物质标号，并对所有 N 个离子求和；\rho_\textrm{fix} 是基质中固定离子的电荷密度。

在离子交换介质外的自由电解质中，固定离子的浓度为零，因此 \rho_\textrm{fix}=0 。

为了模拟离子的传输，我们首先将每个离子的电化学电位定义为

(3)

其中，R 是摩尔气体常数，T 是温度，c_{i,\textrm{ref}} 是某个（任意）参考浓度。

假设为稀溶液（即，每个离子仅与周围水分子相互作用），并且只在扩散和迁移情况下发生离子传输，我们根据以下公式基于电化学电位的梯度来定义移动离子的通量

(4)

其中，\mathrm{mob}_i 是迁移率。

固定离子的通量为零。请注意，由于孔隙度和弯曲度效应，我们通常认为膜中离子的迁移率低于自由电解质。但在下面的示例中，我们将忽略这一点。

如果你习惯于 用菲克定律模拟扩散，同样值得一提的是，迁移率和扩散系数是通过 Nernst-Einstein 关系式相关联的

(5)

由于没有离子产生也没有离子消耗，假设为稳态解，因此离子通量的散度为零。

(6)

方程（1）和方程 （6）（每种物质一个）通常被称为 Nernst-Planck-Poisson（NPP）方程组。

用 NPP 方程模拟离子交换膜

我们将 NPP 方程应用于一个简单的问题，研究当我们改变膜中固定离子的浓度时，离子选择能力是如何变化的。

作为一个建模问题，我们使用 100 μm 厚的膜，它被两个长度相同的自由电解质域包围，并位于一维几何结构中。我们模拟了三种离子（A⁺、B^–和 C^–）的传输，我们还将向中间的离子交换膜域添加一个固定电荷。在最左侧和最右侧的外部边界上，浓度和电位是固定的。比如，这个模型可以代表电渗析槽中的一个膜，其中的湍流可确保良好的混合效果，这样，我们可以假设膜各侧扩散边界层外的浓度恒定（见图 1）。

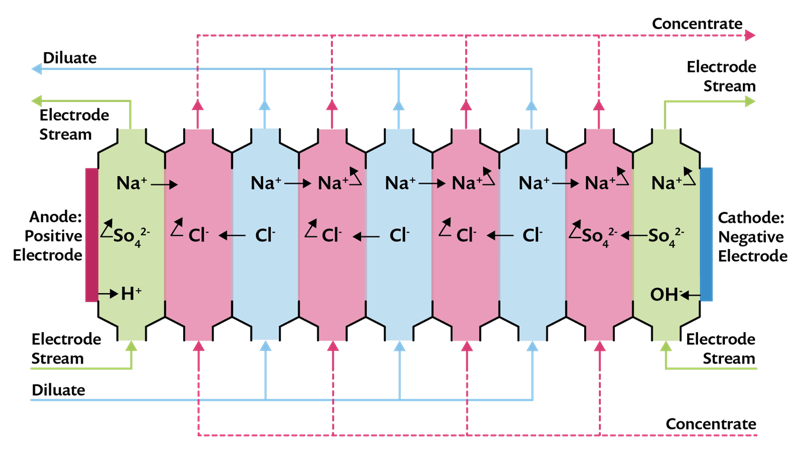
图 1. 用于水淡化的电渗析槽示意图。离子交换膜位于每两个流体室之间。膜的固定电荷的符号交替变化，控制着膜主要允许正离子还是负离子通过。

图 2. 几何结构和边界条件。

在左边界，我们设置\phi_l = 0 V、c_A = 0.1 M、c_B = 0.1 M、c_C = 0。在右边界，我们设置 \phi_l = 0.1 V、c_A = 0.1 M、c_B = 0 M、c_C = 0.1 M。我们将所有离子的迁移率设为相同，将膜中固定离子的电荷设为 -1。

正如我们将看到的，当增加固定膜电荷时，使用 NPP 方程组模拟离子交换膜会导致因变量的梯度越来越大。因此，我们使用稳态求解器，通过将固定离子的浓度从 0 逐步升至 1 M（使用 COMSOL® 软件中的辅助扫描）来解决问题。

图 3 显示当固定离子浓度从 0 到 1 M 变化时，通过槽的每个离子的摩尔通量（从左到右）。不管膜电荷如何，电场的方向都会导致 A⁺向左传输（通量符号为负）。

B^–和 C^–浓度的边界条件决定了这些物质的整体通量方向，但电场的方向解释了为什么 B^–以较快的速率向右侧传输，而 C^–以较慢的速率向左侧传输。当增加膜电荷时，我们可以看到 B^–的通量减少（仔细观察可发现 C^–也是如此）；也就是说，增加膜电荷会导致 B^–和 C^–在膜传递中受到的阻塞力变大。还应该注意的是，阻塞只是部分原因。

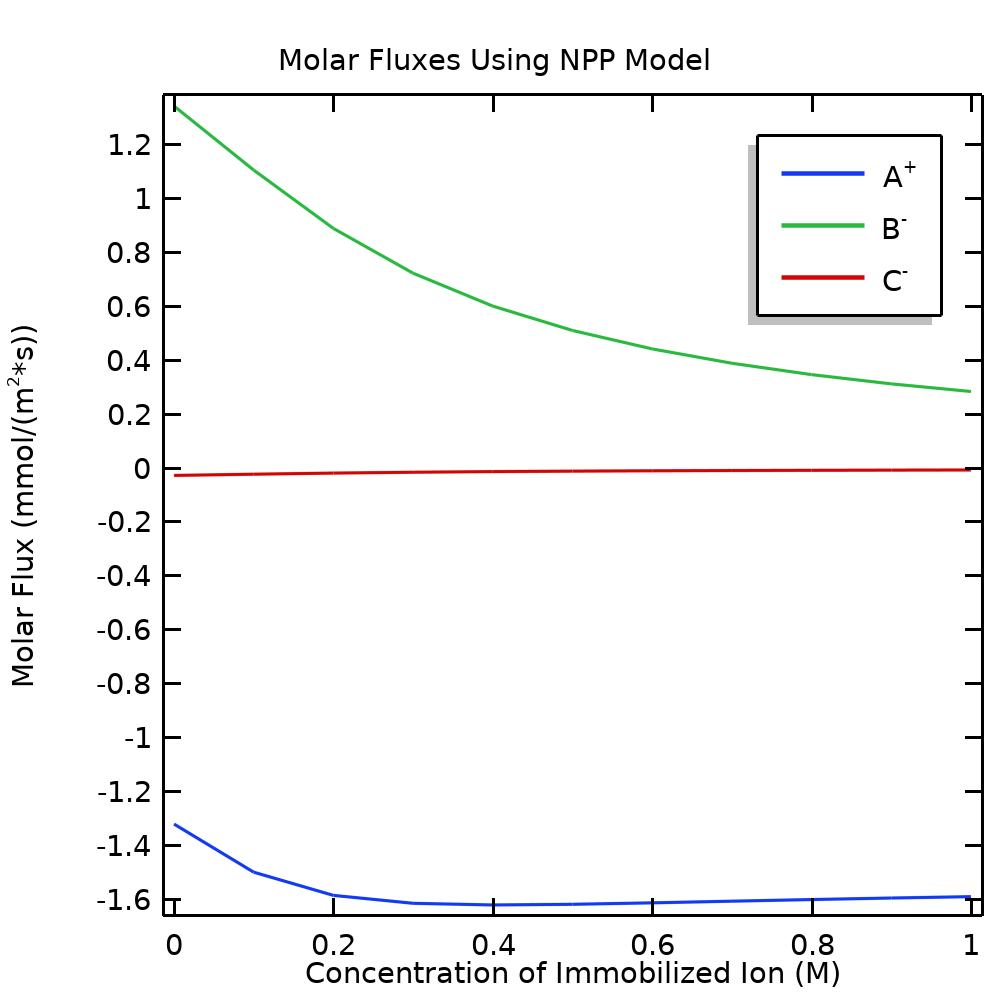
图 3. 当改变膜中固定离子的浓度时，NPP 模型中移动离子穿过槽的摩尔通量。

图 4 中绘制的 NPP 问题的浓度图揭示了阻塞效应解释中的关键部分。膜中 A⁺的浓度高于周围自由电解质中的 A⁺浓度，而 B^–和 C^–的浓度受到抑制。回到方程（4）中的通量定义，我们看到 B^–和 C^–的低离子浓度对通量有负面影响；即低浓度会导致阻塞。

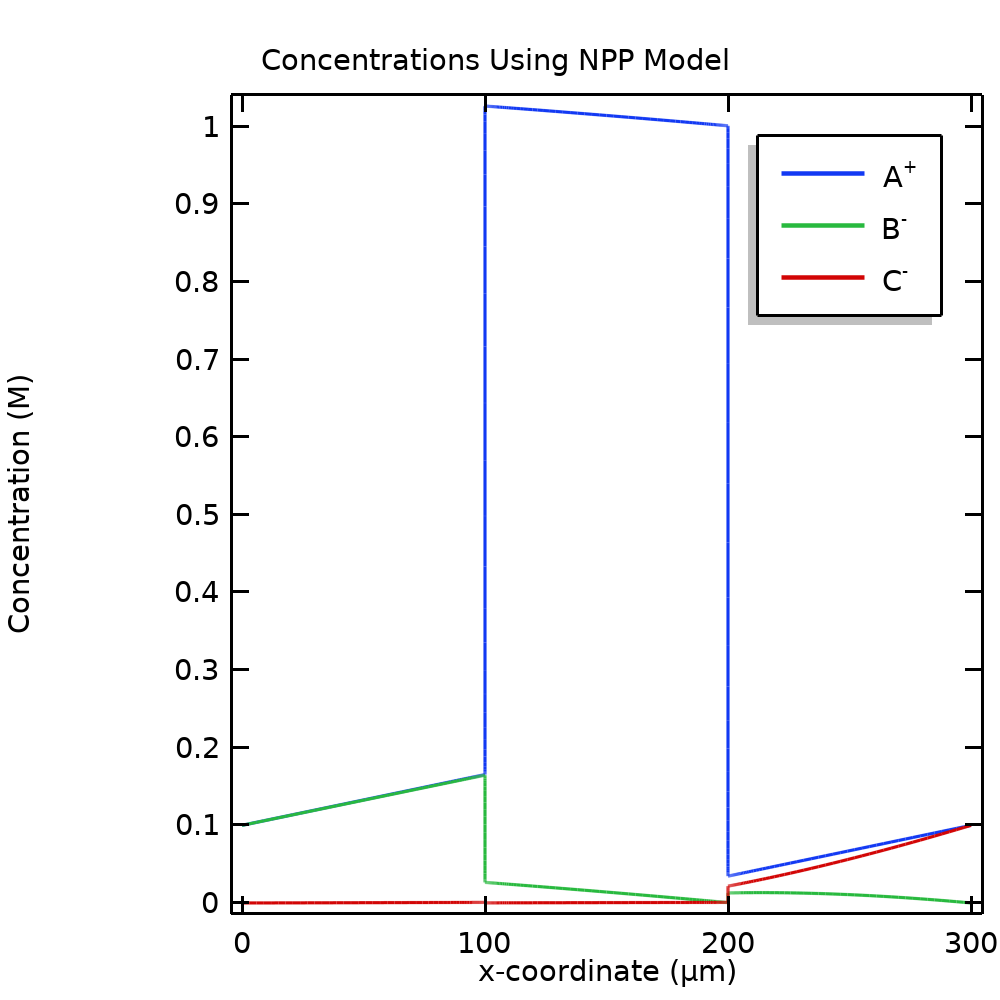
图 4. NPP 模型中移动离子的摩尔浓度。

为什么在自由电解质和离子交换膜之间边界上的梯度非常陡的情况下，膜中的 A⁺增多而 B^–和 C^–却减少了呢？为了找到答案，我们回头看一看方程（1）。观察这个方程，注意，介电常数通常为 10^-12（F/m）量级，我们可以看到，除非非零净电荷被限制在空间中一个非常小的区域，否则偏离零的净空间电荷对电位有着巨大的影响。这样一来，非零空间电荷通常仅存在于靠近相边界的非常窄的区域内，例如电解质-电极界面，或者本例中的膜-自由电解质界面。因此，假设零空间电荷（电中性）对于纳米级相边界以外的任何电解质溶液通常是非常好的近似。由于 A⁺是我们系统中唯一的正离子，加上电中性原因，A⁺的浓度增加到大约与离子交换域中固定负离子的电荷相匹配。

图 5 显示 NPP 模型中的电解质电位图。与图 4 中的浓度变化类似，我们在离子交换和自由电解质域之间的边界上看到了显著的电位变化。由于通过槽的所有物质的通量是恒定的（方程（6）），因此需要电位的大梯度来平衡浓度的大梯度。由于 B^–和 C^–的符号与 A⁺相反，因此 B^–和 C^–的浓度在膜中受到抑制。

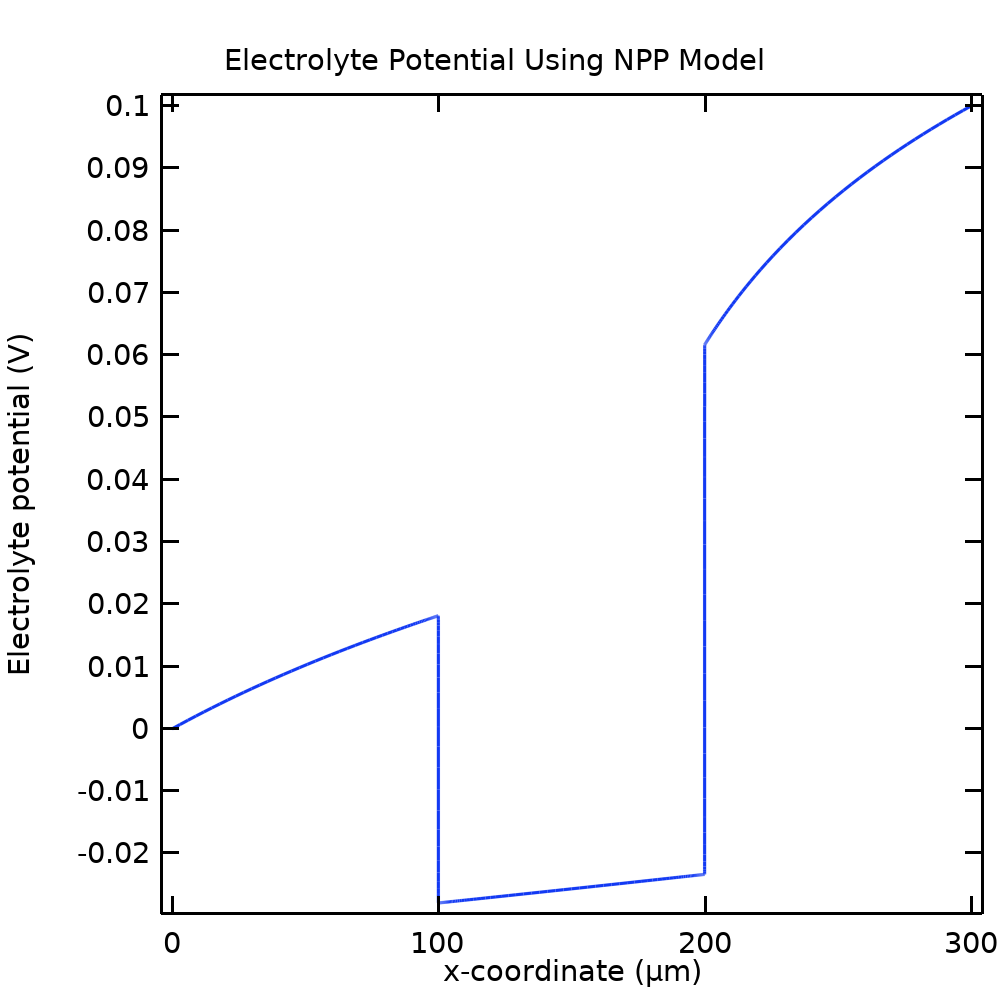
图 5. NPP模型中电解质相的电位。

在图 4 和图 5 中，相边界的浓度和电位梯度都非常高：在绘图中，它们显示为垂直线，由于这些过渡区域中的网格需要很好地解析，因此这会导致数值上的困难。放大图 4 或图 5 会显示过渡区域的厚度约为 1 纳米，因此，通常需要亚纳米级的网格来解析梯度。本例中使用的网格由大约 500 个单元组成。对于一维仿真来说，这通常不是问题。然而，在较高维度下建模时，对精细网格的要求可能会导致内存问题。有没有方法来规避这些过渡区域引起的问题呢？

唐南电位条件和电中性简介

答案是肯定的，我们回到方程（3）中电化学电位的定义。图 6 中绘制的 A⁺的电化学电位（用最左侧边界的浓度作为参考）表明，该电位在整个槽中连续变化，在膜-自由电解质边界没有明显的梯度变化。（绘制 B^–和 C^–的电化学电位也能渲染出相当平滑的曲线）。

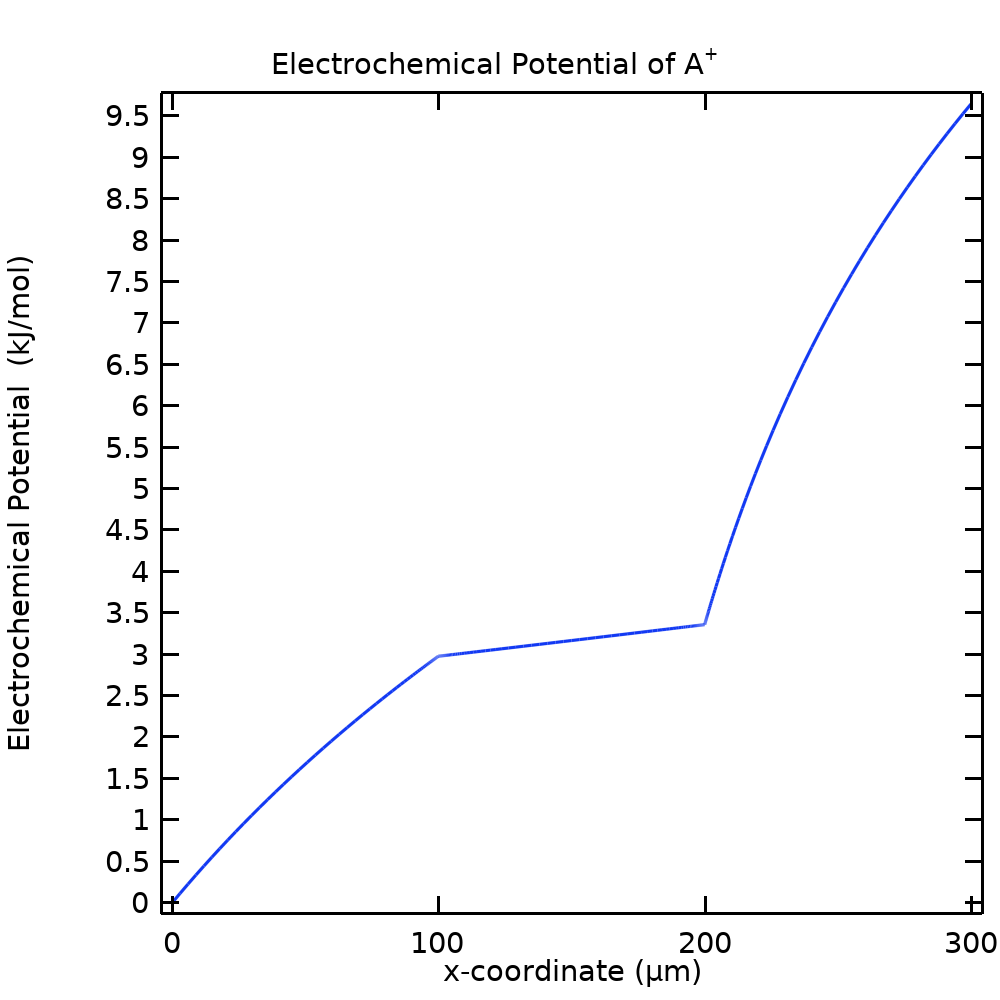
图 6. NPP 模型中 A⁺的电化学电位。

假设过渡区域之外的每一侧的电化学电位相同，这样即可根据下面的公式推导出界面每一侧的离子浓度与电位之间的关系

其中，我们使用任意指数u和d 来定义内部边界每一侧的值。

这种电位变化称为唐南电位。唐南电位为每个移动离子提供了一个本构关系。通过要求离子通量和电中性条件的连续性（通常在相边界纳米级长度范围之外满足），我们可以为所有浓度变量和膜-自由电解质边界上的电位制定一整套内部边界条件。这里需要强调的是，使用这种方案时，我们需要内部边界上的浓度和电位因变量的双重实例，每个实例分别代表从右边或从左边接近边界时的变量值。（这在 COMSOL Multiphysics® 中称为狭缝 条件）。

执行此方案时，我们还可以通过假设所有位置都是电中性来代替域中泊松方程（方程（1））的使用，并基于所有物质通量的总和与它们各自电荷的乘积来推导出一个电位方程

（为方便起见，我们还将总和与 F 相乘，得到一个单位为 A/m²的表达式；即总电流密度。这样，纽曼边界条件可以用这个单位来表示。）

如此一来，浓度变量的数量少了 1个。在这个新的方程组中，我们求解 N-1 个浓度变量和电位变量，记住，我们随时可以根据其他浓度和电中性条件推导出第 N 个浓度。

通过在所有位置使用电中性条件并在内部边界使用唐南电位，可以用少得多的网格单元来求解转化后的模型问题。图 7 绘制了与图 4 相同的浓度，显示了仅使用 15 个网格单元的结果。我们可以看到，除了图 7 中没有梯度突变（图 4 中看起来垂直的线）外，结果看起来是相同的，问题不再需要解析。通过使用唐南电位和电中性假设，我们可以将模型中的自由度数量减少一个数量级以上，而不会降低求解精度。

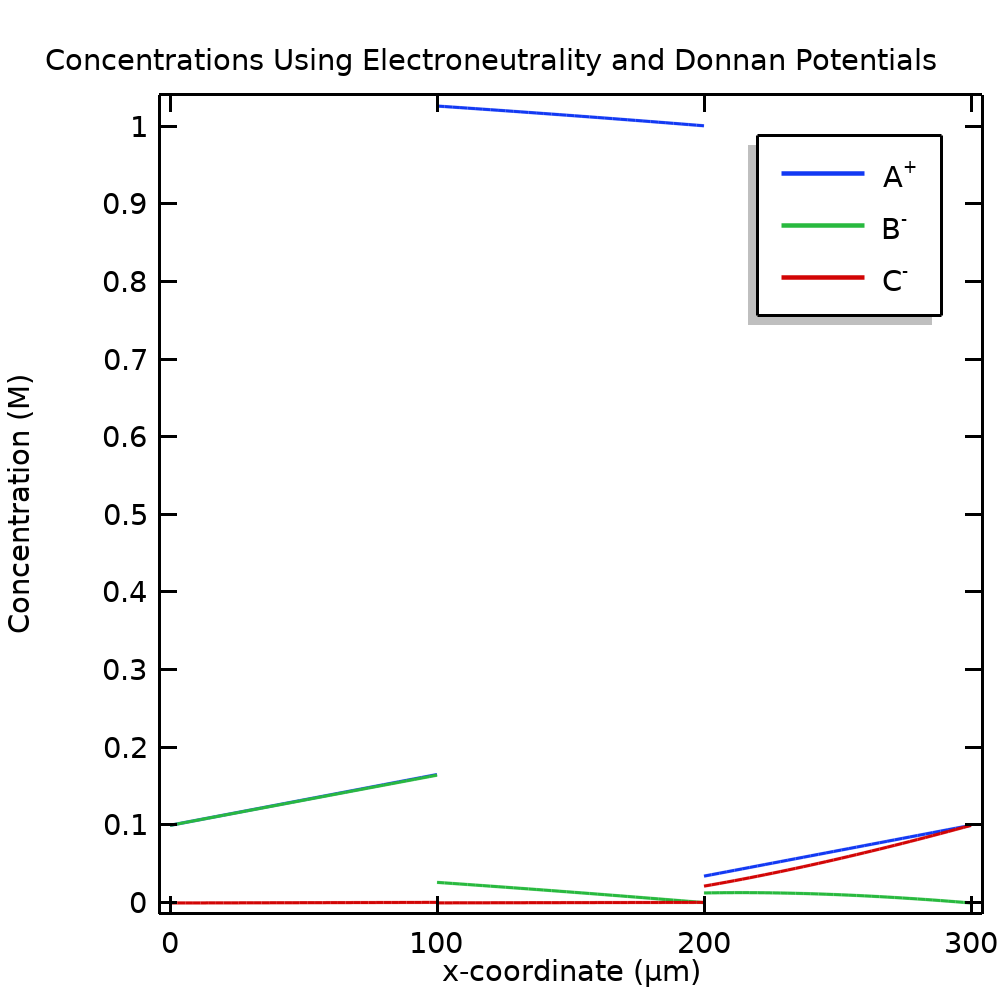
图 7. 使用唐南电位条件和电中性时的浓度。

进一步提高模型收敛性

实际上，模型问题还可以进一步简化：我们可以假设离子交换膜完全阻挡除 A⁺以外的所有离子。在这种情况下，膜中 B^–和 C^–的浓度为 0，由于电中性，A⁺的浓度始终恒定，由固定电荷给出。因此，我们无需求解膜中的任何浓度变量。由于膜中没有 A⁺的浓度梯度，唯一的域方程可以简化为拉普拉斯方程

从中我们注意到，由于电中性，可以得到

恒定电解质电导率可以通过下式计算

尽管此方程是对多个移动离子系统的简化，但应该注意的是，对于单离子导体，如聚合物电解质燃料电池中的 Nafion（其中质子是膜中的唯一移动离子），此方程可以正确进行解析。

拉普拉斯方程特别适合用 COMSOL® 软件在电化学接口中使用的有限元或边界元方法求解。除了进一步降低求解器的自由度和相应的内存需求外，完全阻塞膜这一假设还有助于求解器收敛。例如，不再需要像上文所述的那样，在稳态求解器中使用辅助扫描来提高固定离子浓度。

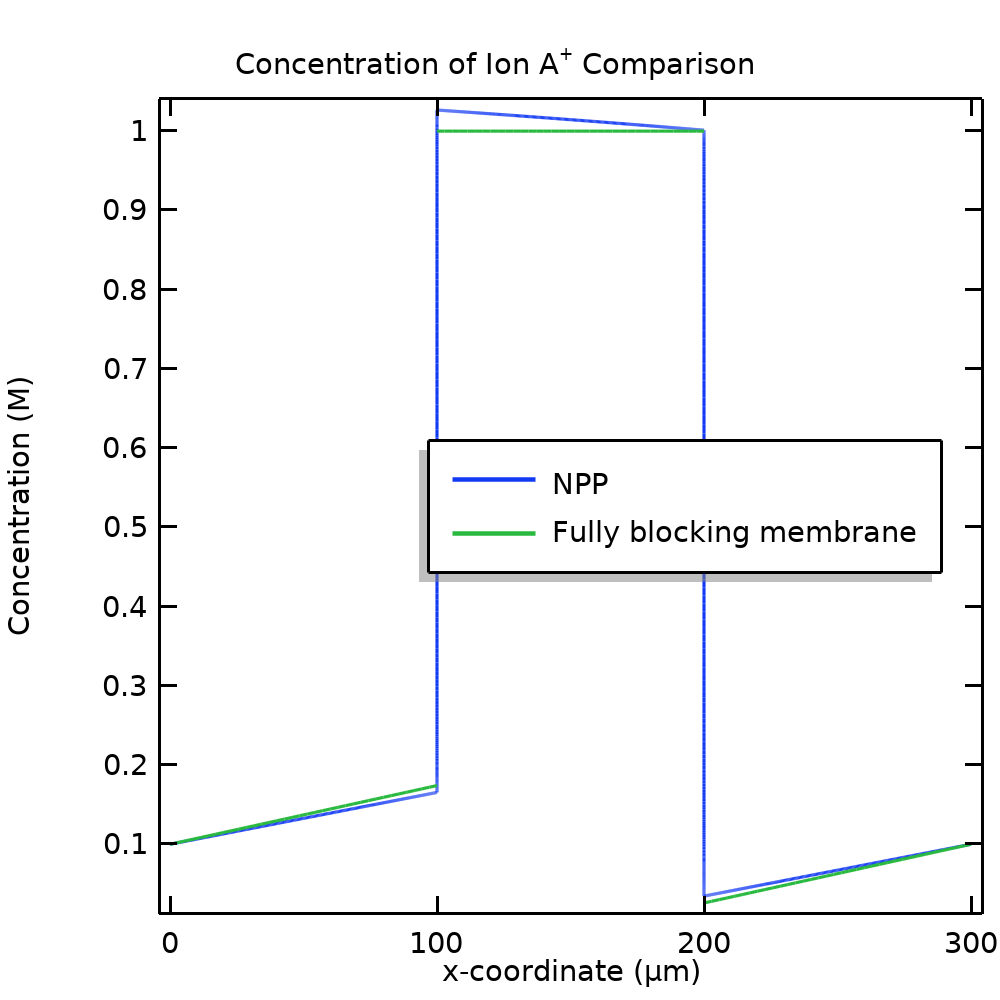
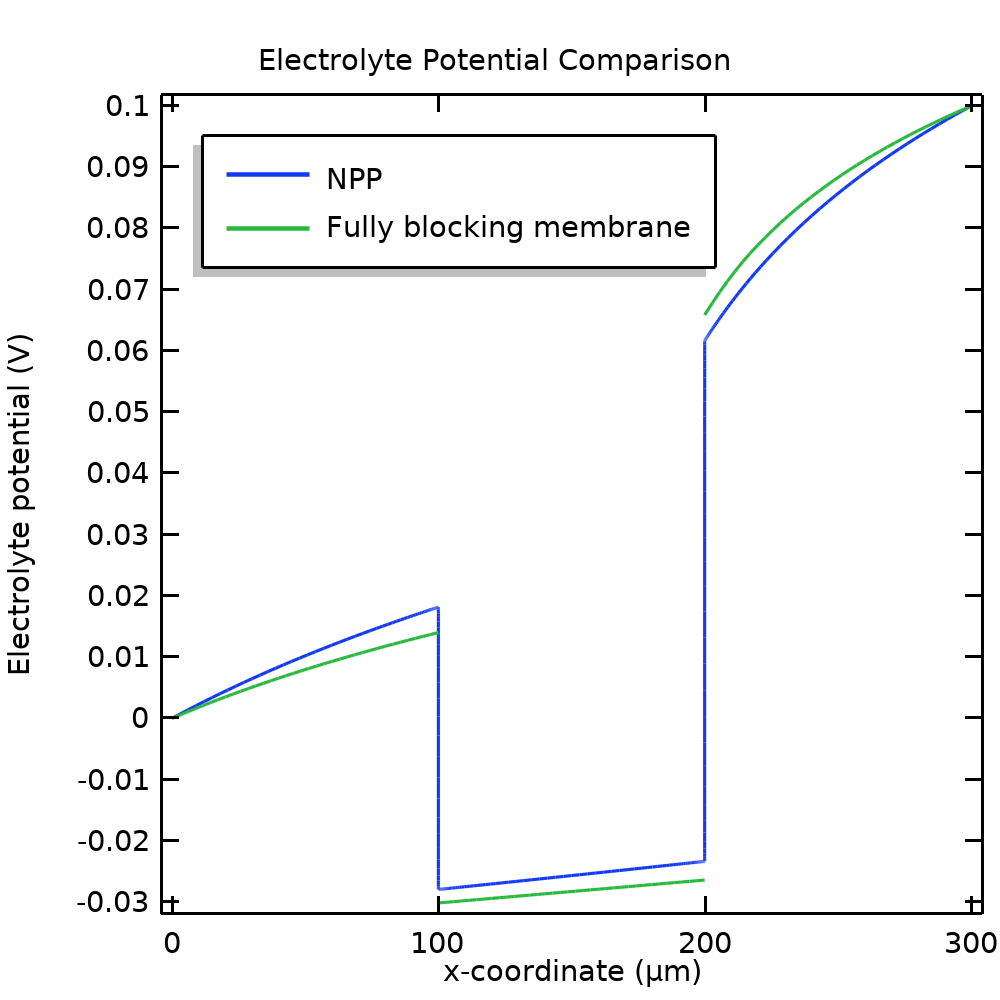
图 8 分别对比了 NPP（使用电中性和唐南条件时的结果相同）模型与使用固定膜电荷的模型的 A⁺浓度和电位。对于我们的示例问题，完全阻塞模型与原始模型相当接近。

图 8. 假设为完全阻塞膜的情况下，NPP 模型与简化模型的 A⁺浓度（左）和电位（右）比较。

如何在 COMSOL Multiphysics® 中为离子交换膜建模

三次电流分布 接口中的离子交换膜 域节点可用于根据电荷守恒模型的选择建立正确的域方程。在电中性情况下，此节点还在邻近电解质域的边界上自动设置唐南条件。还有一个离子交换膜 边界节点，可用于在不同的物理场接口之间的边界上设置唐南条件。

为了建立 NPP 模型，我们可以使用三次电流分布 接口的一个实例，其中电荷守恒模型设为泊松。然后我们可以用电解质 域来定义自由电解质域，用离子交换膜 节点来定义膜域。

为了基于电中性和唐南条件建立模型，我们可以按照上述内容继续操作，但是需要将电荷守恒模型切换为电中性，此操作会自动将唐南条件应用到内部边界。

建立完全阻塞膜模型需要更多的步骤。由于单独的浓度变量是在膜的每一侧进行求解（左边是 A+ 和 B-；右边是 A+ 和 C-），我们必须使用三次电流分布 接口的两个独立实例（电荷守恒模型设为电中性 ）。我们可以使用膜的二次电流分布 接口，通过拉普拉斯方程和三次电流分布 接口中的离子交换膜边界 节点来求解电位，从而设置唐南电位条件。

后续操作

如果你有 COMSOL Access 帐户和有效的软件许可证，便可从“案例下载”页面下载该模型的 MPH 文件。

如需了解有关电化学应用建模的更多信息，请阅读本篇博客文章：通过建模改进钒氧化还原液流电池。

编者按：本篇博客文章于 2018 年 10 月 25 日更新，现在包含 COMSOL Multiphysics 5.4 版本新增特征的信息。

Nafion 是 The Chemours Company FC, LLC. 的注册商标。