
模拟等离子体时,有多种离子温度选项可供您选择。但您的选择可能会强烈影响模型的结果。我们将讨论现象背后的理论原因,并通过研究感应耦合等离子体 (ICP)示例来展示不同离子温度选项对模型结果的影响。
离子温度的选择
非平衡冷等离子体的一大特征是电子温度远高于气体温度。模拟等离子体时,离子温度通常设为等于气体温度。这是一个可以接受的近似,只要离子会与中性气体分子发生足够多的碰撞,之后就将与背景气体一起被加热。感应耦合等离子体 (ICP) 中的情况尤其如此,反应器中的压力低,离子的平均自由程长度接近等离子体反应器的长度尺度。除此之外,如果碰撞次数较少,那么离子温度将介于气体与电子温度之间。
虽然 COMSOL Multiphysics 并没有求解离子温度,但为您提供了一些相关选项。
您可以选择将离子温度设为等于气体温度或者用户定义的值或表达式。此外,我们还建议您通过 COMSOL 软件提供的局部场近似 (LFA) 定义电场与离子迁移率之间的相关性,并使用 Einstein 关系式计算。
如前所述,您对离子温度的选择(特别是对低压等离子体)会显著影响您的模型结果。您可以在下节找到这一现象的理论解释。
理论背景
对于重物质传递(及离子传递)而言,会针对每类物质求解含漂移扩散近似的连续性方程。k 物质质量分数的变化 w_k 依赖于通量 \mathbf{j}_k 和反应项 R_k。简单起见,本例中忽略了对流及热扩散项:
为了计算通量 \mathbf j_k,我们需要知道混合物的平均扩散系数 D_{k,m} 和离子迁移率 \mu_{k,m}:
基于气体动力学理论计算了二元扩散系数 D_{kj},以便得到混合物的平均扩散系数 D_{k,m}。您可能已经注意到,需要单独为每类等离子体指定 Lenard-Jones 参数 \sigma 和 \epsilon / k_B:
根据 Einstein 关系式计算离子迁移率:
在反应器壁处,按照以下公式计算了壁面的离子通量 \mathbf j_k:
需要离子温度计算反应器壁面的通量和离子迁移率,因此对离子温度的选择尤其会影响等离子体模型内的离子传递属性。如果通量中的迁移部分要大于扩散部分,那离子温度选择的重要性将更为明显。这一点尤其适用于极低压力或较高电场强度的情况。
局部场近似 (LFA) 的使用
重申一次,您还可以借助 COMSOL Multiphysics 的 LFA 特征计算离子温度。
LFA 假定粒子的局部速度分布与局部电场平衡。因此,类似离子温度或离子迁移率等的物理量可以表示为(约化)电场中的项。LFA 要求电场的局部变化相比平均自由程的长度要小。但这并非全对,特别是在边界层中。
对于下述作为约化场函数的约化电子迁移率表达式,我们将在接下来的 ICP 示例中用到这一表达式。
在上述方程中,约化电场 E/n 的单位是 Townsends (Td) 。
感应耦合等离子体示例
为了表示离子温度选择对 ICP 模型的影响,我们将分析一个示例。
我们使用不同的离子温度对感应耦合等离子体反应器进行了三次模拟,模型类似于 GEC ICP 反应器,氩化学模型。因为 ICP 会在极低的压力下工作,所以需要仔细考虑离子温度的选择。
离子温度为:
- 模型 1:设为 300 K,对应于气体温度。
- 模型 2:设为 0.1 eV (1160 K),对应于典型的文献值。
- 模型 3:设为 D_{k,m} / \mu_{k,m},使用 LFA 计算得到 \mu_{k,m}。
其他模型参数如下:
| 模型参数 | |
|---|---|
| 气体温度 | 300 K |
| 线圈功率 | 500 W |
| 压力 | 0.02 torr |
| 电子迁移率 | 4E24 (1/(m*V*s)) |
模型 3 中的平均离子温度通过 D_{k,m} / \mu_{k,m} 计算,为 0.22 eV –(或 2515 K)。
下图表征了经 0.001 s 后三个模型中的电子密度。
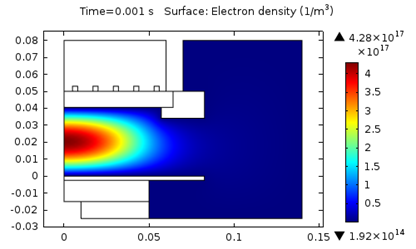
模型 1:电子密度 (T_ion = 300 K)。
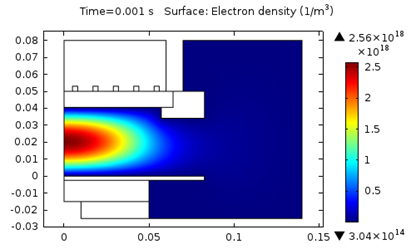
模型 2:电子密度 (T_ion = 0.1 eV)。
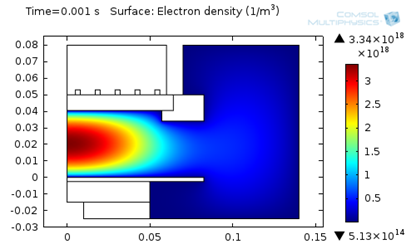
模型 3:电子密度 (使用 LFA 计算得到 T_ion)。
如上所示,使用更高的离子温度会显著提高电子密度。
我们在下表中对比了模拟结果,并给出了最大电子密度、最高电子温度和吸收功率。
| 最大电子密度 [1/m³] | 最高电子温度 [eV] | 电阻损耗 [W] | |
|---|---|---|---|
| 1. T_i = 300 \text K | 4.3E17 | 4.1 | 387 |
| 2. T_i = 0.1 \text {eV} | 2.6E18 | 2.8 | 407 |
| 3. 局部场近似 | 3.3E18 | 2.3 | 41 |
从上表中得出,离子温度的升高会造成电子密度和吸收功率的显著上升。此外,电子温度则会明显下降。
上例显示了离子温度选择对 ICP 模拟结果的影响。最后将结果与文献值进行对比,这对于确定可以通过哪个假设得出最好的结果至关重要。






评论 (7)
刘 阳
2016-02-26博主您好,请问相关的模型可以分享一下么?
彦鹏 王
2017-11-18多谢博主,一直没搞清楚怎么优化离子效应带来的影响,如醍醐灌顶!
宇航 秦
2017-11-20王彦鹏,您好!
非常感谢您的帮助。
秦宇航
宇航 秦
2017-11-20王彦鹏,您好!
非常感谢您的关注。
秦宇航
亚萌 薛
2018-01-04我想问下 约化场是什么意思
peiqi chen
2018-10-12我想问一下模型结果为什么没有看到等离子体鞘层呢?
王 刚
2018-10-19约化场是将变量除以某个参考值之后的场变量分布。模型中的等离子体鞘层可以通过放大局部来观察。