
本篇博客中,我们介绍了线性静态有限元问题的网格剖分注意事项。这是网格剖分技巧系列博客的第一篇,希望能帮您建立起对有限元模型剖分网格的信心。
关于有限元网格剖分
有限元网格通常服务于两大目的。首先,它将模拟的 CAD 几何细分为更小的组成部分,或称单元,在此基础上,我们将能够写出一组方程来描述控制方程的解。网格也用于代表所求解物理场的解域。不论是几何离散化还是解的离散化,都会出现误差,所以我们将分别查看。
几何离散化
考虑两个非常简单的几何,一个立方体和一个柱形壳:

我们可以使用四类单元来剖分这些几何 – 四面体、六面体、三角棱柱,以及金字塔形单元:
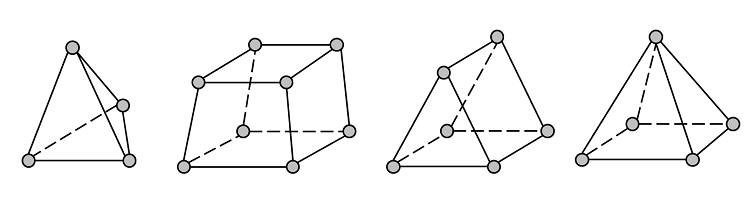
灰圈代表单元的角,或称节点。您可以使用这四种单元的任意组合。(在二维模型中,可以使用三角形和四边形单元。)检查一下您将发现,这两个几何都可以通过一个六面体单元、两个棱柱、三个金字塔形,或五个四面体进行网格剖分。正如我们在之前一篇有关求解线性静态有限元问题博客中读到的,您总可以通过一次 Newton-Raphson 迭代得到解。在所有线性有限元问题中,不论您使用了哪种网格,这一点都适用。让我们看一下可以在这些结构中使用的最简单网格。下图显示了用于离散这些几何的单个六面体单元:
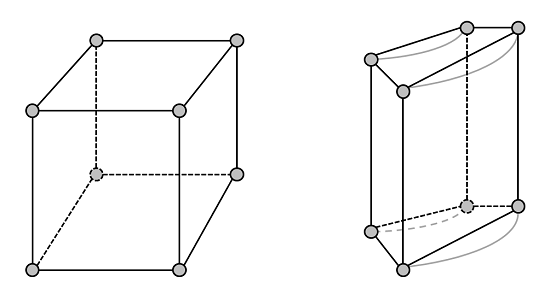
立方体的网格显然是真实几何的完美表征,柱形壳的网格则看起来相当差。事实上,这只是因为绘制的关系才看起来如此。出于图形表现的目的,绘制在屏幕上的单元通常会有直的边,但 COMSOL 则会使用二阶拉格朗日单元来离散几何(以及解)。因此,虽然单元的边看上去是直的,它的内部表征其实是:
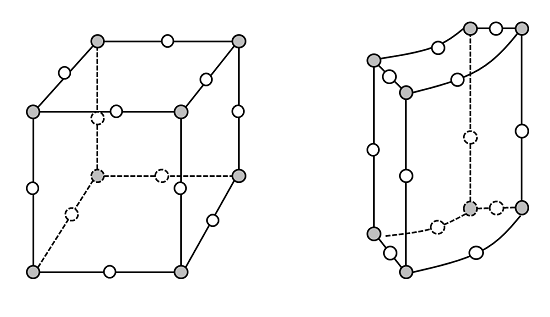
白圈代表这些二阶单元边的中点节点。也就是说,定义了单元边的线由三个点表征,这些边通过多项式拟合近似。每个四边形面的中心,以及二阶拉格朗日六面体单元(为清晰起见,图中已省略)的中心也有一些额外的节点。显然,这些单元在代表单元中弯曲边界方面的表现更好。缺省情况下,COMSOL 会在大部分物理场中使用二阶单元,化学物质传递问题和流体流动场中的求解是两个例外。(由于这类问题中以对流为主,使用一阶单元求解控制方程会更好。)还可以使用更高阶单元,但缺省的二阶单元通常能在精度和计算要求之间达到一个较好的折中。
下图显示了当使用一阶和二阶单元剖分一个 90° 弧时的几何离散化误差:
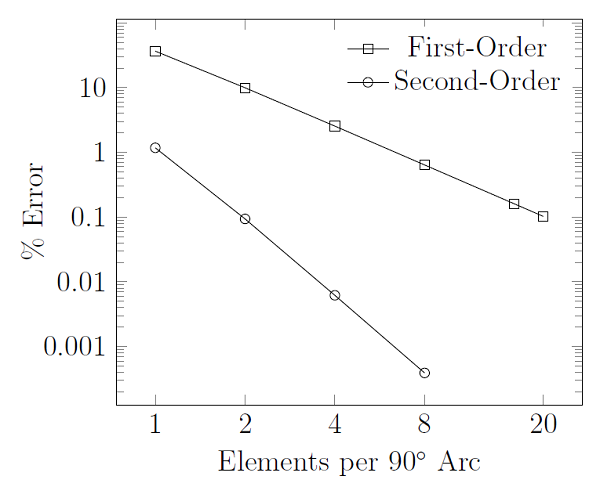
据此我们可以得出以下结论:至少需要 2 个二阶单元或 8 个一阶单元才能将几何离散化误差降低到 1% 以下。事实上,使用 2 个二阶单元会引入小于 0.1% 的几何离散化误差。更细化的网格可以更精确地表示几何,但将使用更多的计算资源。这也给了我们两条相当实用的指导:
- 使用一阶单元时,调整网格以保证每个 90° 弧中至少包含 8 个单元
- 使用二阶单元时,每个 90° 弧中至少使用 2 个单元
根据这些经验法则,我们现在可以估算在对几何进行网格剖分时引入的误差,这样即使还没开始求解模型,也能对剖分操作有一定信心。现在,让我们将注意力转向网格如何离散解这一点上。
解的离散化
有限元网格也用于表示解的域。在解节点处计算,并基于多项式在整个单元上内插该解,以得到整个解的域。当求解线性有限元问题时,不论网格有多粗化,我们总能够计算得到解,虽然可能并不精确。要理解网格密度对解精度的影响,让我们看一下之前几何中的一个简单传热问题:
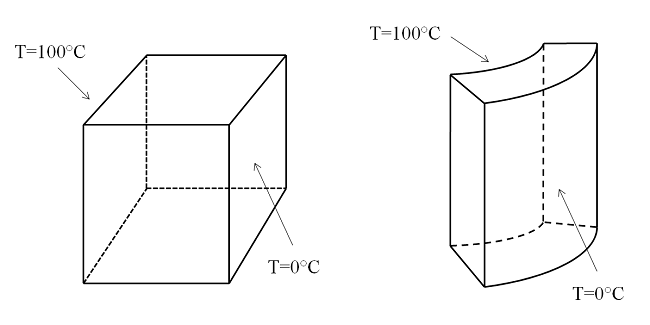
在立方体和柱形壳相对的面上施加了一个温差。导热系数恒定,所有其他表面均为热绝缘。
立方体的解是温度场在整个立方体中呈线性变化。对本模型而言,一个一阶六面体单元已足以得到真实的解。当然,您很少会这么幸运!
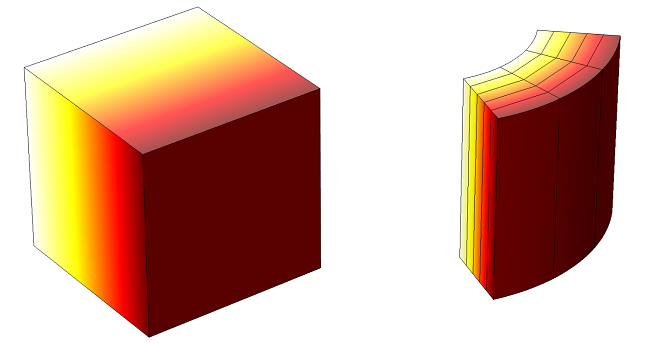
因此,让我们看一个略具挑战性的案例。我们已经看到,柱形壳模型因弯曲边的存在而包含几何离散化误差,因此我们将沿弯曲边使用 2 个二阶(或 8 个一阶)单元开始模型研究。如果仔细看一下上图,您将发现边界上单元的边是弯曲的,而内部单元的边则是直的。
沿柱体的轴向,我们可以只使用一个单元,因为温度场在此方向无变化。但从内表面到外表面的径向上,我们还需要足够的单元来离散化解。本案例中的解析解为 \ln(r),可与我们的有限元解进行对比。由于多项式基函数无法完美描述该函数,让我们绘制一下线性和二阶单元有限元解的误差:
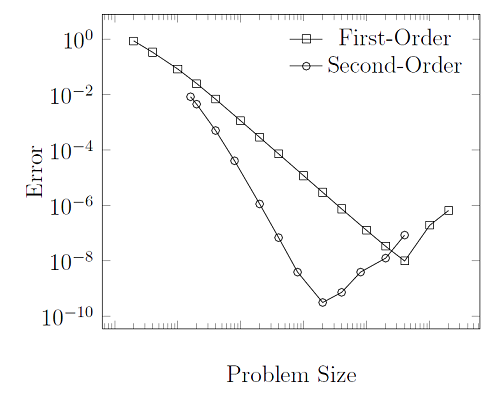
从这一绘图中可以看到,误差将随着您增加模型中的单元数目而减小。这也是有限元方法的一个基本特点:单元越多,您的解越精确。当然,这样做也要付出一定的代价:我们需要更多的计算资源、时间和硬件来求解更大型的模型。现在,您已经注意到绘图的 x 轴没有单位,这是我们的特意设定。每个模型中误差相对于网格细化的减小速率不同,这与许多因素相关。唯一重要的一点是,它在适定的问题中会不断呈单调式下降。
您还将发现,在某个点后,误差会重新升高。这将在单个网格单元变得非常小的时候发生,我们碰到了数值精度的限制。也就是说,我们模型中的数小于电脑可以精确表示的数。这是所有计算方法中固有的一个问题,而非仅存在于有限元方法中;计算机无法精确表示所有实数。误差开始重新增大的那个点接近 \sqrt{2^{-52}} \approx 1.5 \times 10^{-8},出于安全和实用的考虑,我们经常说最小可实现的误差是 10-6。因此,如果我们积分整个模型中真实和计算解的缩放差:
我们就可以说在网格细化的限制下,误差 \epsilon 通常可以小至 10-6。实际上,模型输入的不确定性通常比它更大。同时也请记住,我们通常并不知道真实的解,相反,我们需要对比由不同尺寸网格计算得到的解,并观察解正朝哪个值收敛。
自适应网格细化
我希望通过介绍一个更好的网格细化方法来结束本篇博客。上图显示出,随着模型中所有单元变小,误差会减少。但理想情况下,您仅需细化误差较高区域的单元。COMSOL 通过自适应网格细化解决了该问题,它首先会在初始网格上求解,然后在误差估算较高的区域迭代插入单元,然后重新求解模型。您可以按照需要进行足够多的迭代。本功能可用于二维下的三角形单元和三维下的四面体单元。让我们在一个简单的结构力学问题中检查一下该问题,单轴拉伸下的有孔平板,如下图所示。利用对称性,我们仅需求解模型的 1/4。
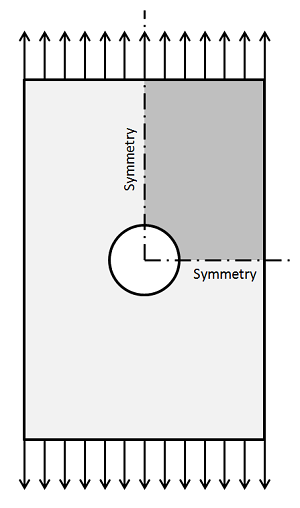
在离孔洞较远的地方,计算得到的位移场和合应力都比较均匀,但靠近孔洞处的变化很大。下图显示了初始网格,及几次自适应网格细化迭代后的结果,以及计算得到的应力场。
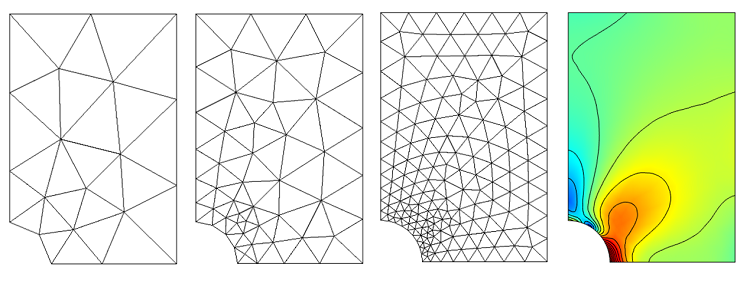
请注意 COMSOL 如何优先在孔洞周围插入更小的单元。这应该不奇怪,因为我们已经知道孔洞周围的应力更高。实际上,我们建议综合自适应网格细化、工程判断,以及个人经验来找到一个可接受的网格。
要点总结
- 您总应执行网格细化研究,并对比不同尺寸网格的结果
- 利用您有关几何离散化误差的知识,起始网格尽量粗化,然后再细化
- 您可以使用自适应网格细化,或您自己的工程判断来细化网格





评论 (0)