
COMSOL Multiphysics 包含两个可用于手动定义有限元网格变形的接口,变形几何 接口和移动网格 接口。本篇博客中,我们将介绍应何时使用这些接口,以及如何通过它们来高效模拟平移运动。
使用变形网格的优势
假设我们希望通过 COMSOL Multiphysics 模型来描述一个在较大域内移动的固体对象,域内充满诸如空气等的流体,甚至可以是真空环境。首先假定对象随时间的移动路径已知,我们不必担心需要使用哪个物理场求解模型,但将假定希望求解移动域及周围域中的一些场。当然,我们还需要在这两个区域使用有限元网格,但网格将发生改变。
在较大域中沿已知路径自由移动的固体对象。
针对这种情景,我们有两个选项:变形几何 接口和移动网格 接口。这两个接口的作用完全相同,但适合不同的情况。
- 当我们希望明确定义材料在域中每点处的应变时,应使用移动网格 接口。它特别适用于模拟固体域的形变可以完全确定的情况。体积的变化说明材料被拉伸或压缩,但总质量保持不变。
- 当只需定义域边界处的形状时,可以使用变形几何 接口。它最适合模拟流体域。域总体积的变化说明了模型质量的增加或减少。
这两个接口的实际使用完全相同,但对每类物理场的处理不同,所以您应根据求解的物理场进行选择。虽然我们不会在本篇博客中介绍如何在这两个接口中进行选择,但您可以从阅读 COMSOL Multiphysics Reference Manual 中的“变形网格基础”和“处理传热中的框架”章节开始。
另外请注意,我们无法耦合固体力学 接口与移动网格 接口。固体力学 接口主要通过动量守恒计算域的变形。其他物理场,比如固体传热,则支持在这一变形中求解。另一方面,如果您希望研究由于移除材料造成的应力变化,或希望能在不对整个几何进行参数化的同时对某个维度进行参数化扫描,如“对导入 CAD 文件中的维度执行参数化”博客中的介绍,结合变形几何 接口与固体力学 接口会是较合理的做法。
我们将在这里介绍网格移动的基本概念,分析一个固体对象在稳态边界包围的较大域内的移动,如上图所示。对象随时间的运动轨迹已知。我们将分析如何针对这一问题设定变形几何接口。但我们首先需要快速查看 COMSOL Multiphysics 中将求解的方程组。
正在求解哪些方程组?
对象在域内的运动问题其实是一个边界值问题。所有边界的位移已知,并能用于定义网格在两个域内的变形。
针对网格在每个域内的变形,我们有四种计算方法:Laplace、Winslow、超弹性和 Yeoh 平滑类型。这里,我们将仅分析最简单的情况——Laplace平滑,并将说明为何这种方法能解决大部分问题。Laplace 平滑方法在域内求解了以下偏微分方程:
其中,小写的 x、y 及 z 是网格的变形位置,大写的 (X,Y,Z) 指未变形前的初始位置。
由于所有边界的位移已知,所以这是一个适定问题,而且从理论上讲,方程的解将给出网格的变形。但在实际操作中,我们会碰到一些计算得到的变形场并没有多大用处的情况。如下图所示,其中显示了原始域中的原始网格,以及当固体沿对角线运动时的变形网格。请仔细观察我们突出显示的区域,您将发现移动固体边处的网格发生了严重变形,特别是在尖角处。变形超过某个程度后,严重变形会使模型无法再求解上述方程。
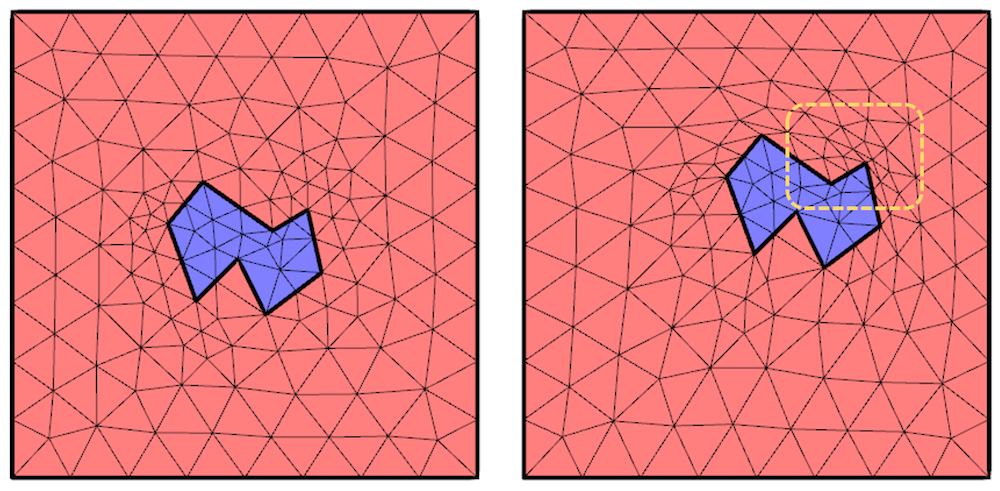
原始及变形网格,突出了网格变得严重扭曲的区域。
在上图中,可以通过边界完整描述及指定蓝色域内的变形。另一方面,红色域内的变形则需要求解上述偏微分方程,这会造成一些困难。我们所需要的是一种能模拟更大的变形、但同时能最小化网格变形的方法。
如何帮助网格变形?
如果您有相关数学背景,就会发现上述控制方程实际就是 Laplace 方程,您甚至还可能知道它在一些简单情况下的解。其中较简单的一个情况是,Laplace 方程在包含狄氏边界条件的笛卡尔坐标域中的解与每条边界呈高度线性,且沿周长连续。在此例中,域内的解等于四个角处边界条件间的双线性内插。事实证明,您可以使用双线性内插求出含直边的所有凸四边形域中 Laplace 方程的解。
我们首先要将复杂的变形域细分为多个含直边的凸四边形域。下图显示了其中一种可能的细分方法。

对域进行细分,变形区域(红色)将由凸四边形域构成。
变形域被分为多个凸四边形域。事实上,我们也可以将它分为三角形域,因为这是一类特殊的四边形,两个端点的位置重合,也就是所谓的退化域。如果无法将域分为四边形,将只需将其分为多个三角形。
既然我们引入了新的边界,就需要完整定义所有边界,以便分析域内的变形。变形域的相邻边界已知,且边界外不存在变形。但与这些边界相连的部分呢?我们画了一条直线来连接两个变形已知的点,因此可以直接沿这些线应用线性内插来指定此处的变形。
如何轻松计算这一线性内插呢?也许您已经猜到,我们只需简单求解这些连线处的 Laplace 方程!
常见做法是在模型中增加系数型边界偏微分方程接口,求解两个用于描述这四条边界中每条位移的变量。该接口支持您指定偏微分方程的系数,以便沿一条边界设定 Laplace 方程。边界任一端点处的位移已知,因此我们就有了一个针对沿边界位移的边界值问题,该问题经完整定义并支持求解。
新的助应变量完整定义了变形域。结果如下方所示,并表明能够支持更大的网格变形。当然,我们在移动对象时应避免它与边界发生碰撞,因为这将造成域拓扑的变化;同样,单元面积不能为零。但我们可以将变形域设得极为细小。
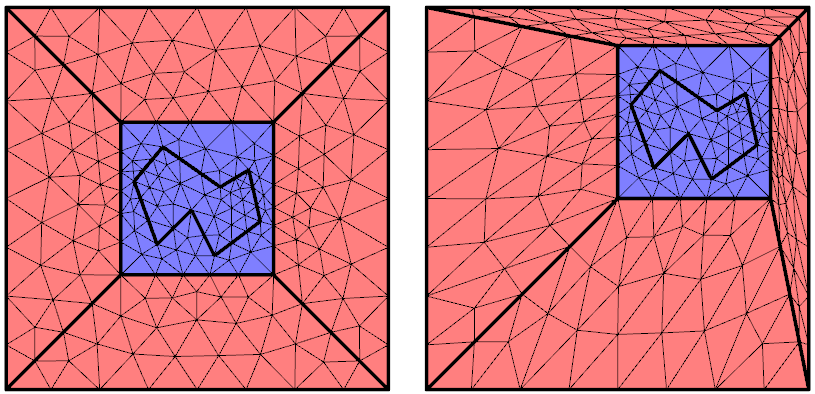
变形几何中沿内部边界增加助应变量后,未变形和变形网格。
您可能认为上方网格中的变形程度已经很高,但请记住所有变形单元仍包含直边,这一点非常好。在实际中,您经常会发现即使在高度变形的单元中也能得到良好的结果。
但我们可以观察到,移动域内的某个区域会包含一些发生了高度变形的极小网格,另一个区域则会包含经拉伸的较大网格。因此最后一步是使用自动重新剖分网格,它会根据网格的质量度量停止瞬态仿真,然后针对当前变形重新进行网格剖分。
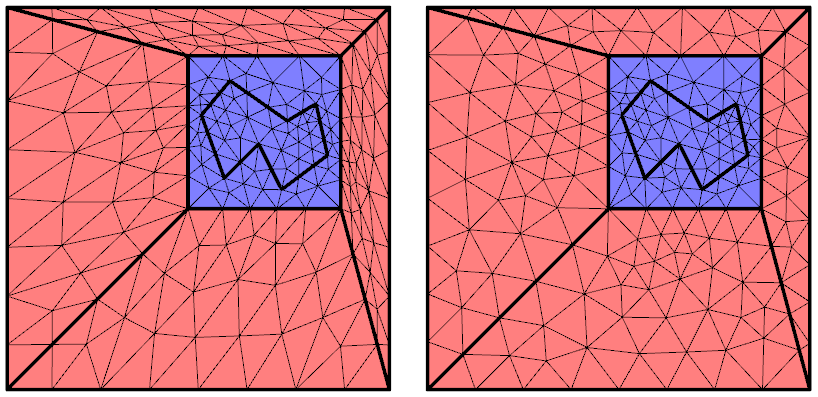
执行自动重新剖分网格前后的变形几何。
从上图中可以看到,自动重新剖分网格会在挤压区域生成较少的单元,并增加拉伸区域的单元数,从而保持单元分布均匀。网格中总的单元数基本保持不变。但重新剖分会增加计算负担,因此我们只应在单元变形会严重影响结果的精度时使用这一特征。
如果存在未知变形呢?
之前的分析适用于固体对象在流体域中的移动已知的情况。但如果固体中存在未知变形呢?比如施加了在求解时计算得到的某些载荷?流固耦合分析就是这样一个经典示例,其中固体会在周围流体流动的影响下发生变形。
针对这一情况,我们可以使用积分组件耦合算子,它支持在整个模型空间使用变形固体结构中某一点处的变形;随即可以使用一个或更多点的变形来控制网格的变形。微泵机理教程模型较好地展示了这一技巧的使用。下图是对此技巧的图形化显示。
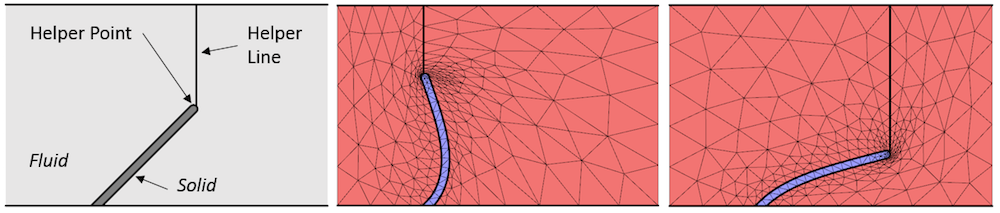
当实际变形未知时,针对某个点的积分组件耦合可用于定义控制网格变形的辅助线。
从上图中可以观察到,模拟域并没有被分为凸四边形,且辅助线可以沿模拟域的上边界滑动。因此这种模拟方法并没有那么严格,但仍允许网格发生较大变形。很显然,所有情况并非都只有唯一的最优解决方案。您可以在具体案例中尝试结合几种技巧。
小结
我们介绍了如何有效使用变形网格接口,这可以通过将变形域分解为四边形域并沿边界引入助因变量实现。这种方法简化了 COMSOL Multiphysics 软件对该类问题的求解。当存在严重变形时,可以通过自动重新剖分网格来帮助求解博客介绍的方法同样可以用于三维几何。模拟变形网格教程使用二维示例演示了这一方法。
至此,我们仅讨论了对象在相对简单域内的平移,我们可以轻松在其中设定变形域。当很难对几何进行细分或对象会发生旋转时,我们将需要不同的方法。在接下来的系列博客中,我们将介绍这一主题,敬请期待。
编者注:本篇博客于 2018 年 6 月 25 日更新,修改了有关 Laplace 平滑方法的一节内容。



评论 (11)
小强 张
2017-08-17楼主 可以分享一下你这个模型吗?zxq92826@163.com
could you share your model? thank you E-mail: zxq92826@163.com
宇航 秦
2017-08-17张小强,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
欣峰 张
2017-09-11固体力学接口的线性变形真的不能和移动网格接口耦合吗?我的comsol仿真出现的问题是将固体力学和移动网格耦合在一起时,变形后会出现一部分空白的部分,这一点很不理解,能帮忙讲解一下吗?
宇航 秦
2017-09-11张欣峰,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
壮 雍
2019-01-04某人 王
2020-07-03请问三维模型中,如何创建边界?通过线段或者多边形连接大小正方体顶点无法成为边界被选择。
Haili Wang
2020-07-15 COMSOL 员工王某人,您好!
感谢您的评论。
若要在三维几何中形成一个平面的话,可以采用新建工作平面,然后利用该工作平面对原始进行“分割”。这样就能得到相应的工作平面。
祝好!
定鼎 吴
2021-11-12请问三维示例在哪?在“模拟变形网格”教程中并没有找到。
Qihang Lin
2021-11-24 COMSOL 员工您好,该案例确实不包含三维示例,但三维中的设计思路核心与二维模型非常类似。您可以在吸收这篇博客知识后查看其他的三维动网格示例进行学习:http://cn.comsol.com/model/electrodynamics-of-a-power-switch-33511
Wenfeng Wu
2023-12-27你好,请问内部的小正方有可能运动到跟外部大正方形边界重合的位置吗,网格是否可以被挤压消失
Haoze Wang
2023-12-28 COMSOL 员工您好,网格不可以消失。