
本篇博客中,我们将向您介绍使用 COMSOL 求解任何有限元问题时,其中所用的两类线性方程组的求解算法。这些信息与理解求解器的内部工作原理,以及内存使用如何随问题大小变化等相关。
线性静态有限元问题
让我们考虑一个包含三个节点和三个单元的线性静态有限元问题:
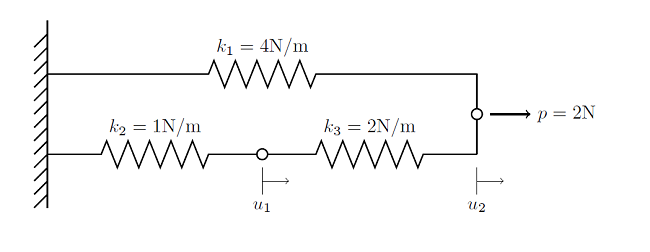
每个单元由两个节点约束。其中一个节点位于刚性壁处,我们知道这里的位移是 0,因此无需求解该节点。正如我们在之前一篇有关求解线性静态有限元问题的博客中读到的,我们可以为每个节点编写出一个力的平衡方程:
而且,我们可以这样写:
或者更加简洁的形式:
我们可以使用 Newton-Raphson 迭代方法来求解此问题,由于这是一个线性静态问题,我们可以通过一次迭代求解,并使用 \mathbf{u}_{init}=\mathbf{0} 作为初始值,此时将得到如下解:
现在,该问题仅包含两个未知项,或称自由度 (DOF),可以轻松通过笔算求解。但整体而言,您的矩阵通常会包含数千乃至数百万个 DOF,对上述方程的求解通常是整个问题中计算量最大的部分。当在计算机中求解此类线性方程组时,我们还应了解条件数的概念,这是一种测量解对载荷变化敏感性的方法。虽然 COMSOL 不会直接计算条件数(这样做的成本与求解问题相同),我们还是会提供条件数的相关项目。在用于求解线性方程组的数值方法中,我们就需要条件数。
我们有两个用于求解 \bf{K^{-1}b} 的基础类算法:直接和迭代方法。下面,我们将简要介绍这两类方法,它们的一般属性,以及相对表现。
直接方法
COMSOL 中使用的直接求解器是 MUMPS、PARDISO,以及 SPOOLES 求解器。所有求解器都基于 LU 分解。
对于所有良态有限元问题,这些求解器都能得到相同的答案,这就是它们最大的优势;它们甚至支持求解一些非常病态的问题。从解的角度来看,您选择哪个直接求解器并不重要,因为它们都将返回相同的解。不同直接求解器之间的主要区别在于其相对速度。MUMPS、PARDISO 和 SPOOLES 求解器每个都可以利用单台机器上的所有处理器内核,但 PARDISO 最快,SPOOLES 最慢。在所有直接求解器中,SPOOLES 使用的内存最少。所有直接求解器都需要使用大量的 RAM,但 MUMPS 和 PARDISO 可以在核外储存解,这意味着它们能够将部分问题卸载到硬盘上。MUMPS 求解器也支持集群计算,使您可用的内存大于通常任一台机器中所能提供的。
如果您在求解一个没有解的问题,例如没有约束却有载荷的结构力学问题,直接求解器仍会尝试求解,但会返回一个与下方所示类似的错误信息:
求解失败。 相对残差(0.06)大于相对容差。 返回的结果未收敛。
如果收到此类报错,您应检查问题是否被正确约束。
迭代方法
COMSOL 中包含大量的迭代求解器,但它们在本质上与共轭梯度法类似,所以概念相当简单,不难理解其最高级形式。其他变形包括广义最小残差方法和双共轭梯度稳定迭代法,对于这方面有许多变形,但表现都很类似。
与直接求解器相反,迭代方法会逐步求解,而非通过一个计算强度很大的步骤来实现。因此,当利用迭代方法求解一个问题时,您会观察到求解过程中的误差估计会随着迭代次数的增加而减少。对于良态问题,应为单调收敛。如果您正在处理一些非良态问题,收敛就将更慢。迭代求解器的振荡行为通常表明问题没有设定好,比如问题没有足够的约束。下方显示了迭代求解器的典型收敛图:
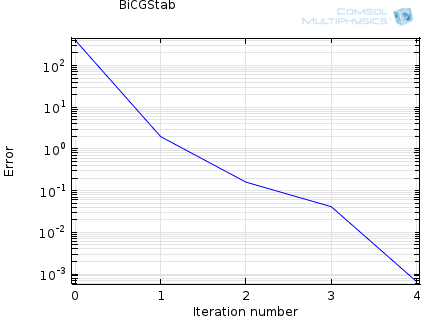
缺省情况下,我们认为当迭代求解器的估计误差小于 10-3 时,模型已收敛。这可以在求解器设定窗口中控制:
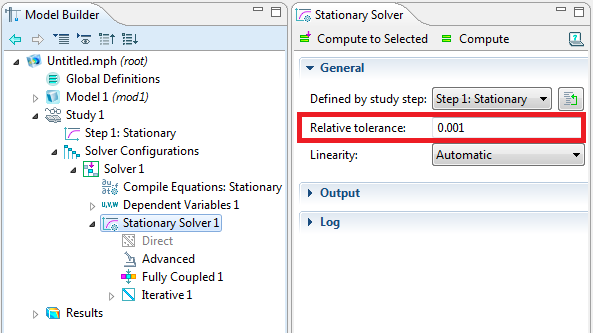
可以将容差设得更高,更快地完成求解;或者设得更低,在当前网格上实现更高的准确度。根据机器精度 (2.22×10-16) 和条件数(依赖于问题),容差必须始终大于一个数。但通常没必要将容差设得过低,因为模型的输入项,比如材料属性,其精度通常不会超过几位有效数字。如果您要更改相对容差,我们通常建议将它减少一个数量级,然后对比解。请记住,您是在当前使用的网格上以更低的容差求解,更合理的做法是细化网格。
迭代求解器最大的优势是其内存使用,当求解同样大小的问题时,它们的内存使用明显小于直接求解器。迭代求解器最大的劣势在于它们并非“直接可用”。不同物理场需要不同的迭代求解器设定,具体基于所求解的控制方程的性质。
幸运的是,COMSOL 已经为所有预定义的物理场接口内置了缺省的求解器设定。COMSOL 将自动检测要求解的物理场,以及问题大小,并针对具体问题选择求解器,直接或迭代。COMSOL 会根据最高鲁棒性和最低内存使用来选择缺省的迭代求解器,不需要用户进行任何操作。
有关直接和迭代求解方法的结束语
当在仿真中求解线性方程组时,COMSOL 会自动检测最佳求解器,无需用户进行任何操作。直接求解器使用的内存要高于迭代求解器,但更具鲁棒性。迭代求解器会逐步求解,如果需要,可以修改收敛容差。





评论 (9)
吉冬 李
2020-09-14thanks
Cris
2021-09-23您好,我的显示:找不到解,达到牛顿最大迭代次数。返回的解不收敛,没有返回所有参数步长是什么原因呢? 求解答
Qihang Lin
2021-10-08 COMSOL 员工您好,找不到解的报错可能由许多原因导致,时间步长过大、材料参数突变等都有可能导致模型在该部分不连续导致该问题的发生,您可以从物理量的时间连续性和空间连续性方面逐级排查导致您模型不收敛的原因。各个物理场导致不收敛的原因各不相同,建议您观看系列培训视频加深对您使用的物理场的理解:http://cn.comsol.com/video-training
Junliang Lin
2022-01-17i am studying finite element method, when i tried to write a program on solid mechanics in Fortran language, i used pardiso solver, but the csr format storage took a lot of time. i see that there is pardiso solver in comsol too, and it is the fastest solver. i wonder what your stiffness storage algorithm is that make it so fast.
喆 王
2023-09-24您好,在使用迭代求解器求解时,显示“使用共轭梯度求解线性方程组时,发现inf或nan”是什么原因呢?该怎么解决啊?
Qihang Lin
2023-09-25 COMSOL 员工应该与具体模型设置有关,建议联系技术支持:https://cn.comsol.com/support
xy w
2023-10-08您好,在进行磁场稳态计算时,求解器共轭梯度一直在增加,计算进度卡在72%是什么原因呢?
Qihang Lin
2023-10-09 COMSOL 员工求解器一直在迭代,表示结果不一定收敛,可能是存在设置问题导致的。您可以尝试联系技术支持寻求一些调整建议:https://cn.comsol.com/support
李托夫斯基
2024-02-29您好,我在做磁流体cfd仿真,出现:
非线性求解器不收敛。
在 速度 u,压力 p:
线性迭代发散。
线性求解器有错误消息。
严重病态预条件器。
时间:1.004280520751068e-05。
最后一个时步不收敛。
我尝试减小容差以及设置了每次迭代中雅可比矩阵更新,但是仍然作用不大,我推算可能是因为模型压力p变化过快导致的,请问有什么解决方法吗?
感谢解答