
这篇博客,我们将介绍 COMSOL Multiphysics 中求解多物理场有限元问题的两类算法。到目前为止,我们已经学习了如何进行网格划分,以及求解线性和非线性单物理场有限元问题,但是还没有考虑过同一个域内存在多个相互影响的不同物理场的问题。
一个简单的稳态多物理场问题
我们先来看一个非常简单的稳态多物理场问题:穿过金属母线板的稳态电流场,母线板内的热量传递和结构变形的相互作用。电流引起电阻加热,从而导致母线板受热并开始膨胀。因为升温较为显著,所以母线板的电、热以及结构材料的性能变化不能忽略。我们希望求出稳态条件下的电流、温度场、变形以及应力。下图为待求解问题的示意图:
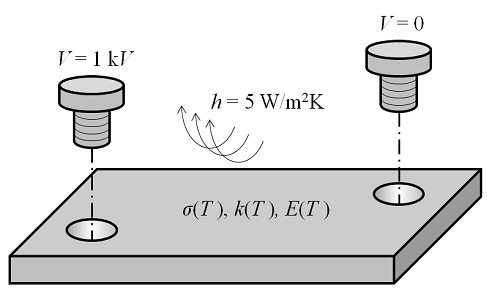
待求解的多物理场问题。
涉及的方程
这里我们需求解三个本构偏微分方程。首先,描述域内电压分布的方程为:
通过有限元法离散后,可以得到一组等式:
其中,下标 _{V} 表示未知电压,系数矩阵 \mathbf{K}_V 与未知温度 \mathbf{u}_T 相关。假设电压分布已知,体电阻热可由下式推导:
其中,电场 \bf{E} 为 -\nabla V 。这个热源出现在温度的本构方程中:
并给出了方程组:
当求出域中的温度分布后,就能求解结构位移:
其中,弹性矩阵 \bf{C} 由与温度度有关的杨氏模量 E(T) 推导。产生的热应变为 \epsilon_{\Delta T} = \alpha(T-T_0) ,应变为 \epsilon = 1/2 [{\nabla \mathbf{u}^\mathbf{T}_D + \nabla \mathbf{u}_D}] 。求解结构位移的方程组可以写成:
其中,下标 {_D} 表示未知位移。
合并以上方程组可得:
\left\{
\begin{array}{c} \mathbf{f}_V \\ \mathbf{f}_T \\ \mathbf{f}_d \end{array}
\right\}
=
\left[
\begin{array}{ccc}
\mathbf{K}_V(\mathbf{u}_T) %26 \mathbf{0} %26 \mathbf{0} \\
\mathbf{0} %26 \mathbf{K}_T(\mathbf{u}_T) %26 \mathbf{0} \\
\mathbf{0} %26 \mathbf{0} %26 \mathbf{K}_D(\mathbf{u}_T)
\end{array}
\right]
\left\{
\begin{array}{c} \mathbf{u}_V \\ \mathbf{u}_T \\ \mathbf{u}_D \end{array}
\right\}
–
\left\{
\begin{array}{c} \mathbf{b}_V \\ \mathbf{b}_T(\mathbf{u}_V) \\ \mathbf{b}_D(\mathbf{u}_T) \end{array}
\right\}
\]
为了简化方程,我们可以省略参数中的下标:
这就是求解多物理场耦合问题的所有模式!求解单物理场非线性问题和求解多物理场问题并没有概念上的区别。我们已经学习了关于求解非线性单物理场问题的所有知识,包括所有关于阻尼、负载和非线性加速以及网格划分的讨论,这对于求解多物理场问题同样有效。
全耦合法
但是,理解上述方法有一个缺点(在某些情况下是非常致命的)。通过代入 Newton-Raphson 迭代法,我们要求解导数 \mathbf{f'(u}^{i}),即:
=
\left[
\begin{array}{ccc}
\mathbf{ K}_V%26\mathbf{K}_{V,T}%26\mathbf{0} \\
\mathbf{-b}_{T,V}%26\mathbf{ K}_T%26\mathbf{0} \\
\mathbf{0}%26(\mathbf{K}_{D,T}-\mathbf{b}_{D,T})%26\mathbf{K}_D
\end{array}
\right]
这里,我们使用了一个简化符号来简化和缩短表达式,例如:
很明显,以上矩阵为非对称矩阵,这将导致一个问题:如果系统矩阵不能确定,我们可能需要使用更加消耗内存的直接求解器求解。(尽管迭代求解器在预条件选择正确的情况下能处理范畴更为宽广的问题,但并不能保证足以应对所有特例。)使用直接求解器求解此类多物理场问题将会耗费更多的内存和时间。
不过,还有一种替代方法。上述求解方式被称为全耦合法,假设需要同时考虑物理场之间的所有耦合。实际上,在求解很多类型的多物理场问题时,我们可以忽略这些非对角线的项,采取更节约内存、更具时效性的分离 求解法。
分离法
分离法按顺序分析每一个物理场,使用之前求解物理场得到的结果来得到一个待求物理场的载荷和材料属性。因此,对于上面这个例子,我们先通过 Newton-Raphson 迭代求解电压:
其中对于第一次迭代,我们必须对电压和温度各做出一个初始估计值 ( \mathbf{u}_V^{i=0} , \mathbf{u}_T^{i=0} )。使用温度场的初始条件来求解得到初始的材料性能。接下来求解温度:
其中,在第一次迭代 i=0 中 ,使用温度场的初始条件对材料性能 \mathbf{K}_T(\mathbf{u}_T^{i=0}) 求解,但是荷载是通过之前计算的电压 \mathbf{b}_T(\mathbf{u}_V^{i=1}) 计算得到。按照类似的方法,可以求解位移场:
其中,结构载荷以及材料性能是由之前计算的温度场推导而来。
继续使用迭代:有序地重复计算电压、温度和位移。 像这篇博客中定义的一样,此算法将持续进行直到达到收敛为止。
这个方法最大的优势是可以在每一个子步骤中使用最优求解器。这不仅意味着将在每一个子步求解更小的问题,还可相应的选择更节约内存的快速求解器。虽然分离法一般需要更多的迭代步骤才可收敛,但是与全耦合法中的迭代相比,分离法的每一次迭代在计算时间上都会显著减少。
如下为使用分离式求解器处理一个具有 n 个多物理场模型的算法:
- 设定模型中所有物理场的初始条件
- 初始化记录迭代次数的计数器
- 以分离法的求解顺序求得解一个物理场,使用上一步骤计算材料性能
- 利用已求解的扑粉解求解第二个物理场
- …
- 使用之前计算的第(n-1)个解求解第 n 个物理场
- 重复步骤 2-6 直到收敛,或迭代次数超过预期峰值
对于一般物理场问题,用户仍然需要确定物理场的求解顺序,但是软件会默认建议内置的多物理场接口使用合适的求解顺序。 COMSOL Multiphysics 会按照分离法的求解顺序为每一个物理场提供默认的线性求解器设定。
使用分离法得到的收敛解与使用全耦合法得到的解完全一致。通常分离法会经过更多次的迭代以达到收敛,但是每个子步骤的所消耗的内存和时间会降低,从而进一步降低整体的求解时间和内存使用率。
求解多物理场问题的总结
在这篇博客中,我们介绍了处理多物理场问题的两类算法:全耦合法 和分离法 。全耦合法与求解单物理场非线性问题的 Newton-Raphson 迭代法一样,非常占用内存,但是十分实用,广泛适用于存在强相互作用的多物理场问题。另一方面,分离法假设能对每一个物理场单独求解,并且能在多种物理场之间完成迭代直至模型收敛。



评论 (3)
欣润 吕
2018-08-13请问”全耦合法”下面的”f(ui)”是否应改为”f'(ui)”?
此外f'(ui)的矩阵表达式中,第一行第二列是否应改为KV,T · uV ? (即是否漏掉了uV);
以及第三行第二列是否应改为 KD,T · uD-bD,T ?(即是否漏掉了uD)。
谢谢!
Kaixi Tang
2023-03-20 COMSOL 员工你好,对于你提到的问题,我理解博客中的相关公式是没有问题的。
具体来说,对于你提到的的矩阵,其表示的是f(u)求导,而非是对其求逆:其中第一列,表示的是三个控制方程依次对“uv”求导;第二列表示三个控制方程依次对“uT”求导;第三列亦然。比如你提到的第三行第二列,对应的是力学控制方程对“uT”求导,所以得到的是KD,T-bD,T(KD、bD与uT有关,遵循链式法则)。
Tengyue Gao
2018-10-19吕欣润,您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!