
COMSOL Multiphysics® 软件提供了许多内置的物理方程和接口,但部分仿真问题需要在软件中添加非内置的物理场进行求解。拥有出色的灵活性的 COMSOL® 软件支持添加用户定义方程,并基于方程进行建模。今天,我们将讨论如何利用基于方程的建模来求解浅水波动方程,并将其用于分析海岸侵蚀问题。
使用浅水波动方程分析海岸侵蚀问题
在海岸线上,海浪冲击和永不止息的潮汐运动导致了海岸侵蚀,这种现象会带走海滩上的沉积物,并磨蚀土地。

受海岸侵蚀影响的岩层。图像由 John Nuttall 提供。在 CC BY 2.0 许可下使用,通过 Flickr Creative Commons 发布。
虽然海岸侵蚀可以带来一些好处,例如在沙滩上产生的泥沙,然而更多时候它会给沿海居民的财产和住房带来严重的损失。为了有效预测这种危害,研究人员可以使用浅水波动方程来深入研究海岸侵蚀的过程。科学家能够利用方程模拟海洋和大气流体流动,进而预测哪些地区将受到海岸侵蚀、极地冰盖融化和污染等问题的影响。
相较于 Navier-Stokes 方程出错与否很大程度上取决于自由表面的解析情况和建模域的尺度,浅水波动方程更有优势。下面,我们将重点演示如何使用基于方程的建模功能来求解浅水波动方程。
在 COMSOL Multiphysics® 中求解浅水波动方程
在浅水波动方程模型中,我们可以添加自己的方程来描述物理场——即所谓的基于方程建模的功能。我们使用一般形式偏微分方程 接口和两个因变量来简化建模流程。通过这种方式,我们能方便地将表达式定义为模型变量,因为在定义初始波形时模型变量大有用处。
这个简单的一维模型使用了 Saint-Venant 浅水波动方程来研究变化的海床上的波浪随时间逐渐平静的过程。
此案例中的一维模型需要大量工作才能转换成二维模型,以便求解典型的应用问题。因此,本教程是一个展示基于方程建模优势的实用案例。
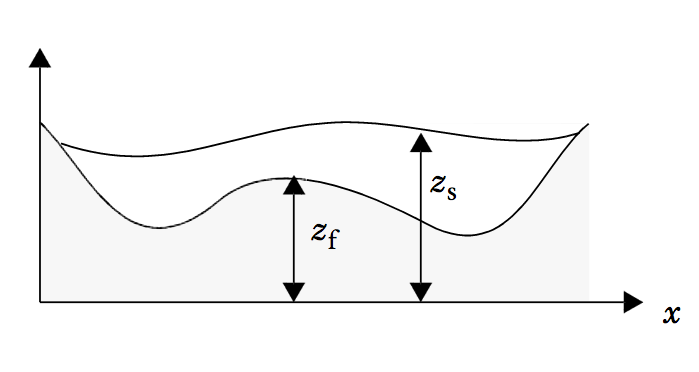
流体域的垂直部分。其中 zf 是海床剖面的解析表达式, zs 是水面的剖面。
模型研究了通道内的浅水波动,其两端均设置了约束条件,并以波形为初始条件。为了方便改变波的振幅和海床形状等参数,我们可以用数学关系来描述初始波和海床的形状。请注意,模型在 x 方向和 y 方向上的尺度有所不同,如下图所示。
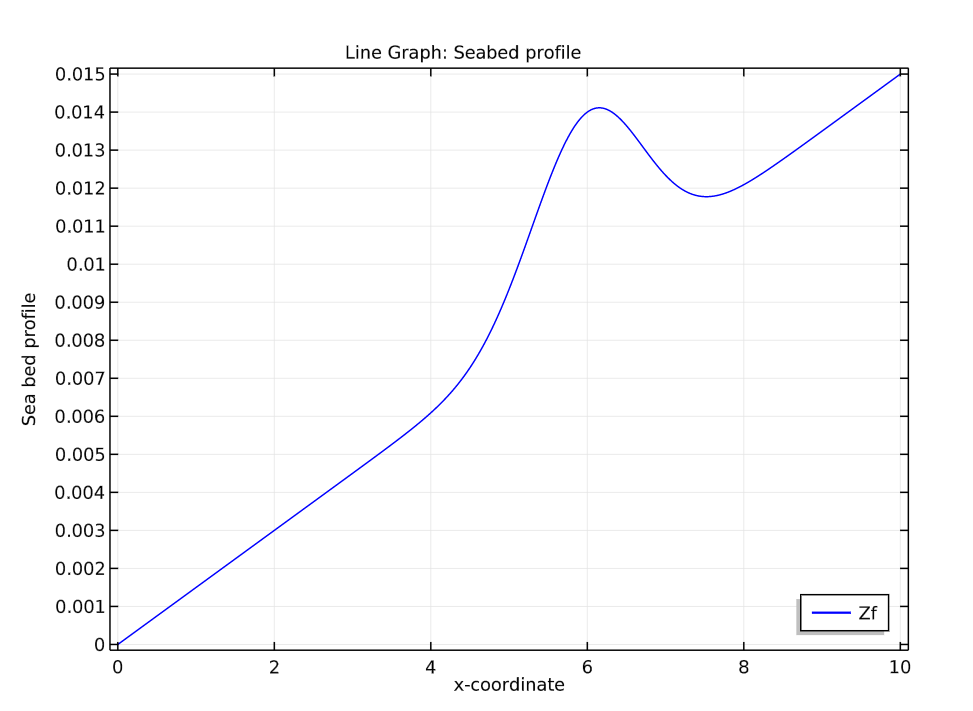
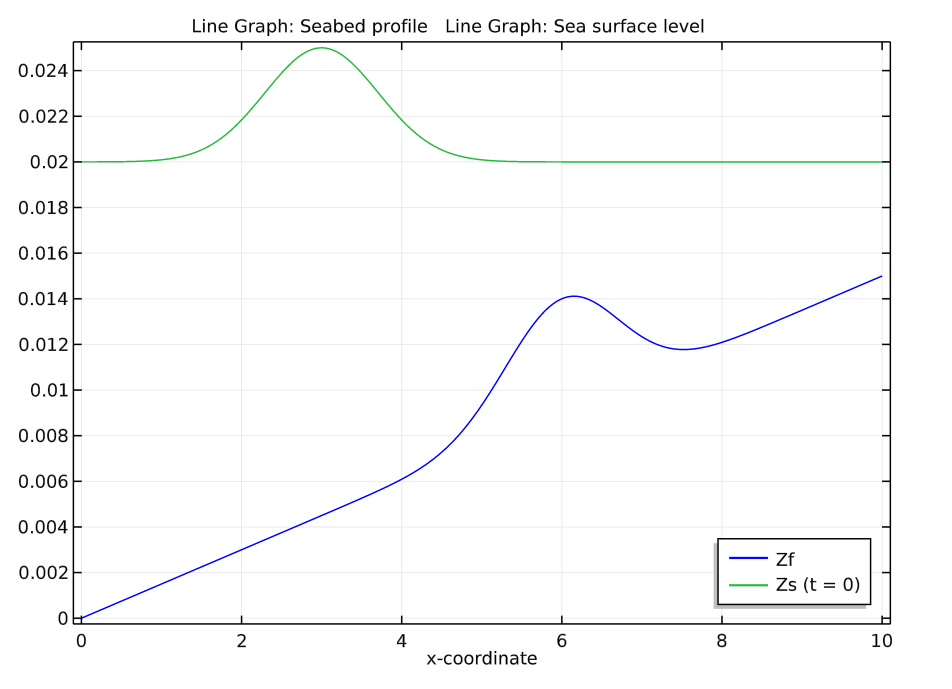
海床剖面图(左)以及初始水面剖面与海床剖面的比较图(右)。
可以看到,随着时间推移,流体的流动阶跃不连续性不断发展,这会导致解的不稳定性。为了使解稳定,我们可以添加一个人工粘度,使单元雷诺数的阶次统一。将流体的阶跃被替换为可在网格上求解的陡峭斜面。
现在我们来看看模拟结果。在仿真运行了 60 秒后,我们可以看到从仿真开始后 15 秒的时间内,6 个不同时间点上的水面和海床坡度。
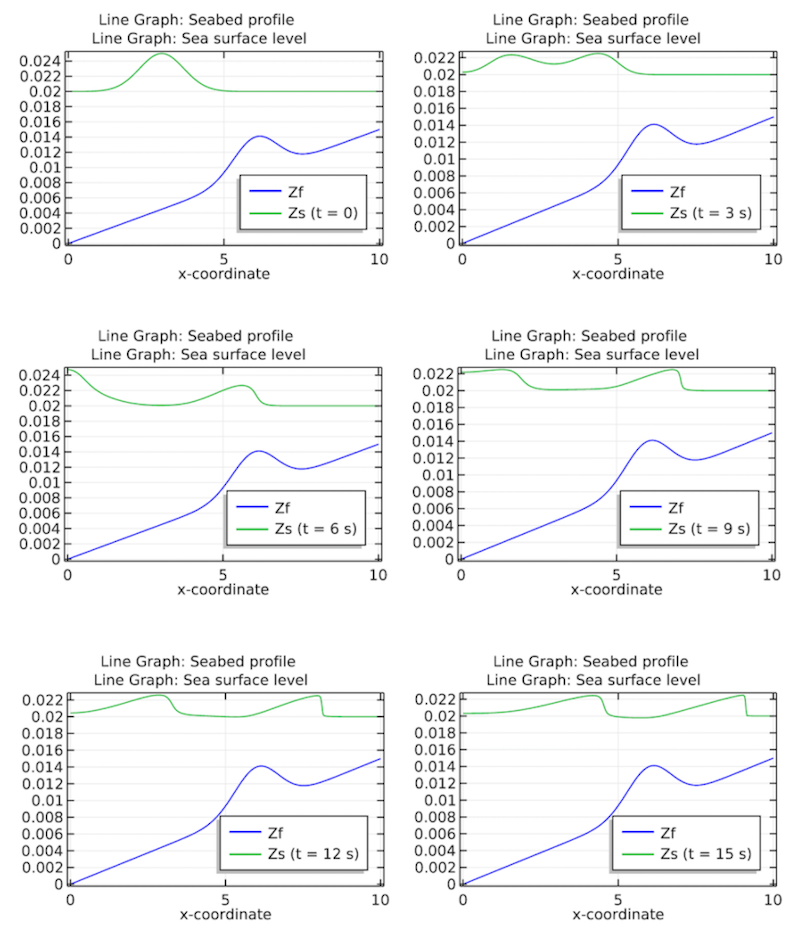
海床剖面绘图显示了水位 3 秒内的增加情况。
以上结果清楚地表明,海床的几何形状会影响水面的高度,而水面高度会继而影响海岸侵蚀的效果。
我们可以通过创建和导出动画生成可视化的仿真结果,并与其他人分享这些自定义结果——这也是 COMSOL Multiphysics 的一个功能亮点。
仿真结果的动画。
快快点击下面的按钮,亲自操作此教程吧。






评论 (0)