
如果你正在使用有限元仿真软件(例如 COMSOL Multiphysics),就会在某些时候遇到“弱形式”这一表述。这个时候,你可能会想知道这个表达是什么意思?实际上,弱形式是一个非常强大的概念。今天,我们将带您了解它的基本思想和使用它所带来的好处。
弱方程的起源
多物理场仿真是基于偏微分方程 (PDE)建立的。这些偏微分方程通常来自物理原理的守恒定律,例如质量、能量和动量守恒。这些众所周知的守恒定律可以在没有任何进一步假设的情况下,被表述为任意域上的积分方程。
体积积分项描述的是域内存储的或由源添加的内容,而表面积分描述的是与相邻域或外部环境的相互作用。假设所有涉及的函数都足够平滑,高斯定理可以将表面积分转化为体积积分。由于推导中使用的域是任意的,因此所得方程必须在每个点上都是独立有效的,从而将积分方程转化为偏微分方程。
然而,在这个标准的偏微分方程推导过程中存在一个小小的缺陷:即所涉及的函数(特别是材料属性)并不总是足够平滑,从而使方程在某些地方不满足高斯定理的使用条件。由于产生的偏微分方程无法满足在所有物理意义上的合理性,因此称该微分方程过于严格(这就是弱形式发挥作用的地方)。为了返回一个比偏微分方程严格程度低的积分公式,弱方程部分地反转了推导过程。这意味着弱方程实际上比经典方程更接近基础物理学。
如何从经典方程推导出弱方程
我们将从偏微分方程开始,并概述导出其弱对应项的典型过程。为此,我们考虑一个扩散方程:
COMSOL 软件中的大多数方程都包含相似的项。对于传热应用,扩散系数 c,以及源项 f,分别指导热系数和热源。如果未知函数 u, 是原偏微分方程的解,也是以下积分方程的解:
其中,v 为任意函数,在偏微分方程两侧相乘 v 后,等式两侧分别在域 \Omega 上积分。
反之,如果该积分方程对于足够数量的任意函数 v 都成立,那么 u 可能是原微分方程的解。这就是为什么函数 v 被称为试函数,在有限元方法中起着关键作用。我们将在下面部分讨论如何选择试函数。
将偏微分方程转换为这个积分方程已经反映了弱形式的性质,但通常还需要进行第二步。这个步骤将高斯或格林公式的散度定理(也被称为部分积分)应用于二阶导数。在我们的例子中,我们可以将前面的积分方程的左侧改写为:
其中,\partial \Omega 为域 \Omega 的边界,n 为指向域外侧的法向量。使用这个公式,扩散方程的最终弱形式如下:
边界积分负责与周围环境 \Omega 相互作用。在这里,边界条件开始发挥作用,它描述了这种相互作用,从而使整个方程具有唯一解。当我们模拟传热时,-c\nabla u\cdot n 项描述了边界上的热通量。例如,如果没有热通量,那么边界就是绝热的。
试函数的选择
如果一个函数 u 能求解许多不同试函数 v 的弱方程,则称为偏微分方程的弱解。更确切地说,我们不仅要考虑一个 试函数,v 代表一系列试函数,其中每一个试函数都对应一个方程。当然,我们不可能考虑所有可能的试函数,因为这将导致无限多的方程。在实践中,我们需要一些经过精心挑选的试函数。这就是有限元发挥作用的地方。
大家都知道,在运行研究之前需要对计算域进行网格划分。网格划分将几何体划分为一组更小的体积——单元。然后可以在每个单元上使用多项式定义试函数,该试函数只在一部分相邻单元上非零,以外为零。以这种方式构造的最常见的多项式类型被称为 拉格朗日形 函数,COMSOL 软件的许多物理场接口都使用了这个函数。
选择离散化(左)。 在离散化设置中,默认使用拉格朗日元素(右)。
当然也有其他可能的试函数存在,但我们在此不讨论这些细节。需要注意的是,由于与不同网格单元相关的试函数是独立的,所以网格有效地决定了试函数的数量,以及它们的空间分辨率。
上述所有这些与你的解有什么关系?你的计算结果实际上是所有相关试函数的叠加。也就是说,尽管你的真实解可能是一个相当复杂的函数,但它可以被近似为非常简单的函数组合。网格越细,包含的形状函数越多,求解效果就越好(尤其是在梯度陡峭的区域,因为需要更多的网格单元)。如果继续细化网格,直到解不再发生变化,你就成功地执行了网格无关性分析,你的解很可能是原始偏微分方程解的良好近似。
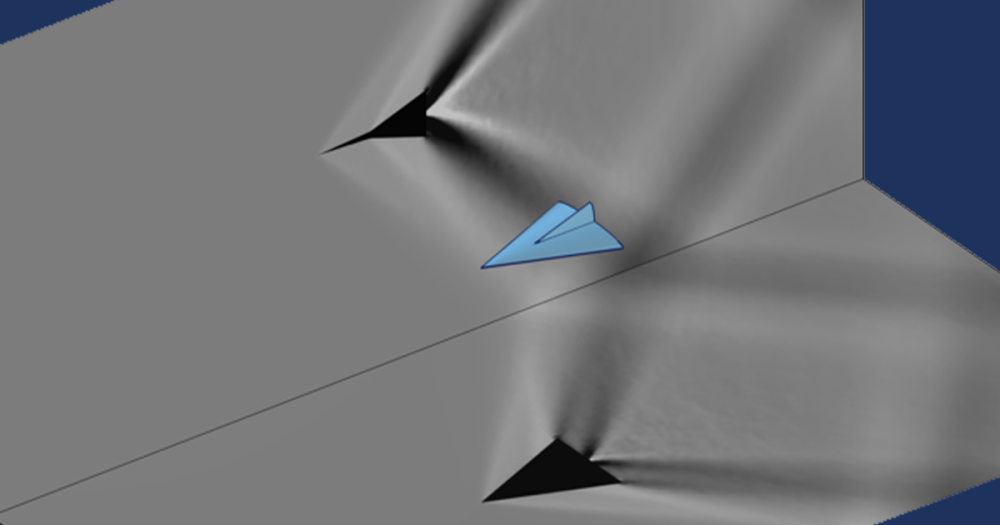
这种使用试函数来近似求解的方法被称为 Ritz-Galerkin 方法,从某种意义上说,它是最好的有限元方法,因为它能使计算结果和精确求解的误差最小。关于离散化的主题还有很多要讨论的内容,比如网格划分和收敛。现在我们添加下面的图,它可以代表一个给定载荷下的弯曲膜。它显示了随着网格分辨率的增加,解的分段线性近似。
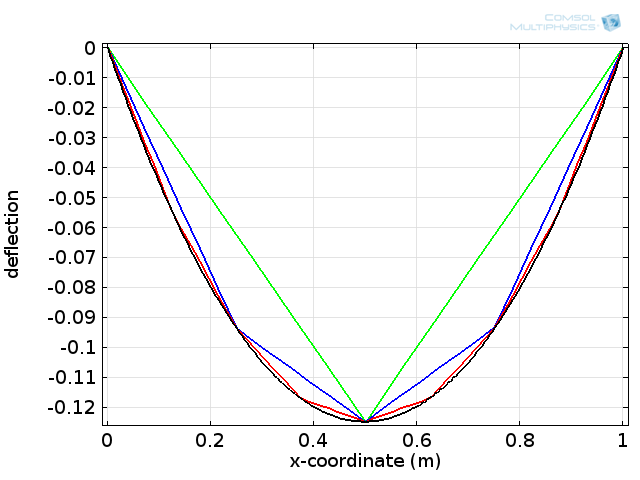
增加线性形函数数量可对解进行优化
数学极限会发生什么?
理论上,网格分辨率可以进一步提高,这意味着试函数集将变得更大。可以想象,这个过程的数学极限导致了一组在某种意义上完整且连续的试函数。从实践的角度来看,这并不相关,但这个论点产生了一个可解性和解的唯一性的合理数学理论。虽然作为 COMSOL Multiphysics 的用户不需要处理这些问题,但知道你的计算有可靠的理论基础会令人很欣慰。
COMSOL 语法中的弱方程
说到这里,你可能想知道弱形式在 COMSOL 语法中是如何表达的。为此,软件提供了 test 算子,用于表述试函数 v。test 算子对因变量 u 及其导数进行运算,即 v=\mathrm{test}(u)。以这种方式将试函数与解相关联是有逻辑的。如上所述,如果解在网格上使用多项式基表示,则对试函数使用相同的基可以确保离散系统包含相同数量的未知数和方程。
为了将示例中弱方程的第一项转换为 COMSOL 语法,我们首先需要通过 x、y 和 z 的偏导数来重写梯度。这里,一阶偏导数记作 \frac{\partial u}{\partial x}=ux。
类似地,试函数的偏导数表示为 \frac{\partial v}{\partial x}=\mathrm{test}(ux)。
以此,弱形式的域积分项在 COMSOL 语法中被读取为:
边界项需要特殊处理,这超出了本文讨论的范围。因为弱形式 偏微分方程 会自动设置为零,因此不需要包含等号。需要注意的是,这种转换通常是自动完成的,因为 COMSOL Multiphysics 需要弱形式来推进计算。此外,用户也可以自己输入弱形式。默认的弱形式 PDE 接口作用在域上,其中 c=f=1,并且包含一个正负号变化,如以下屏幕截图所示:
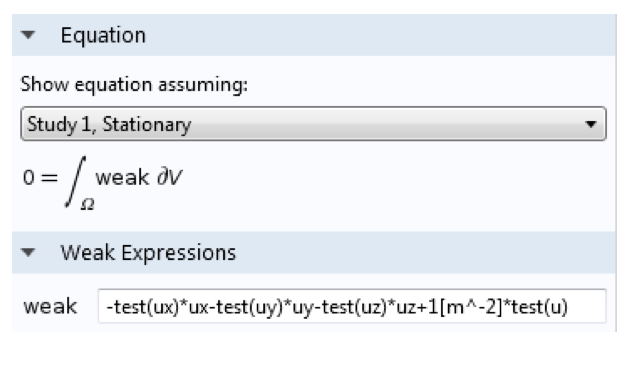
COMSOL Multiphysics 中可用的弱形式接口(左)。 如何在 COMSOL 语法中输入弱形式的示例(右)。
弱方程的优势
所有这些在实践中意味着什么?现实世界并不总是美好而顺畅的。它可以显示材料数据、粗糙表面、点源以及溶液的快速变化或其梯度。虽然经典 PDE 达到了非光滑物理效应的极限,但弱方程通常是非常合适的。它们不太严格,因为所有涉及的项都是网格单元上的积分,不需要在域中的每个点都明确定义。这是有限元方法的主要优势,它使 COMSOL 软件和用户能够获得真实世界应用的解。
总结一下,弱方程:
- 是积分方程组的集合。网格决定了研究中求解的方程的数量。
- 允许为真实世界建模,因为它们都源自潜在的物理守恒定律。
- 提出一个关于可解性和解唯一性的可靠性数学理论。




评论 (2)
若倩 林
2024-02-27您好,请问弱贡献-2test(T)替换成狄拉克雷边界条件-2(或者2,2testT等),计算出结果不一样,并且前者lambda为-2,后者为-1.75。
Kaixi Tang
2024-03-11 COMSOL 员工您好,对于狄式边界设置为u=-2后,如果要把它写成拉格朗日乘子的形式,首先需要尝试在弱贡献中添加辅助因变量,比如lambda。之后在对应表面输入弱贡献表达式:-test(lambda)*(u+2)-lambda*test(u)。当然,也可以直接使用弱约束,软件自动定义上述步骤。