解析瞬态波

问题描述

我正在求解一个瞬态波型问题，应该调整哪些网格和求解器设置才能获取更高精度并缩短运行时间？

解决方法

对于求解电磁、声学、结构或任何其他波型模型的瞬态模型来说，其精度受限于两点：有限元网格在空间中对波的解析程度以及时步对时间变化的解析程度。本文介绍在分析此类问题时如何控制网格和求解器设置。

注：如果您使用时域显式公式（例如压力声学，时域显式、弹性波，时域显式、对流波动方程，时域显式或电磁波，时域显式物理场接口）求解模型，那么本知识库条目并不适用。在使用这些接口时，请参考文档中关于网格和求解器设置的建议。

在开始建模之前，您应该知道以下两点。首先是激励的最大频率组成。您需要将其定义为全局参数，如：f_max。其次是所有域的材料属性。由于材料属性控制可能出现的最短波长，所以此信息控制所有域中需要使用的网格大小。如果任何材料或边界条件具有非线性，请注意这可能产生倍频，或引起可能导致更高频率组成的其他现象。如果您预计载荷或边界条件将发生任何阶跃变化，请先阅读：知识库 1244：求解载荷呈阶跃变化的波型问题。

在知道预期建模的最大频率和材料属性后，您便可以构建模型并进行网格划分。默认情况下，电磁、声学和结构瞬态接口中使用二阶（二次）单元。网格至少必须满足奈奎斯特准则，因此每个域中的每个局部波长至少有两个单元。但是，这通常会产生令人无法接受的低精度。实际上，每个局部波长应至少使用五个二阶单元，但每个波长很少超过十个单元。您可以设置用户控制网格，对不同的材料域应用不同的大小特征。您可以首选使用自由三角形网格（对于二维模型）和自由四面体网格（对于三维模型）；但如果模型的结构具有较大的长宽比，包含薄层，材料呈各向异性，或者您出于其他原因期望解仅在一个或两个方向发生明显变化，则可以使用其他单元类型（六面体、三角柱和金字塔单元）。压力声学，瞬态接口支持的 PML 应使用映射或扫掠单元。此外，还需定义全局参数（例如：N）来控制每个局部波长的单元数，并定义一组变量来定义不同域中的局部波长，如下面的屏幕截图所示。

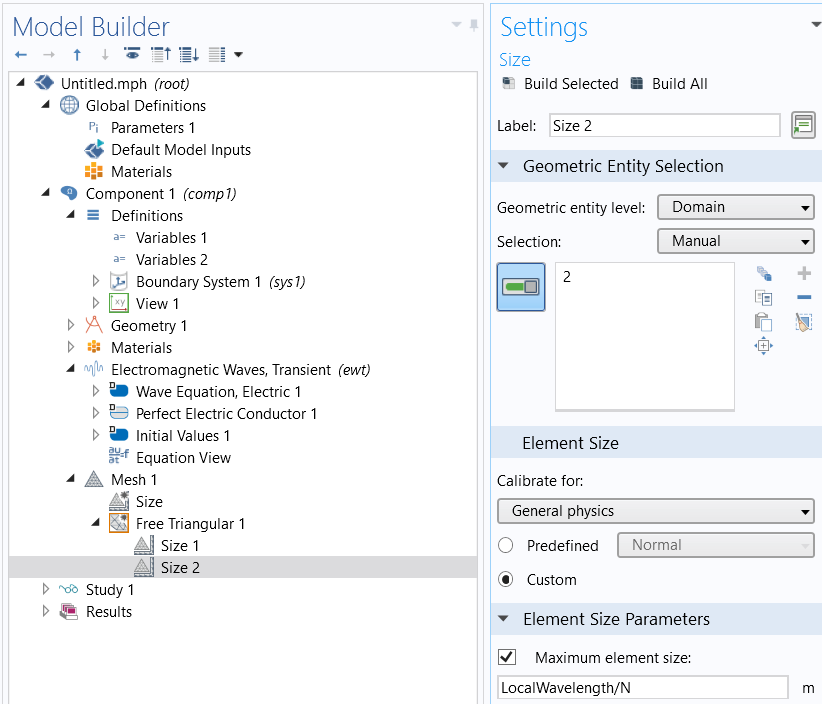
手动设置单元大小

请记住，在结构力学中，不同类型的波具有不同的波长。在本体材料中，剪切波的波长通常比压力波短。但是，例如在较薄的几何部分，弯曲波甚至可以更短。由于您无法始终预先知道确切的波长，因此，请务必检查求解结果 - 解看起来是否平滑？是否得到了适当的解析？- 如果有任何疑问，可以考虑运行网格收敛性研究。

对于大多数接口（瞬态压力声学、热黏性声学和气动声学接口是显著的例外），默认情况下，瞬态求解器会不断调整时步，以满足您指定的容差。“瞬态”设置中的相对容差框（如下所示）控制求解器如何调整时步。这个数值越小，时步就越小，精度就越高。请注意，更改瞬态节点中输出时步的数量仅控制输出时步，而对求解器实际采用的时步几乎没有影响。

输出时步和相对容差设置

然而，由于您已经知道最大局部网格大小和最大频率，因此手动设置时步在计算上更高效。该时步在时域解析波应与网格在空间中进行解析的效果一样好。较长的时步不能最佳利用网格，任何较短的时步都会导致求解时间较长，而结果并没有明显的改进。波速 c、最大网格大小 h 与时间步长 Δt 之间的关系称为 CFL 数：

CFL = cΔt/h

我们已将最大网格大小手动定义为局部波长的 1/N（如上所述），因此可以根据频率 f 和每个局部波长的单元数 N 将上述关系重写为： CFL = fNΔt

重组后得到：

Δt = CFL/Nf

使用默认的二阶（二次）网格单元后，CFL 数应小于 0.2，并且值 0.1 被证明接近最优，将 CFL 数也定义为全局参数会很有帮助。

对于前面提到的声学接口，默认情况下已设置瞬态求解器，从而支持手动调整时间步进，并考虑了 CFL 数。为了使求解器采用合适的时步，请在物理场接口节点的设置选项卡中为要求解的最大频率输入已定义的 fmax 。这会生成一个手动时步 1/(60*fmax)，如果每个波长使用 6 个单元进行网格划分，则对应的 CFL 数为 0.1。

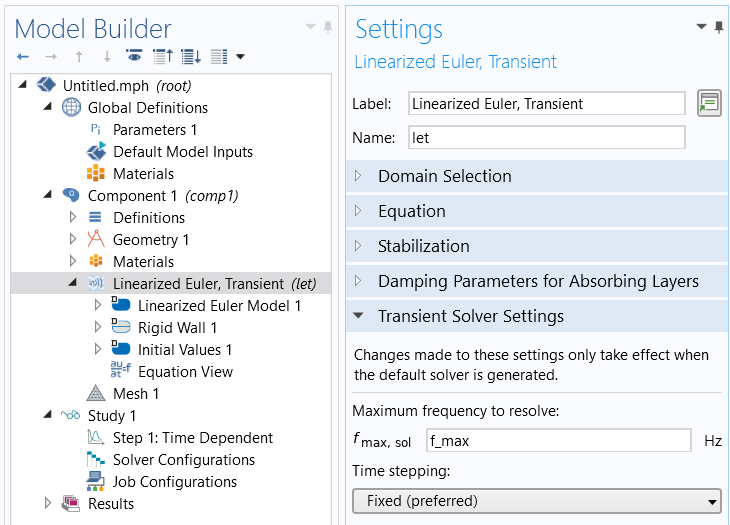在瞬态声学接口中设置要求解的最大频率

对于其他接口，您可以在瞬态求解器设置中实现手动调整时间步长，通常可在“研究 > 求解器配置 > 解 > 瞬态求解器”的“时间步进”栏中进行设置。（如果“研究”分支中没有这些设置，您可以右键单击研究并选择显示默认求解器。）将时间步进下的方法：设为广义 α，求解器采用的步长：设为手动，并将时步设为： CFL/(N*f_max)

首选使用广义 α 求解器的原因请参见知识库 1062：向后差分公式法、广义 α 法和龙格-库塔法

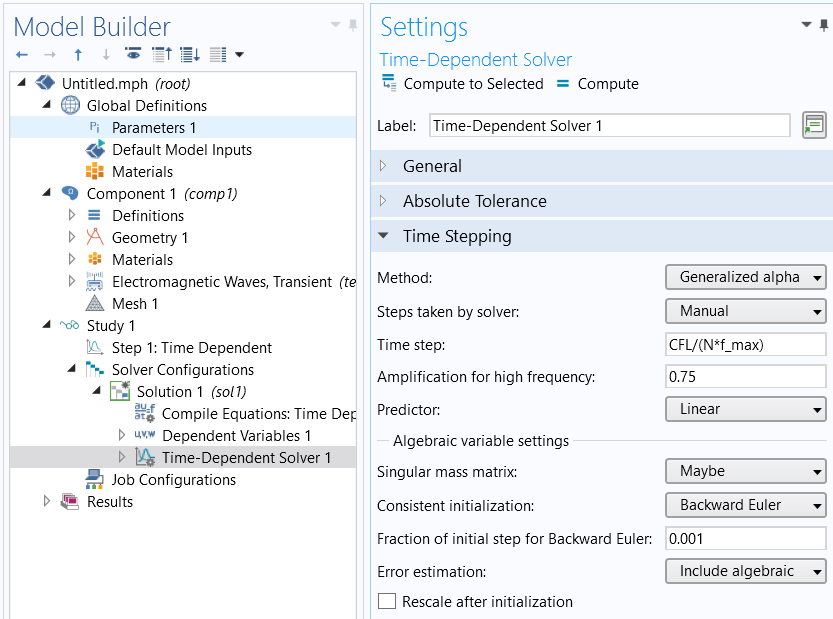
手动设置时间步长

有关这些网格和求解器设置的示例，请参见“声学模块”案例库中的高斯爆炸波。

有关在“RF 模块”中对非线性材料建模的示例，请参见高斯光束的二次谐波产生。“波动光学模块”也提供了相同的示例：高斯光束的二次谐波产生

另请参见：

知识库 1244：求解载荷呈阶跃变化的波型问题

知识库 1240：手动设置变量的缩放比例

按类别浏览