
当对具有特定几何结构的可延展材料样品进行拉伸试验时,会发生一种称为颈缩的现象。在一定载荷下,变形不再均匀,并形成局部“颈缩”。工程技术人员可以使用仿真来预测何时出现这种现象。在描述弹塑性金属条颈缩的基准模型中,COMSOL® 软件用于求解数值模型,其结果已经由发表的研究验证。
对弹塑性材料进行单轴试验
金属等结构材料在外力作用下容易变形或者改变其形状或尺寸。在某些材料中,如果载荷相当小,那么变形只是暂时的,材料会反弹回其原始形状。这种现象称为弹性 变形。然而,随着对同种材料上载荷的增加,变形可能是永久性的,这称为塑性 变形。呈这种行为特性的材料是弹塑性 材料。
对于工程技术人员来说,测试弹塑性材料的强度并评估其变形的可能性是非常重要的。一种方法是通过材料测试中的拉伸(拉力)测试,这是获得固体材料应力-应变关系的常用方法。
单轴测试是最流行的方法,这要归功于一种便于设计此类实验的设备:万能试验机(UTM)。这台机器的“万能”,体现在它可以对各种结构和材料实现多种测试,用途极其广泛。

延性断裂型合金的拉伸试验结果,其中可以看到局部颈缩。图片由 Sigmund 提供,在 CC BY-SA 3.0 许可下使用,通过 Wikimedia Commons 分享。
在典型的 UTM 中,使用的是平面或圆柱形试样。本例中,假设金属条由延性材料制成。如果 UTM 拉伸延性试样至断裂,那么在失效之前可以观察到金属条的厚度或直径局部减小。其结果是一种称为颈缩的不稳定现象,即材料的横截面积开始减小。
拉伸试验通常在位移控制 下进行。记录试样中的施力,由于颈缩引起的横截面减小,实质上会导致该力减小。这些控制条件很重要,因为如果试验是在力控制下进行的(例如,通过在样品上增加重量),一旦达到峰值载荷,金属条就会折断。
浅谈颈缩不稳定性背后的理论
颈缩可以出现在试样的任何位置。该位置由直径、材料特性和测试机对准情况的微小偏差控制。可以通过解析方法估计颈缩何时发生。由于在此之前会发生大的塑性变形,并且金属的塑性变形不会发生体积变化,你可以假设当前长度和当前横截面积的乘积给出了恒定的体积:
这里,下标 0 表示原始值。
因此,长度的小幅增加 dL 必须伴随着面积的微小(负)变化 dA ,使得
实际(对数)应变的增量定义为
实际的应力被定义为力除以当前面积
当力无法再增加时,颈缩开始产生。这是因为面积的减小速度快于材料的硬化速度;也就是说
因此,不稳定性标准是:
最后,我们得出了一个非常简单的准则来判断颈缩的发生:
因此,当应力-应变曲线的斜率等于(或小于)当前应力值时,就会发生颈缩不稳定性。
有趣的是,拉伸试验中的最大力用于定义材料的极限拉伸强度。然而,极限拉伸强度并不是材料的真实属性,而是综合考虑材料属性与试样几何结构组合的情况。
要对受拉伸试验的金属条中的颈缩效应进行建模,可以使用 COMSOL Multiphysics® 和附加的非线性结构材料模块。
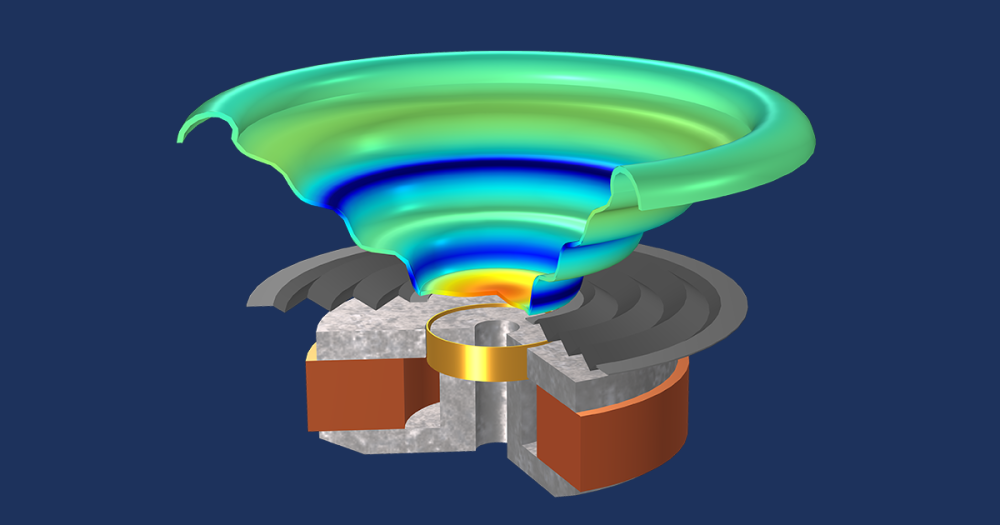
弹塑性金属条的颈缩。该仿真是根据教程模型创建的,该模型演示了 COMSOL® 软件中提供的大应变塑性选项。
用 COMSOL® 软件模拟弹塑性金属条的颈缩
在大应变塑性规范的弹塑性金属条基准示例中,你可以精确地模拟弹塑性材料中的颈缩现象及其发展,并将半径变化与文献中的结果进行比较。
在单轴试验期间,当试样上的载荷增加到一定量时,金属条会发生塑性变形,在随后的阶段,其中心横截面会出现颈缩。
该模型设置为圆柱形钢条(高度为 53.334 mm,半径为 6.413 mm),将使其伸长14mm。由于问题呈二维轴对称性,因此可以将几何结构缩小为宽度等于钢条半径的矩形。由于轴向对称,模型的高度等于钢条长度的一半,如下所示:
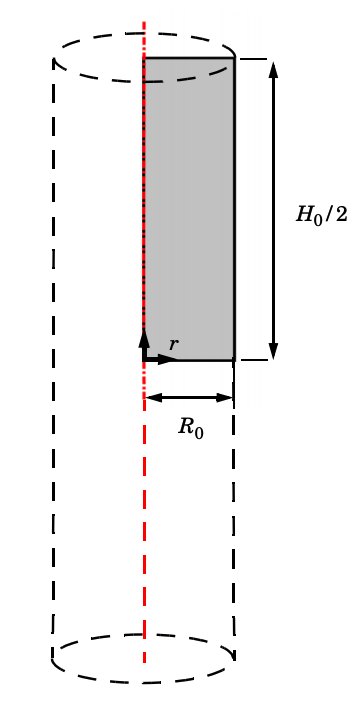
数值模型示意图;红线表示旋转对称轴。
你还可以设置径向和轴向位移的边界条件,并通过规定的伸长量施加拉伸载荷。
接下来,材料的弹性可以通过杨氏模量 E = 206.9GPa 和泊松比 v = 0.29 来表示。然后,可以使用“弹塑性金属条的颈缩”模型文档给出的常数和非线性各向同性硬化模型来设置屈服应力和硬化函数。在该图中,非线性硬化显示为等效塑性应变的函数:
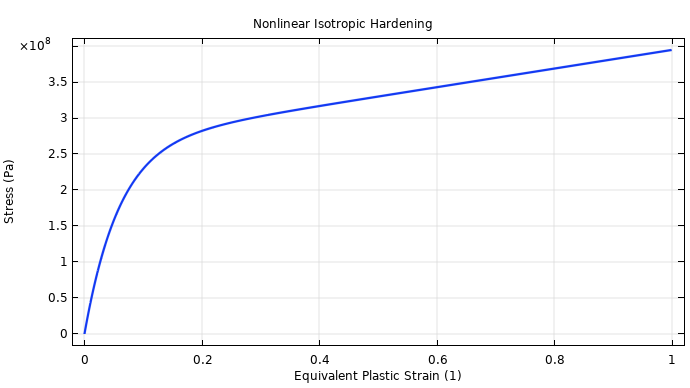
非线性各向同性硬化随等效塑性应变变化的情况。
评估仿真结果
金属条在对称平面产生较大的塑性应变之后,结果表明,14mm 的伸长量(如下图所示,我们模拟的是其一半,为 7mm)会在受影响最严重的区域产生大于 1.6(160%)的有效塑性应变。你可以看到下面这个红色区域,此处因颈缩效应金属条中的有效塑性应变呈等值线状。
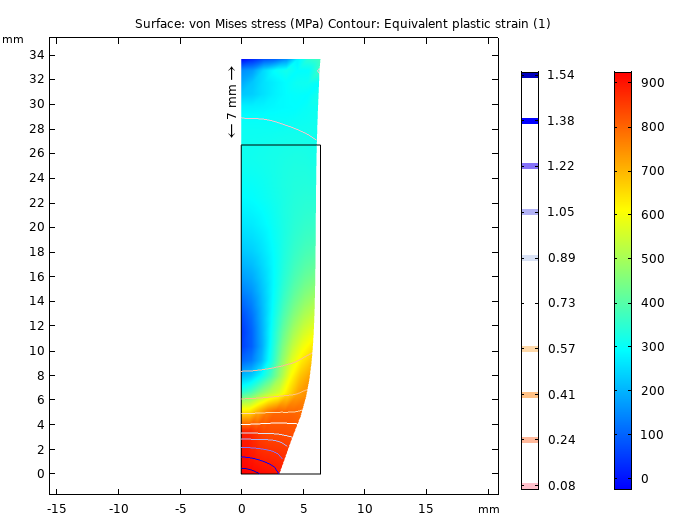
端部位移为7mm时的 Von Mises 应力和等效塑性应变。
接下来,我们来看看半径的变化。首先,半径随施加的位移线性减小。然后,当轴向位移达到3mm时,半径会急剧减小,这表明金属条正在颈缩。
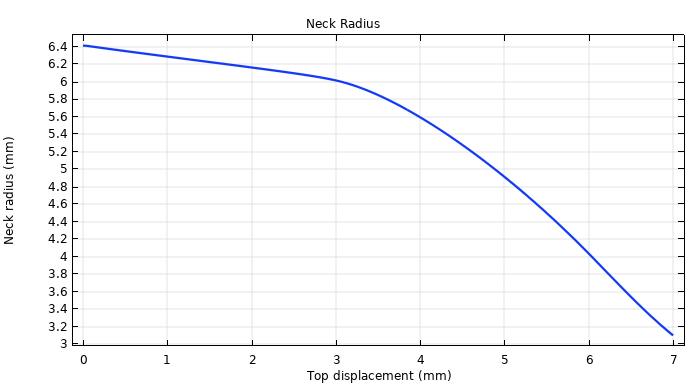
金属条中部截面颈缩的变化情况。
这些结果与已发表的研究结果非常吻合,表明 COMSOL® 软件可以精确模拟单轴试验,并能说明弹塑性材料中的颈缩现象。
后续操作
请尝试自行模拟弹塑性金属条的颈缩。单击下面的按钮将进入“案例下载”页面,你可以从中下载教程文档,并使用有效的软件许可证下载 MPH 文件。




评论 (2)
Dong Xu
2023-04-26comsol能不能仿真金属条拉伸颈缩之后断裂的模型呢?我最近看了很多关于固体力学的资料始终没有找的正确的方法,我非常希望您们能给我一些启发,谢谢!
Anran Wei
2023-05-16 COMSOL 员工在COMSOL中,可以计算某个预制裂纹的应力强度因子、J积分,判断该裂纹是否会扩展;也可以利用CZM模型、相场法,对裂纹的扩展进行仿真分析。您可以参考官网上的相关案例,看是否满足您的仿真场景需求。