
阿基米德螺线通常被用于分析电感线圈、螺旋换热器及微流控装置。今天,我们将演示如何利用解析方程及其导数建立阿基米德螺线,并借此定义一组螺旋曲线。随后,我们将基于这些曲线创建具有特定厚度的二维几何结构,并将其拉伸为完整的三维几何结构。
阿基米德螺线简介
螺线或螺旋结构在自然界中随处可见,并且被广泛应用于各类工程设计中。例如,电气工程师可能需要将电感线圈绕成螺旋形并以此来设计螺旋天线,而机械工程师在设计弹簧、斜齿轮,甚至是下图中的钟表机械时,都可能使用到螺线。

钟表结构中的阿基米德螺线示例。图像由 Greubel Forsey 提供。已获 CC BY-SA 3.0 许可,通过 Wikimedia Commons 共享。
在这里,我们将目光聚焦于一种与上图机械系统类似的特定类型螺线:阿基米德螺线。阿基米德螺线 是一种相邻两匝线圈之间的距离固定不变的螺线类型。正是这一属性,使阿基米德螺线被广泛应用于扁平线圈和弹簧的设计中。
我们可以将阿基米德螺线的极坐标方程式表示为:
其中,参数 a 和 b 分别用于定义螺线的初始半径与相邻线圈之间的距离,后者的值为 2 \pi b。请注意,阿基米德螺线有时又称等速螺线。得到这一名称是因为,从原点到相同半径与螺线的交点的距离呈等差数列。
设计参数化阿基米德螺线几何结构
大致介绍完阿基米德螺线之后,让我们看看如何在 COMSOL Multiphysics 中对此结构进行参数化,以及创建此类用于分析的设计。
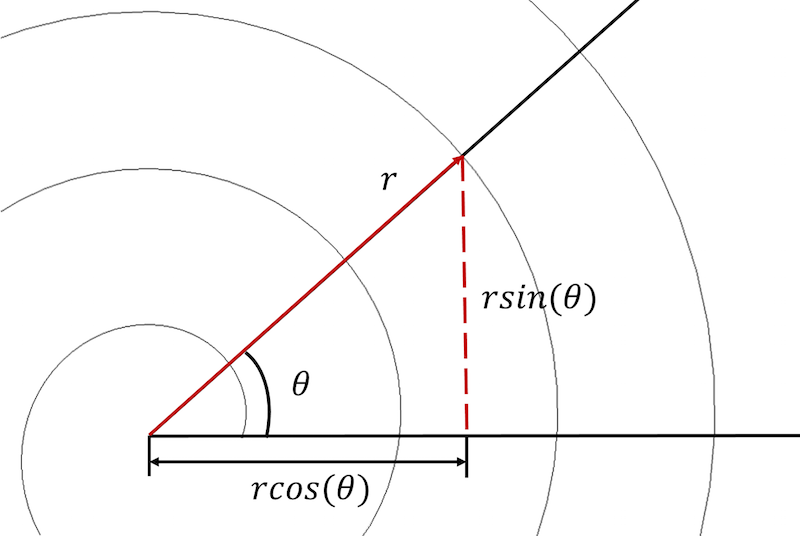
我们可以利用极坐标系和笛卡尔坐标系对阿基米德螺线进行描述。
首先,我们需要将螺线方程由极坐标系变换为笛卡尔坐标系,并将每个方程表示为参数形式:
x_{component}=rcos(\theta) \\
y_{component}=rsin(\theta)
\end{align*}
借助这种变换,我们就可以在笛卡尔坐标系中以参数形式重新表达阿基米德螺线方程:
x_{component}=(a+b\theta)cos(\theta) \\
y_{component}=(a+b\theta)sin(\theta)
\end{align*}
在 COMSOL Multiphysics 中,我们必须确定一组用于定义螺线几何的参数,这些参数包括螺线的初始半径 a_{initial},螺线的最终半径 a_{final},以及期望的线圈匝数 n。于是可将螺线增长率 b 表示为:
我们还需要进一步确定螺线的起始角 theta_0 和终止角 theta_f。现在假设 theta_0=0、theta_f=2 \pi n,根据这些信息,我们便可以定义一组螺线几何参数。
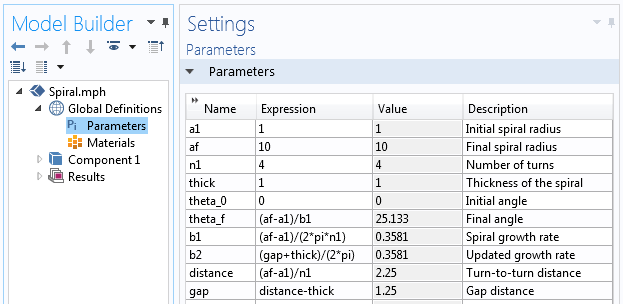
用于建立螺线几何结构的参数。
我们从三维分量 着手来建立螺线模型,首先在几何 分支中创建一个工作平面,随后在工作平面 几何中添加一条参数化曲线,并使用上文提到的角度可变的参数方程绘制一条二维阿基米德螺线。这些方程可直接输入到参数化曲线的表达式 编辑框中,或者我们也可以先在新的解析 函数中定义每个方程:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}
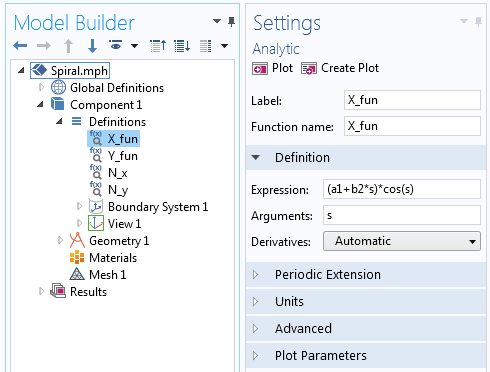
在 解析函数中对阿基米德螺线方程的 X 分量进行定义。
解析 函数可用在“参数化曲线”的表达式中。在“参数化曲线”中,我们将参数 s 的变化范围设置为由螺线的初始角 theta_0 开始,到螺线的终止角 theta_f=2 \pi n 结束。
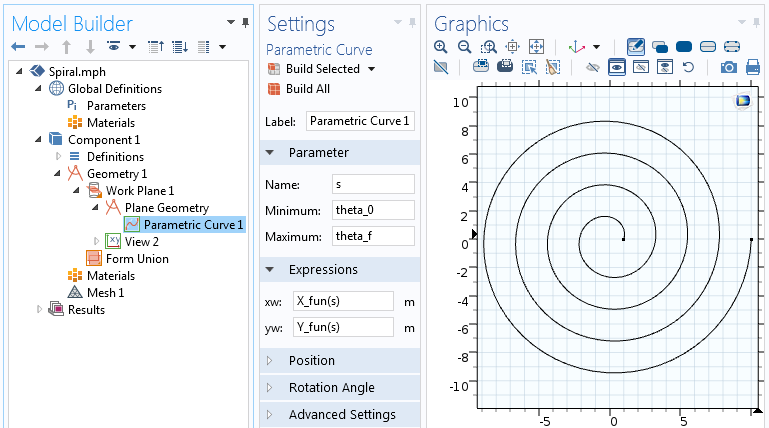
“参数化曲线”特征的设置。
在“参数化曲线”特征中使用的参数化螺线方程可将螺线以曲线方式呈现出来。现在,让我们以该几何结构为基础,为其添加厚度来创建一个二维实体对象。
到目前为止,螺线的初始半径 a_{initial}、最终半径 a_{final} 及期望的线圈匝数 n 已经实现参数化。现在,我们必须加入厚度,作为螺线方程的另一个控制参数。
让我们从螺线的主要属性开始着手,它规定螺线线圈之间的距离为 2 \pi b,也就是等于 \frac{a_{final}-a_{initial}}{n}。为了引入厚度,我们将螺线中相邻两匝线圈之间的距离表示为螺线厚度与线圈间剩余间隙之和,即 thick+gap。
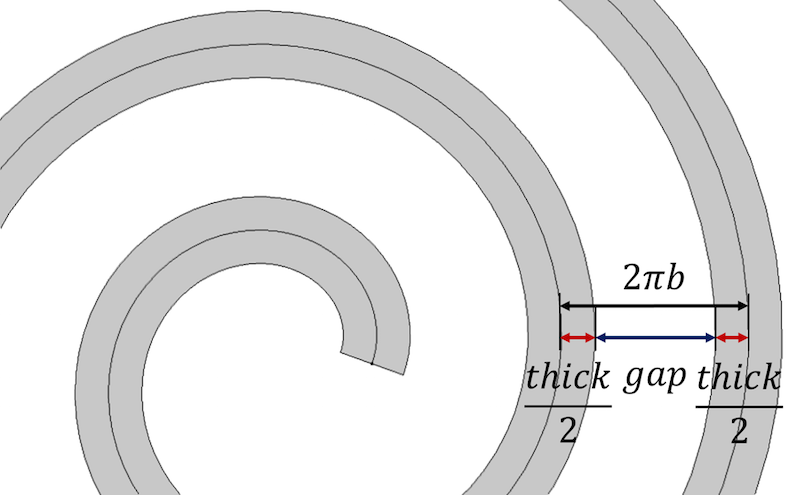
以螺线厚度和间隙参数的形式来定义螺线中相邻线圈之间的距离。
为了控制厚度并使相邻两匝线圈之间的距离相等,可将距离表示为:
distance=\frac{a_{initial}-a_{final}}{n} \\
gap=distance-thick
\end{align*}
定义完厚度,并将其和螺线中心线之间的恒定距离用于表示线圈之间的间隙后,现在可以利用厚度将螺线的增长参数重写为:
distance=2\pi b \\
b=\frac{gap+thick}{2\pi}
\end{align*}
我们还想将终止角以螺线的初始半径和最终半径的形式表示为:
\theta_{final}=2 \pi n \\
a_{final}=\text{total distance}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}
\end{align*}
您希望使螺线的起始角为非零值吗?如果是的话,则需要在最终角的参数表达式中添加初始角:theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0。
复制两次现有的螺旋曲线,并将这两个复制螺线分别置于与初始螺旋曲线偏移为 -\frac{thick}{2} 和 +\frac{thick}{2} 的地方,即可建立具有特定厚度的螺线模型。为了准确放置上下螺线,我们必须确保偏移螺线与初始螺旋曲线垂直。为了实现这一点,我们可以将偏移距离 \pm\frac{thick}{2} 与垂直于螺旋曲线的单位矢量相乘。曲线的法向矢量方程的参数形式如下:
其中,s 为“参数化曲线”特征中使用的参数。为了获得单位法向,我们需要用上述方程除以法线长度:
偏移量等于一半厚度的阿基米德螺线的参数方程更新后如下:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{component}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
\end{align*}
在参数化曲线表达式编辑框中填写以上方程非常耗时。因此,我们推荐您使用以下记数法:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
在这里,我们通过 COMSOL Multiphysics 中的解析 函数来定义每个 N_x 和 N_y,这与我们定义第一个参数化曲线中的 X_{fun} 和 Y_{fun} 的方式类似。在函数中,我们使用微分算子 d(f(x),x) 来求导,如下方截图所示。
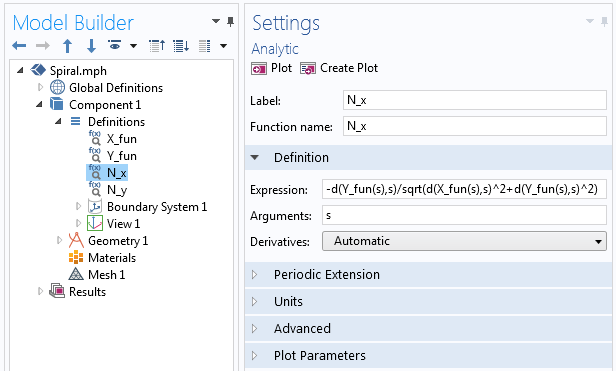
用在 解析函数中的导数算子示例。
函数 X_{fun}, Y_{fun},N_x 及 N_y 随后便可被直接用于在参数化曲线表达式中对其中一侧的曲线进行表示:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
该函数也能被用于表示另一侧的曲线:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
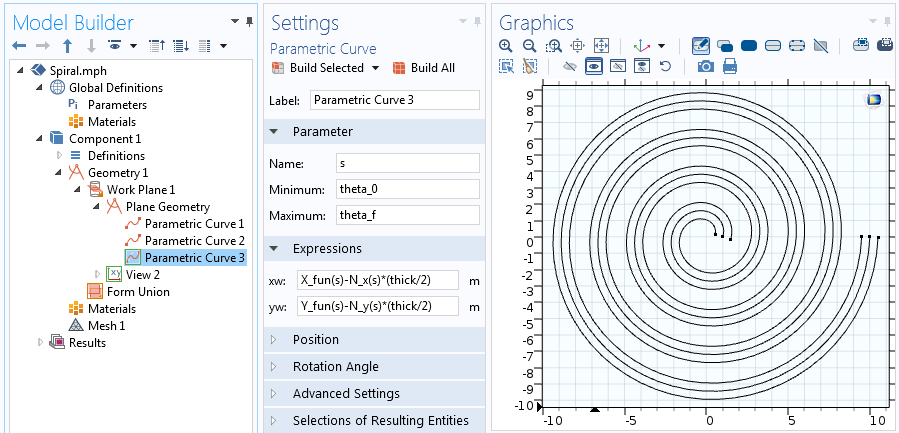
两条偏移参数化曲线中的第二条对应的方程。
为了连接两条曲线的端部,我们使用上文中略加修改后的方程添加了两条参数化曲线。对于连接螺线中心的曲线,我们必须计算 X_{fun}, Y_{fun},N_x 及 N_y 以获得角 theta 的起始值。对于连接螺线外侧的曲线,我们必须计算 theta 的最终值。因此,位于中心的连接曲线如下:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
同时,外侧的连接曲线为:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
在上述两个方程组中,s 的范围为 -1 至 1,如下方截图所示。
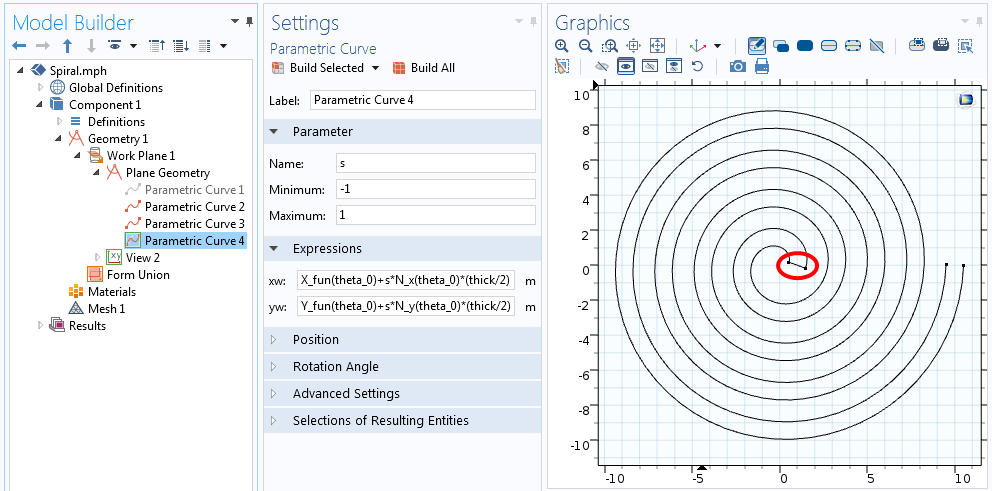
与螺线的一端相连的曲线的方程。
现在,我们已经有了五条用于定义螺线的中心线和四侧的轮廓的曲线。因为描述中心线的曲线并非必要元素,因此我们可以禁用(甚至删除)它,仅留下螺线轮廓即可。定义螺线的轮廓后,我们可以执行转换为实体 操作以创建单个几何对象。通过执行拉伸 操作,我们可以将二维螺线最终拉伸为三维。
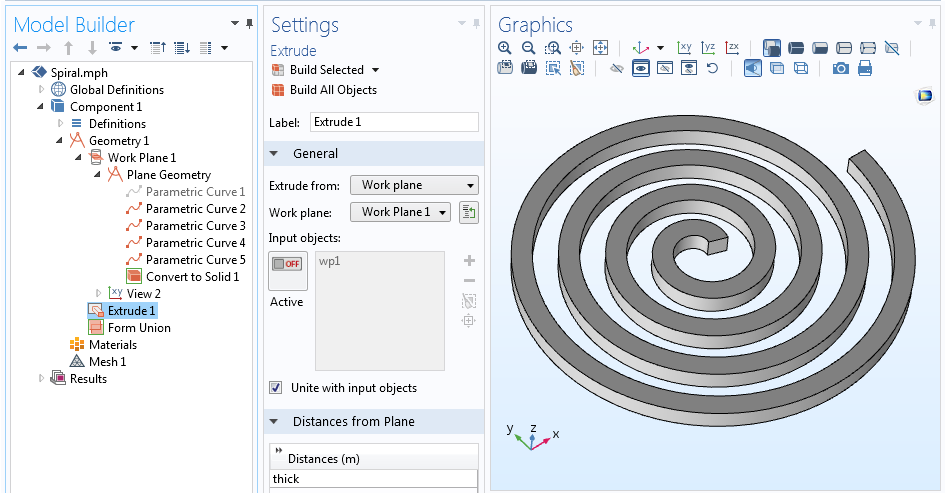
全几何序列和拉伸的三维螺线几何结构。
关于在 COMSOL Multiphysics 中模拟阿基米德螺线的结束语
我们已为您演示了全参数化阿基米德螺线的完整创建步骤。在这个螺线几何结构中,您可以修改所有参数,并对不同的设计进行实验,甚至还可将它们用作优化研究的参数。我们鼓励您在自己的建模过程中使用这一技术,进而帮助您分析以阿基米德螺线为基础的特殊工程设计。
更多关于螺线设计与分析的资源
- 为了进一步探究仿真在螺线模型设计中的应用,您可以参考以下教学模型:
- 阅读相关的用户成功案例:《螺旋谐振腔滤波器分析》





评论 (5)
锦 何
2018-09-11非常感谢你的分享 解决了困扰我的难题
Tengyue Gao
2018-10-12何锦,您好!
非常高兴能够帮助到您~
Chen Niu
2019-04-16nice
D 陈
2023-12-18请问参数化线可以增加分辨率吗?
没延 韩
2023-12-20 COMSOL 员工可以通过改变最大节数来增加曲线的光滑度