带标签的博客文章 技术内容

COMSOL Multiphysics® 中的高效参数控制和使用
2019年 6月 4日
任何模型都可以从适当的参数列表中受益。 了解如何通过参数节点和表单等功能更有效地控制和使用模型参数。

如何使用集总元件对机械系统建模
2019年 5月 29日
模拟一个大型、复杂的系统?您可能想要简化模型设置中的配置,以便更好地理解它,但是如何做呢? 进入 COMSOL Multiphysics 中的集总机械系统接口。
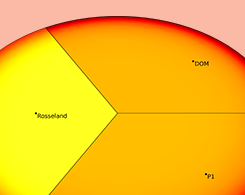
参与介质中辐射传热的 4 种计算方法
2019年 5月 22日
离散坐标法,P1 近似,Rosseland 近似,或者比尔-朗伯定律:你应该用哪一个来分析参与介质的传热?
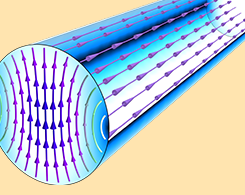
如何在 RF 模块中使用圆形端口
2019年 5月 10日
RF 模块中的 端口 边界条件是 COMSOL Multiphysics® 软件的附加功能,可用于发射和吸收电磁能。在本篇博客中,我们将介绍如何设置一个圆形波导端口,并检查定义端口模场的解析解。

参与介质中的辐射传热和离散坐标法
2019年 5月 8日
这里一份关于离散纵坐标法,正交集,以及如何模拟辐射和参与或吸收介质之间的相互作用的完整指南。
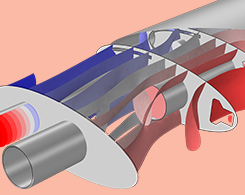
在声波导模型中使用端口边界条件
2019年 4月 25日
通过结合几个端口边界条件,可以很容易地计算在排气和消声器系统的传输和插入损失。阅读本文,了解在声学建模应用此特征的更多好处。

如何在数值上简化周期性射频模型
2019年 4月 22日
有时,射频应用中会出现周期性结构,例如频率选择表面(FSS)、电磁带隙(EBG)结构、响应阻抗表面(RIS)、高阻抗表面(HIS)和超材料。如果要解决仿真中的全部周期性问题,那将需要较高的计算成本和较长的计算时间。本篇博文,我们将通过 COMSOL 附加产品 —— 射频模型案例库中的几个示例,展示如何使用周期性边界条件简化复杂的数值模型。
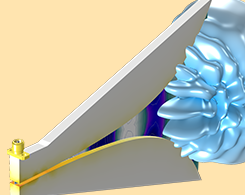
RF 模块中的物理场接口和研究指南
2019年 4月 19日
RF 模块包括 4 个物理场接口和研究,可以用于分析射频分析中的电磁波传播和共振行为。
