论文和技术资料

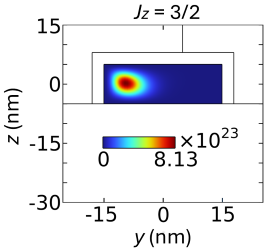
Among the various technological platforms, which are currently investigated as candidates for the implementation of large-scale multi-qubit quantum computers, spin qubits in silicon quantum dots (QDs) are one of the most attractive. Long spin lifetimes can indeed be achieved in isotopically purified silicon. Silicon is also a natural platform for the co-integration of quantum devices with classical electronics. On the modeling side, the availability of a Quantum-CAD (QCAD) framework would be highly desirable to assist device designers and explore new solutions, similar to well-established TCAD tools in nanoelectronics. We present a QCAD tool based on COMSOL Multiphysics for the simulation of hole spin qubits. It calculates the electrostatic potential profile and the energy levels of a hole in a quantum dot, in the presence of a static magnetic field. This computation is performed in a self-consistent way, by solving the coupled Poisson and Schrӧdinger equations. The gyromagnetic matrix g and its derivative g’ with respect to the gate voltage are also calculated from the wavefunctions at zero magnetic field [1]. The matrices g and g’ allow for the computation of the Rabi frequency as a function of the magnetic field to first order in the magnetic field and in the gate voltage. Results for a qubit hosted in a silicon nanowire fabricated in SOI technology (shown in Fig. 1) are presented. The potential profile in the device is first computed with a finite volume Poisson solver. The wavefunctions are then calculated with a four-bands k∙p Luttinger-Kohn (LK) Hamiltonian for the valence band (Fig. 2). Essentially this model accounts for heavy-hole (HH) and light-hole (LH) bands. The Hamiltonian matrix is discretized on a finite difference mesh. The benchmark models k·p Method for Strained Wurtzite GaN Band Structure and A Silicon Quantum Dot in a Uniform Magnetic Field from the Application Libraries show how to set up multiple wavefunction components with the Schrödinger Equation interface. LiveLink™ for MATLAB® allows to easily control the iterative procedure for Poisson-Schrӧdinger solution. The squared HH and LH envelopes of the ground state are plotted in Fig. 3. The dominant HH character of the ground state is evident. The g and g’ matrix elements are computed as integrals involving the zero-field states of the qubit, as demonstrated in [1]; these terms are efficiently calculated by COMSOL. Finally, from the knowledge of g and g’, Rabi frequency is computed as a function of the magnetic field (Fig. 4). In conclusion the presented framework allows for the numerical characterization of hole spin qubits. It can be used as a basis tool for the calculation of more advanced qubit characteristics such as the sensitivities to geometrical parameters, material defects and process variations. Results have been presented for silicon, but the tool can handle other types of semiconductors, e.g. Ge/SiGe.