Terminology and Requirements for Swept Meshing
In the first part of this course, we learned the circumstances in which a swept mesh can be useful. In Part 2, we dig into the details of a Swept operation: the terminology used for it and when exactly it can be used.
Terminology of a Swept Mesh
Let's begin by presenting some terminology used in COMSOL Multiphysics® regarding swept meshing. Each face about a domain that is to be operated on by the swept mesher is classified as either a source face, a destination face, or a linking face. The Swept operation starts from the source faces and terminates at the destination faces, hence defining a sweep direction. The linking faces connect the source and destination faces.
The linking edges are the edges, or the chains of edges, that are approximately tangent to the sweep direction. The section edges are the edges, or chains of edges, that are approximately perpendicular to the sweep direction.
A section is a face component bounded by two loops of section edges.
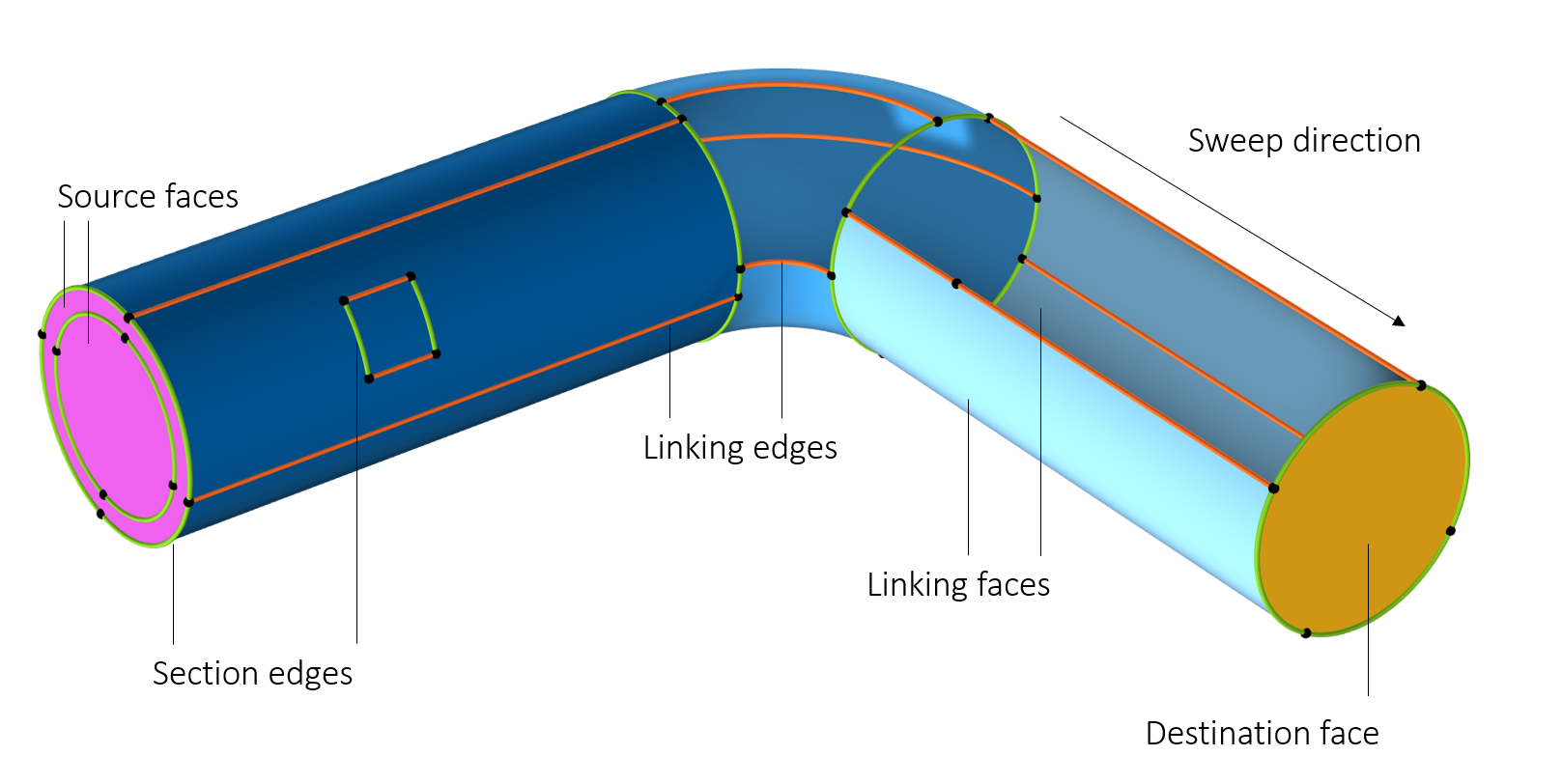 Classification of the boundaries and edges about a domain used for swept meshing. The sections are depicted by the three shades of blue. Two faces are hidden to show the inside of the domain.
Classification of the boundaries and edges about a domain used for swept meshing. The sections are depicted by the three shades of blue. Two faces are hidden to show the inside of the domain.
Requirements for a Swept Mesh
The very first step before even trying to generate a swept mesh is to ensure that the domains are following several criteria, as described in the documentation. Since each domain within the geometry selection that will be swept follows the same logic, we will focus on one domain in this part. The different criteria from the documentation can be loosely summarized with four major rules:
- No holes, isolated faces or voids in the domain
- The source and destination must be connected face components
- Each destination face matches one or more source faces, while each source face matches exactly one destination face or its subset
- For each section, there must be at least two chains of linking edges
We will explore each of these requirements in detail as some technicalities were eluded deliberately in this list. If any of these requirements are not met, an error message will appear. Techniques on how to solve these and any other potential issues are covered in the next part of this swept meshing course.
Requirements on the Shape of the Domain
Handling of Holes, Isolated Faces and Voids
No holes, isolated faces or voids are allowed in the domain. The only exception to this rule is if the holes or isolated faces penetrate both source and destination, as shown in the next picture.
How the Source and Destination Are Connected to the Domain
The source and destination must be connected face components.
Another way to interpret this rule on a domain level is to say that the domain cannot "branch off", it cannot start or end at different disconnected locations.
On a side note, this rule does not mean that the source and destination must be be forming different connected face components, coincident source and destination faces are also supported. These are allowed as long as the source mesh matches the destination (i.e., including the potential twist of the face).
Visualizing the Sweep Path
It is often helpful to mentally visualize the sweep by following the cross section of the mesh. An interpretation of the first two rules is that the cross section must not have any abrupt changes in its shape. For example, a hole will create a void in the cross section, an isolated face will introduce a new edge edge, and a branching will either split, combine, add, or remove faces in the cross section. While this technique is not the most rigorous, 'cross section' and 'abrupt change' need to be properly defined, it will in most cases help to locate where a domain becomes unsweepable and will give a clue where it might help to partition the domain.
A way to help with this visualization is to add a Clip Plane that is parallel to the cross section of the sweep, and then drag the frame of the clip plane in the sweep direction. Make sure to select the option Show Cross Section.
The Special Case of Isolated Entities
Isolated edges and isolated vertices are edges and vertices that are positioned inside a domain or face without being part of any loop of edges delimiting a face. When isolated edges and vertices are present, the mesh is first generated without considering isolated entities. Then, in the second step, the entities are included and essentially "glued" to the existing mesh by moving some nearby mesh nodes. The mesh conforms to the isolated entities during the sweep.
 The exterior of a mesh with and without isolated entities on the linking faces.
Visualization of the mesh, without (left) or with (right) isolated entities located on the linking faces. The mesh on the right has been distorted in order to account for the additional entities during the sweep. Note that the total number of mesh elements remains constant because the isolated entities are snapped afterward; this means that they need to be placed reasonably so that the mesh is not distorted excessively.
The exterior of a mesh with and without isolated entities on the linking faces.
Visualization of the mesh, without (left) or with (right) isolated entities located on the linking faces. The mesh on the right has been distorted in order to account for the additional entities during the sweep. Note that the total number of mesh elements remains constant because the isolated entities are snapped afterward; this means that they need to be placed reasonably so that the mesh is not distorted excessively.
 The interior of a mesh with and without isolated entities on the linking faces.
Visualization of the interior mesh, without (left) or with (right) isolated entities located within the domain. The mesh on the right has been distorted in order to account for the additional entities during the sweep.
The interior of a mesh with and without isolated entities on the linking faces.
Visualization of the interior mesh, without (left) or with (right) isolated entities located within the domain. The mesh on the right has been distorted in order to account for the additional entities during the sweep.
Source and Destination Faces Requirements
Each destination face matches one or more source faces, while each source face matches exactly one destination face or its subset. In other words, the source faces can contain more faces than the destination, as long as there is a way of imprinting the mesh onto the destination (up to some distortion, like we saw in this animation)
This geometry can be swept meshed even though there are more source faces (magenta) than destination faces (yellow).
For the majority of cases there is no deformation between the source and destination, one can simply translate and rotate the source faces to overlap on top of the destination faces. In that case, it can help to mentally visualize copying the source mesh to the destination, and see if the copy operation is possible. This mental exercise is depicted in the next animations.
Note that destination faces cannot contain any isolated edges, even if it would match perfectly isolated edges on the source faces. For isolated vertices on the destination faces (and their boundaries), they will be handled the same way as described in this section: the mesh will be locally distorted in order to snap those vertices to mesh nodes. For the source faces, they can both contain isolated edges and vertices.
Linking Edges Requirements
For each section, there must be at least two chains of linking edges. Another way to interpret this rule is that there should at least be two linking faces per section.
Concluding Remarks
In this article we discussed how to distinguish domains that can or cannot be meshed with a swept mesh and four simple rules to check for. To see how the swept mesh was generated for several of the model examples included in this article, you can see the respective MPH-files attached. In the next part of the swept mesh course, we present the most important aspects to take into account so that a mesh of good quality can be generated.
请提交与此页面相关的反馈,或点击此处联系技术支持。
