论文和技术资料

Relative permeability maps for steady-state two-phase flow in porous media, delivered by implementing the DeProF model [1] algorithm, were integrated within COMSOL Multiphysics® software [2] to resolve field-scale flows in porous media.

The mechanistic model DeProF [1], predicts the relative permeability of oil and water in terms of the capillary number, Ca, the oil/water flowrate ratio, r, the oil/water viscosity ratio, M, the advancing and receding contact angles, and a parameter vector, comprising the dimensionless geometrical and topological parameters affecting the flow. The DeProF model is the first mechanistic model describing the flow in terms of its actual independent variables, Ca, and r. It shows improved performance over the conventional modeling of saturation-described flow. Not only the DeProF model matches the process phenomenology with a remarkable specificity, but it also reveals latent phenomenology, e.g. the existence of optimum operating conditions. The latter has been recently confirmed by a major re-examination of laboratory studies [3] and is justified on the basis of statistical thermodynamics principles [4]. In that context, the DeProF theory provides a deeper and more accurate (true-to-mechanism) description of the sought process and the underlying mechanisms.

Extended simulations with the DeProF model algorithm in a 3D pore network of the chamber-and-throat type, delivered macroscopic, reduced pressure gradient maps, x, expressed in the form of a scaling law function of Ca & r, x(Ca,r) [1], Figure 1. Such map was integrated into the COMSOL model.

A lean integration scheme capable of handling steady-state two-phase flow problems was developed. The model treats the two-phase flow problem as an equivalent one-phase flow problem of a virtual fluid having a local effective mobility equal to the sum of the local mobilities of oil and water. The algorithm solves the equivalent 1-ph flow problem combining Darcy’s law with the continuity equation and the transport equation for the apparent fluid density and viscosity, calculated as saturation-weighted averages of oil/water properties, while considering dependence of the effective hydraulic conductivity on local flow conditions. The latter are described by the total flowrate intensity (effective superficial velocity), equal to the sum of oil and water velocities.

For a local set of oil and water velocities, the local values of Ca & r are readily computed and the local effective mobility is estimated as the sum of the local oil & water mobilities. These, and the reduced pressure gradient, are looked-up from the DeProF map for the corresponding Ca, r values. Implementation of the standard Darcy velocity vs pressure gradient relation for the equivalent phase, delivers the new effective superficial velocity. This latter is decomposed into a set of local oil & water superficial velocities according to the value of the flowrate ratio. The procedure is repeated along the effective flow streamlines which coincide with the actual 2-ph flow streamlines.

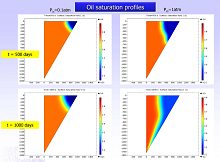
The integration scheme has been applied to a variety of injection/production patterns, solitary wells, 7-spot well arrangements [5,6], Fig. 2, and for different orientations, including gravity effects, Fig.3.