Modeling History Dependent Heating of Viscoelastic Polymers under Harmonic Excitation
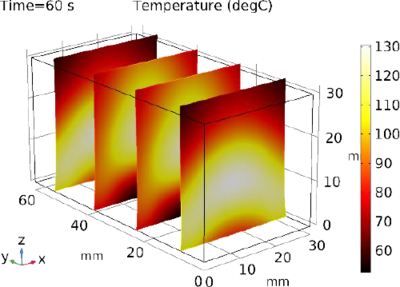
Soft lossy viscoelastic polymers can dissipate significant amounts of energy in the form of heat when subjected to dynamic mechanical stimuli. As a result, structures comprised of such lossy materials may heat up considerably when excited by loads at a frequency that approaches one of the structure’s natural frequencies. For example, a lossy viscoelastic solid tends to heat up significantly more when exposed to a loading history in which the excitation frequency ramps down, as opposed to a loading history in which the excitation frequency ramps up within the same bounds. This peculiar phenomenon can compromise the integrity of heat sensitive structures but could also be a desired system property. When the time scale of heating is much longer than that of the mechanical excitation that provides another source of complexity, that is best treated with a time dependent thermal analysis coupled to a harmonic vibration analysis. This capability is not hard coded in most commercial finite element codes. In this study we develop such models in COMSOL Multiphysics® to study the nonlinearities of the mechanically induced heating of lossy viscoelastic solids. Our models make use of the coupled thermal-mechanical analysis provided by COMSOL Multiphysics® in which a solid is harmonically excited with harmonic loading with a frequency that slowly changes with time. The excitation frequency is close to the first natural frequency of the structure. The solid is heated by volumetric heat sources providing the energy dissipated due to the viscous nature of the solid. Figures 1 and 2 show the predictions of our COMSOL® model in the case of a rectangular viscoelastic block. In Figure 1 we report the average temperature in the block during the frequency ramp-up step (blue curve) and during the frequency ramp-down step (black curve). Figure 2 shows temperature slices of the viscoelastic rectangular block at the end of the frequency ramp down step.
下载
- N_Vasios-COMSOL Conf 2020.pdf - 1.96MB
