论文和技术资料

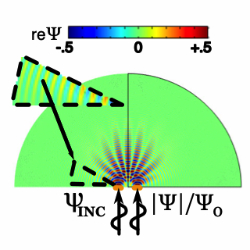
INTRODUCTION: The “Schrödinger equation” is usually associated with quantum mechanics, however for the nonlinear version (NLSE), there are applications outside the realm of quantum mechanics. NLSE appears in branches of physics like a) the quantum physics Bose-Einstein condensation (BEC), b) water wave analysis via the Davey-Stewartson system (subject of 2025 COMSOL Conference paper), d) plasma and particle physics, e) semiconductor applications, f) first principle material simulation, g) superfluids, and h) biological molecular systems. COMSOL is used herein for obtaining the BEC quantum mechanics wavefunction Ψ(x,y,z,t) as a solution to the time dependent nonlinear Schrödinger equation (NLSE) representing a typical (near absolute zero) boson particle while it interacts with N like neighboring particles. The additional nonlinear term [1] in the linear Schrödinger equation is caused by interactions with the contiguous boson particles. The probability density evaluation of a particle being at a spatial point can be obtained from |Ψ|^2. Numerical solutions to NLSE are sought herein and because it involves solving field PDEs, COMSOL is directly adaptable to this type problem. USE OF COMSOL MULTIPHYSICS: Nonstandard PDE’s often encountered in physics research is a good fit for applying COMSOL’s general equation solving capabilities. The Equation Based Modeling General-Form PDE "time dependent" study is employed herein. The distortion of the freely propagating Schrödinger equation plane waves by the presence of a V(x,y) potential and/or a nonlinear βΨ|Ψ|^2 term in the linear Schrödinger equation is examined through a series of examples by varying the V, β parameters. A local k-ω dispersion relation ( temporarily holding {x,y} constant in the spatial PDE coefficients over a small spatial neighborhood) provides a-priori information about the required spatial FEM mesh size. RESULTS: A series of increasing complex models are examined starting with the Fig.1 simple Free Field PW propagating down a wave guide, and then encountering a nonlinear region (with potential V(x) < 0 ) starting at x=18 ; Fig.2 is same as 1) except V(x) > 0. With the same model parameters employed in the 1D examples, 2D models are examined by passing incident waves through 1 slit as in Fig.3 and then through 2 slits as in Fig.4 . The build up of constructive and destructive interference patterns are tracked as the wave engages with the nonlinear field. In these Figs. 1-4 examples, the effect of varying controlling model parameters such as the potential field, nonlinear PDE coefficient, and temporal drivers (steady wave train vs short pulse ) are evaluated . CONCLUSION: The application of COMSOL to pure physics is explored and successfully applied, with particular emphasis on solving nonlinear partial differential equations. Validation checking against alternative FEM solutions showed good comparisons. The examples illustrate the value of COMSOL in studying the effects of the nonlinear strength multiplier β and potential V on the interactions physics. The local k-ω dispersion relation is a useful relation for a-priori determining regions of wave propagation.