问题描述
在求解瞬态模型时,需要考虑各物理量随时间的变化。为此,软件会基于给定的初始条件,使用一种时间积分算法来计算未知变量会如何随时间变化。在计算过程中,有时收敛较慢,有时不完全收敛。本文针对如何解决这种情况提供相关指导。
解决方法
背景
COMSOL Multiphysics 瞬态(时间相关)求解器能够求解以下形式的方程组:
其中,
和
可以是常数,或者是
和
的非线性函数。这些方程既可以是独立的常微分方程 (ODE),也可以是耦合方程组,它们是通过有限元法 (FEM) 对边界值问题 (BVP) 进行空间离散化产生的。您在 COMSOL 中求解的大多数时变场和空间变化场问题都属于后一类。结合上述方程,软件可以求解一般形式的代数方程组:
,这两组方程形成微分代数方程 (DAE)。这个微分代数方程加上一组初始条件
,就可以完全定义瞬态模型。另请注意,软件还可以处理具有更高阶时间导数的模型,只需引入额外的中间变量即可。
时间步进法
COMSOL 提供三种方法用于求解微分代数方程:向后差分公式法、广义 α 法和龙格-库塔法。向后差分公式法和广义 α 法是隐式方法,龙格-库塔法是显式方法。显式方法根据当前状态下的解直接计算未来状态下的解。隐式方法根据未来状态和当前状态下的解形成一个方程组并进行求解。隐式方法通常比显式方法更稳定、快速,但显式方法使用的内存更少。软件将根据所用的物理场接口自动确定最合适的方法,一般不建议替代默认的求解器方法。
要查看所使用的求解器,您可以在求解器配置的瞬态求解器节点中查看时间步进设置,如下面的屏幕截图所示。

查看所用求解器方法的位置。
龙格-库塔法主要用于求解常微分方程组以及涉及时域显式压力声学 和时域显式电磁波 物理场接口的模型。因此,这种方法的使用范围非常狭窄,不在本知识库文章的讨论范围内。
对于已确定解本质上是振荡的(类似波)模型,例如声学模型、电磁波模型以及包含惯性项的结构瞬态模型,通常默认使用广义 α 法。这些类型的问题最好通过指定单元大小和求解器时步来求解。有关如何设置网格和选择时间步长的指导信息,请参见关于解析瞬态波的文章,还可参见知识库 1244:求解载荷呈阶跃变化的波型问题。遵循上述准则应该可以解决此类模型的大多数收敛问题。
对于涉及扩散、对流和反应的有限元模型,通常默认使用向后差分公式法,这些情况代表了受益于求解器设置调整的大多数情况。系统使用自适应或自由时间步进方案求解这类问题,求解器将自动调整时间步长。这些情况正是本知识库文章讨论的重点。
需要注意的是,默认情况下,求解器按请求的时间步长(而不是求解器实际采用的时间步长)返回解。有关这方面的更多详细信息,以及如何替代此特征,请参见知识库 1254:控制瞬态求解器的时间步长。
调整瞬态求解器
对于默认使用向后差分公式法和自由时间步进求解的扩散、对流和反应问题,需要注意以下几点。以下各方面相互结合,将影响求解器的收敛性。
使用事件接口模拟步长变化
如果模型中的载荷或边界条件将随时间发生瞬时变化(在已知时间或已知条件下),则应通过引入事件接口来求解此类问题。请参见:求解包含时变脉冲载荷的模型。“事件”接口可确保求解器准确捕获载荷的所有阶跃变化。
求解器相对容差
在使用自适应时间步进(使用任意求解器方法)时,软件会自动调整所用的时间步长,以满足所需的相对容差。尽管在这种情况下,精确选择时间步长相当复杂,并且无法直接控制,但您可以控制相对容差,如下面的屏幕截图所示。您应该总是执行容差细化研究:用更严格的容差重新求解模型并比较结果。

用户控制的相对容差设置。
相对容差与瞬时误差和随时间累积的误差都相关。由于误差会累积并增大,因此,过于宽松的相对容差会产生误差主导的解,如果您发现求解器最初采用相对较大的时步,随后采用相对较小的时步,可能就是这个原因造成的。用更严格的相对容差重新求解将导致求解器最初采用较小的时步,但累积误差会更小,因此在后续时步中,求解器可能不需要减小时步来克服累积误差。也就是说,相对容差越小,总体收敛速度越快。
网格
网格必须足够细化才能解析建模域中解场的变化。特别是对于涉及扩散、对流和反应的问题,不可能提前知道场中具有显著空间变化的具体位置。如果网格过于粗化,求解器可能需要采用非常小的时步来减小误差。因此,细化网格会导致求解器采用较大的时步,但代价是模型更大。请务必执行网格细化研究,如知识库 1261:执行网格细化研究中所述。
网格细化和相对容差细化是相辅相成的。您可以执行这两种研究,在相对容差与网格细化研究之间来回交替。
一致初始化
您可以建立边界条件与初始值不一致的模型。在使用一致初始化(默认情况下处于启用状态)时,仍然可以求解此类模型。但是,这可能不会完全达到预期效果,并可能在仿真开始时导致非常小的时步。有关更多详细信息以及如何解决此问题的指导信息,请参见知识库 1172:求解初始值不一致的瞬态模型。
缩放
由于数值原因,软件总是对要求解的未知数进行缩放。此操作是自动进行的,如果缩放得当,就不会有问题。但是,如果缩放比例不合适,则需要对场进行手动缩放。要了解如何检查和手动调整变量缩放比例,请参见知识库 1240:手动设置变量的缩放比例。
非线性求解器设置
在求解包含重要非线性项的模型时,求解器可能无法使用默认设置计算隐式方程组的解。要了解如何诊断和解决这类问题,请参见知识库 1127:提高非线性瞬态模型的收敛性。
初始时步
当求解器启动时,它会根据总仿真时间来估计要采用的初始时间步长。因此,如果您对同一模型求解两次,并且其总时间不同,则初始时步可能不同。如果在开始求解后立即发生了一些重大事件,这可能会导致不同的结果。要指定初始时间步长,请转到瞬态求解器设置,在时间步进栏中启用初始步长:选项,并输入固定的初始步长大小,如下面的屏幕截图所示。请注意,软件仍然可以自由选择小于该值的时步,但不会使其变大。此外,您还可以酌情考虑是否可以改用事件。
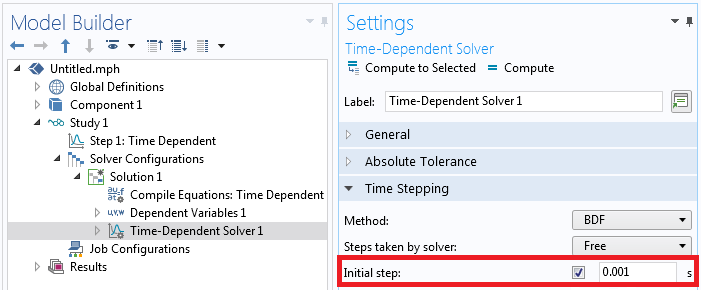 指定求解器尝试采用的初始时间步长。
指定求解器尝试采用的初始时间步长。
分离方法 vs. 全耦合方法
在求解多物理场模型时,软件的默认行为通常是以分离的方式来处理问题,先求解第一个物理场,然后求解下一个,并在每个时步中迭代所有物理场。这可能会严重影响收敛,具体取决于问题的性质。如果模型是用“分离”方法求解的,请尝试使用“全耦合”方法,反之亦然。在通过“全耦合”方法求解模型时,可能需要使用“直接”线性方程组求解器。要了解这些方法以及线性方程组求解器之间的区别,请参见知识库 1258:理解“全耦合”与“分离”求解方法,及直接与迭代线性求解器之间的区别。
处理非收敛模型
如果瞬态求解器无法收敛,它要么在初始条件下立即求解失败,要么在整个仿真过程的某个时间点失败。
如果是在仿真过程中的某个时间点失败,可以使用上述所有技巧来提高收敛性。此外,输出求解器得到的结果,如知识库 1254:控制瞬态求解器的时间步长中所述。绘制求解器失败时的时步的解以及该时步的前一时步的解,并观察这些解。使用“探针”来监控一些相关的量也很有帮助,如知识库 1255:减少存储在模型中的解数据量中所述。如果网格不够细化或者存在一些正在传播的累积误差,则绘制结果会特别突出显示。
如果求解器立即求解失败,首先需要仔细检查每个物理场接口中指定的初始条件,以及模型中各物理场的所有边界条件、载荷和约束。如果这些因素不一致,可能会导致求解器失效。默认情况下,求解器将试图通过找到与所有边界条件都一致的初始条件来更正这一问题,但这可能与预期有很大的不同。这种情况在涉及流动的模型中尤其常见,如知识库 1172:求解初始值不一致的瞬态模型中所述。
如果此操作符合您的实际情况,还建议您尝试建立一个等效或几乎等效的稳态(时不变)模型,此模型可以作为一个很好的测试平台,用于研究网格细化和缩放,以及比较分离方法与全耦合方法。有关处理非线性稳态模型的信息,请参见知识库 103:提高非线性稳态模型的收敛性。
COMSOL 尽一切合理的努力验证您在此页面上查看的信息。本页面提供的资源和文档仅供参考,COMSOL 对其有效性不作任何明示或暗示的声明。COMSOL 对所披露数据的准确性不承担任何法律责任。本文档中引用的任何商标均为其各自所有者的财产。有关完整的商标详细信息,请参阅产品手册。



