Computing Space and Time Integrals
In COMSOL Multiphysics®, you can evaluate integrals in both space and time in several different ways, either purely for results evaluation or to introduce feedback into your model. This article covers all of these options. Learn how to compute integrals over space or time and use the result of these integrals elsewhere in your model.
Spatial Integrals
The most general approach to taking integrals is to add a component coupling, Integration, to the Definitions branch of the model tree. This feature adds an operator name (intop1) that acts as a function and can be called anywhere else within the model. It can be used to define multiple different variables, as shown in the screenshots below. Note that integrating 1 over a domain is equivalent to evaluating the volume of that domain, integrating 1 over a boundary gives the surface area, and integrating 1 along an edge gives the length. If you add a component coupling after you have already computed the solution, you must click the Update Solution button in the Study node before the operator name will be available for results evaluation.
If you only want to integrate a single quantity, then using the Probe feature may be preferred to using a component coupling. The setup is slightly different and the results of a probe will automatically be plotted. Each probe defines a unique variable name that can be used anywhere else in the model. For time-dependent models, probes will be plotted at all time steps taken by the solver, by default.
If you do not want to use the results of the integral within your model, and you only want to evaluate integrals for results evaluation, then go to the Derived Values node and add an Integration feature, as shown below.
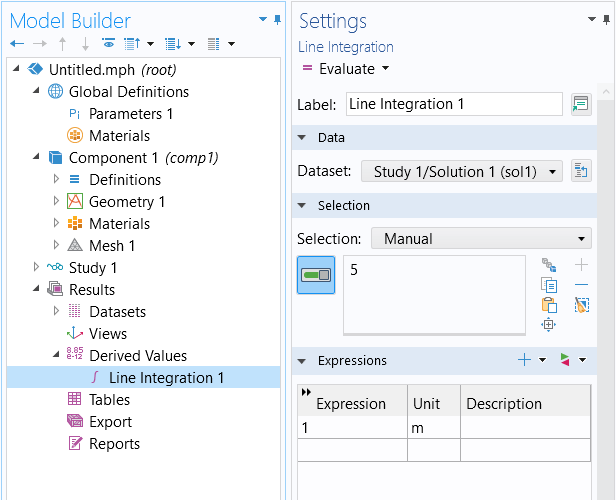
Taking an integral via the Derived Values node under the Results node.
Time Integrals
For most Derived Value nodes, in the Settings window, you will find you have the option to control the integration settings. The Integration option enables you to integrate the result over time, for a time-dependent solution, or over a parameter, for a parametric solution. Additionally, the Summation option lets you sum the results for each time step or parameter value.
 A screenshot of the Model Builder; Point Evaluation Settings window with the Data, Selection, Expression, Summation, and Data Series Operation sections expanded; and the Graphics window with a gray circle that has 4 blue points.
A screenshot of the Model Builder; Point Evaluation Settings window with the Data, Selection, Expression, Summation, and Data Series Operation sections expanded; and the Graphics window with a gray circle that has 4 blue points.The integration and summation options available in the Settings window for most Derived Value nodes, available to choose from through the Method drop-down menu.
You can also use the timeint operator in any results evaluation. For example, you can evaluate: timeint(1,2,T) to evaluate the integral of the expression T from 1-2 seconds. You can call integration operators within the timeint operator as well. See the Built-in Operators section of the COMSOL Multiphysics Reference Manual for additional documentation on the timeint operator.
If, on the other hand, you want to make the results of a time integration available within a model, add a Domain, Boundary, Edge, or Point, or the Global ODEs and DAEs interface. For example, suppose that you have defined the normalized Gaussian function via a Global Variable:
G = exp(-((t-0.5[s])/(0.1[s]*sqrt(2)))^2)/(0.1[s]*sqrt(2*pi))
If you want to take the time integral of this variable, then you can do so via the Global ODES and DAEs interface, as shown in the screenshot below. Define the name of a variable, TimeInt, that will store the time integral. Define the equation as d(TimeInt,t)-G, meaning that the time derivative of TimeInt equals G. You will want to adjust the units of the dependent variable and the source term as appropriate for the quantities you are integrating. This equation is solved from the initial value TimeInt=0 and thus it computes the integral, from t=0 to the current time, of the expression G. Note that you can take a time integral of the results of a spatial integral, meaning that the expression G could be replaced with an integration operator, for example.
 A screenshot of the Global Equation Settings window, with the Global Equations and Units sections expanded.
Taking a time integral via a global equation.
A screenshot of the Global Equation Settings window, with the Global Equations and Units sections expanded.
Taking a time integral via a global equation.
Further Learning
For more information on performing space and time integrals in COMSOL Multiphysics®, we refer you to our blog post providing an overview of integration methods in space and time, which uses a 2D heat transfer problem to demonstrate. Included at the end of the blog post are several links connecting you to various model examples that utilize space and time integrals, all of which are available in the Application Libraries.
请提交与此页面相关的反馈,或点击此处联系技术支持。
