“案例下载”页面提供丰富的 COMSOL Multiphysics® 教学案例和 App 演示文件,涉及电气、结构、声学、流体、传热和化工等各个学科领域。欢迎下载这些教学案例或 App 演示文件及其随附的操作说明,将其作为您建模仿真工作的绝佳起点。
您可以使用左侧的【快速搜索】工具查找与您的专业领域相关的案例模型和仿真 App。请注意,此处提供的许多案例也可以通过 COMSOL Multiphysics® 软件内置的“案例库”进行访问,该选项位于软件的文件 菜单中。
中文 带有此标签的案例包含中文 PDF 文档。
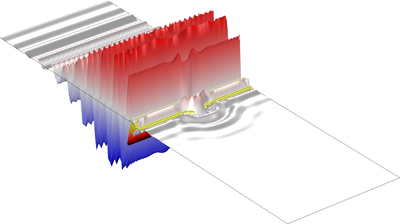
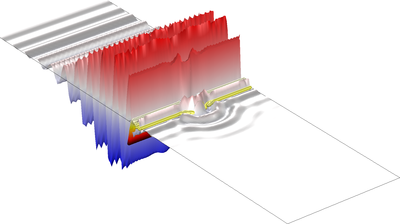
本教学案例演示如何求解等离子体和半导体等色散介质中的全瞬态波动方程。二维 TM 面内波模型根据波动方程求解矢势,并根据常微分方程求解辅助电极化密度。 几何结构由一块具有亚波长狭缝的色散板组成,其中应用周期性边界条件 ... 扩展阅读
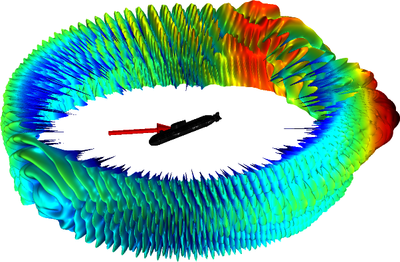
扬声器悬架的作用是将膜保持在适当的位置,从而避免音圈产生摇摆运动。在低频时,膜的位移非常明显,悬架的刚度随着音圈的运动而变化,这种变化(或非线性)是扬声器中产生的总失真的重要来源 ... 扩展阅读
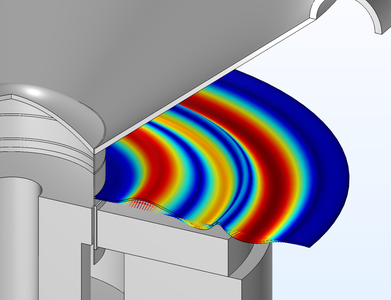
在移动设备、消费电子产品、助听器或耳机的开发过程中运行仿真时,我们需要考虑换能器如何与系统的其余部分相互作用。本例中,我们介绍如何使用换能器的集总表示来分析隔振装置与微型助听器换能器(Knowles® TEC ... 扩展阅读
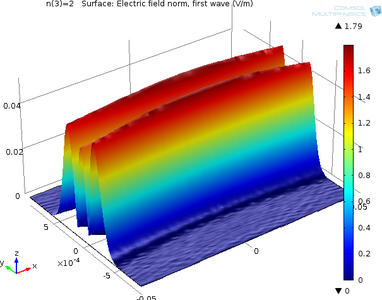
此模型演示如何建立非线性方程组来求解对称激光腔的特征频率,其中使用“电磁波,波束包络”物理场接口的双向公式。 计算得出的特征频率通过解析式的值进行验证。 扩展阅读
本教学案例演示如何求解等离子体和半导体等色散介质中的全瞬态波动方程。二维 TM 面内波模型根据波动方程求解矢势,并根据常微分方程求解辅助电极化密度。 几何结构由一块具有亚波长狭缝的色散板组成,其中应用周期性边界条件 ... 扩展阅读
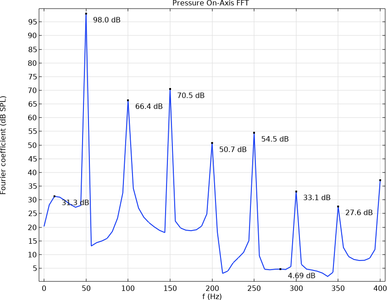
此教学案例演示如何计算电容耦合等离子体的阻抗。通过时间周期 研究计算等离子体的时间周期解,随后,将解转换为时域解,再调用快速傅里叶变换 (FFT) 求解器,这样可以针对给定的一组输入参数计算等离子体阻抗 ... 扩展阅读
本模型演示如何在简化的扬声器分析中包含某些集总元件的非线性(大信号)特性,并使用等效电路对机械和电气系统进行建模,其中的大信号柔度 CMS(x) 和力因子 BL(x) 是扬声器位置的非线性函数。此外,机械阻尼 RMS ... 扩展阅读
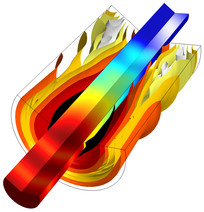
此模型在子模型中利用热黏性声学接口获得穿孔板转移阻抗的详细结果(包括热损耗和黏滞损耗)。 阻抗又用作消声器的压力声学模型中的内部阻抗。将结果与经典阻抗模型和测量结果进行了比较。 扩展阅读
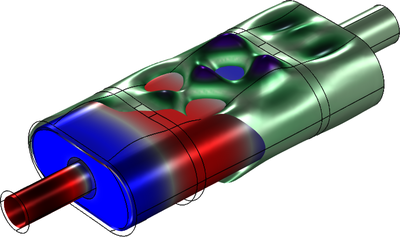
此模型描述内燃机消声器中压力波的传播,模型的目的是介绍如何分析压力声学中的电感和电阻阻尼,以及如何将流体耦合到消声器的周围弹性壳结构。最后,分析纯结构问题的特征模态,并将模态与传输损耗峰值进行比较。 扩展阅读