论文和技术资料

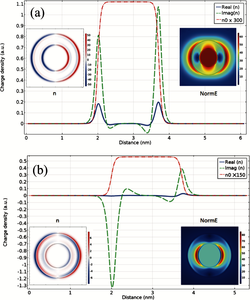
Quantum Hydrodynamic Theory (QHT) provides an excellent method to study both near-field and far-field properties of multiscale plasmonic systems, especially for systems whose sizes make it computationally prohibitive for the density functional theory approach [1]. The microscopic behavior of these structures significantly differs from the classical predictions due to nonlocal or quantum effects. QHT can accurately and efficiently describe both the plasmon resonances and the spill-out effects of microscopic as well as macroscopic plasmonic structures by including the nonlocal contributions of the kinetic energy and correct asymptotic description of the electron density. The hydrodynamic equation of motion of an electronic system when coupled to the Maxwell equations leads to the following set of equations: ∇×∇×E − ω²/c²E=ω²μₒP 1(a) cnₒ/me ∇(δG/δn)+(ω²+iγω)P=−εₒωp²E 1(b) where the variables represent the usual quantities. The energy functional G[n] can be written as the sum of Thomas-Fermi kinetic energy T₁, von Weizsäcker kinetic energy T₂ and exchange-correlation potential energy E of the electronic system, as: G[n] = T₁[n] + T₂[n, ∇n] + E[n] (2) The terms appearing in the above equation are nonlinear function of charge density n and its gradient ∇n and are explicitly expressed in [1]. We have used COMSOL Multiphysics® to implement a numerical resolution of Eqs. (1). In particular, by taking advantage of the symmetry of the geometry, we assume an azimuthal dependence for the fields of the form exp(-imϕ), where m∈Z, i.e., a vector field v can be written as v(ρ,ϕ,z)=∑ v(ρ,z)exp(-imϕ) We analytically take out this azimuthal dependence, which makes the problem quite convenient to solve. This formalism is usually referred to as 2.5D technique [2], and allows to solve only (2m_max+1) 2D problems instead of solving a 3D problem, thus, significantly reducing the computational load in terms of memory and processing time. 2.5D implementation needs all fields to be expressed in terms of a azimuthal mode number m. By using this modeling technique, we numerically solve the system of Eqs. (1). As an example of application for our model, we report in Fig. 1 calculations for a plasmonic nanoshell system. The induced charge density as a function of radial distance at the lower and the higher energy resonant mode is shown in Fig. 1(a) and Fig. 1(b), respectively. Electric field norm and charge density at the cross-section plane are also shown in the insets. The spill-out effects can be clearly seen at the inner and outer boundaries of the nanoshell.

[1] C. Ciracì and F. Della Sala, Phys. Rev. B 93, 205405 (2016). [2] C. Ciracì, Y. a. Urzhumov and D. R. Smith, Opt. Express 21, 9397 (2013).