Development of a Numerical Model for Large-Scale Seasonal Thermal Energy Storage for District Heating Systems
The integration of a Thermal Energy Storage (TES) system in District Heating (DH) networks allows increasing the share of renewables in the energy scheme, but it requires a proper pre-design phase in which the modelling of the TES system is adequately driven.
The main purpose of this work is the modelling of a simple and robust tool to predict the thermal behavior of a large scale TES and its interactions with the surroundings, thus providing useful indications on the geometry of the systems and on the employed materials.
In this context, COMSOL Multiphysics® is a powerful tool that allows coupling the different domains (water, envelope and ground) through an FEM model. The fluid domain of the TES system is modeled together with part of the surrounding solid domain (the soil) whose composition and thermal properties can thus be taken into account.
A proper study of the fluid domain requires the use of momentum- and energy-conservation equations. However, the use of Computational Fluid Dynamics (CFD) in the multi-annual simulation of large structures involves a significant computational effort. The development of a simpler model using only the energy-conservation equation can be particularly useful in the early design phase, when a higher flexibility is required in terms of both geometry and materials’ characteristics.
In this work, this simplified model is used to compare TES with different aspect ratios (height to diameter). For this purpose, the Heat transfer in solids and Coefficient Form Boundary interfaces from COMSOL Multiphysics® are employed. The first one describes the surrounding ground, while the second one is adopted to implement the system of energy balance equations to describe the fluid domain (e.g. water). Moreover, the axial symmetrical modelling environment is used to reduce the number of equations.
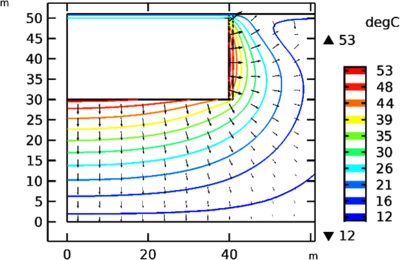
A drawback of the utilization of such a simplified model is the absence of adequate equations to describe the buoyancy: the resulting temperature profile presents, in fact, some discrepancies that are not observed in real water storage systems. The contribution of buoyancy is particularly relevant during the storage period when the temperature degradation due to the thermal losses leads to the characteristic thermal stratification. Proper adjustments (defined buoyancy sub-models) are thus applied in the presented simplified model to consider the effect of buoyancy forces on the temperature distribution and therefore on the distribution of thermal losses, which affect significantly the performance of a TES system. The observed numerical oscillations are reduced, with a proper revision of the Solver configuration e.g. damping factor, stabilization method.
Contact area, local envelope structure e.g. insulation thickness and surroundings (ambient air and ground) directly affect the amount of thermal losses from a TES system. Therefore, the variation of the aspect ratio plays an important role in the distribution of thermal losses through the various envelope elements (cover, lateral wall and bottom wall).