Predicting the Parasitic Forces in the Magnetically Levitated Adaptive Optics Mirrors
In an Adaptive Optics system, the magnetic coupling of the Deformable Mirror with the Reference Frame may generate undesired forces and torques when any mechanical misalignment occurs. Moreover, the concave or convex shape of the thin, adaptive mirror shell undergoes similar permanent static forces and torques because of the mutual interaction of the magnets. Computing such parasitic strengths is crucially important in order to evaluating undesired deformation when operating the system. This paper discusses the COMSOL Multiphysics® models and the procedures implemented in order to compute these forces and torques: the proposed numerical methods are an alternative to complex, expensive, and time-consuming experimental tests - nevertheless, a comparison with an available set of measures shows the accuracy of the proposed approach.
The three methods available to compute the magnetic forces, the integration of the Maxwell stress tensor, the Lorentz equation, and the principle of virtual work, are compared throughout the paper, in order to demonstrate the high level of accuracy of the last, which is selected as a powerful computational tool within the COMSOL Multiphysics® programmability.
After proving the reliability of the three dimensional model through a comparison with the correspondent two dimensional one, the paper shows the modelling, meshing, and computational procedures set up for three types of interactions - the magnet-to-magnet and the coil-to-magnet interaction of a single actuator and the magnet-to-magnet interaction between two closest permanent magnets. Even if more demanding in terms of degrees of freedom, the virtual work method will prove much more accuracy when the permanent magnet is a compound with different magnetization directions, in the absence of any external current. The accuracy of the results is evaluated by means of the verification of the third principle of dynamics.
As an energy-based method, the virtual work computation requires a proper definition of both the stored energy and coenergy in the hard magnetic materials. In the most general case, so including non-linear permanent magnets, such energies can be defined as either via a MATLAB® numerical integration or deploying the built-in COMSOL Multiphysics® integration operator. Finally, the default definition COMSOL Multiphysics® of the magnetic energy has been accordingly re-formulated.
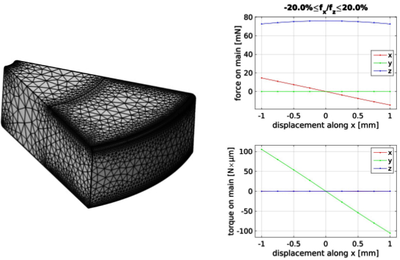
As a result of the three mentioned computational cases, the parasitic force and torques applied to the deformable mirror are shown as a function of the alignment displacement and rotation errors, as well as static disturbances throughout the atmospheric turbulence correction.
下载
- del vecchio_presentation.pdf - 6.75MB
- del vecchio_paper.pdf - 1.83MB
- del vecchio_abstract.pdf - 0.1MB
