论文和技术资料

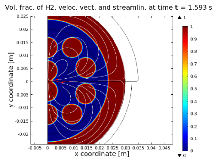
Introduction: In metal foams production, nucleated gas bubbles expand in a heated metal in a mold, then the foam cool and solidify. Thereby energy, mass and momentum transfer mechanisms are present simultaneously in the system and must be taken into account. Metal foam (Figure 1) can be obtained by foaming a precursor, i.e. a mixing of aluminum (Al) powders with the blowing agent TiH2, placing it in a mold and heated in a furnace to release gas (H2). H2 bubbles nucleate and successively expand in the melted Al, driving the mold filling. Experimental works carried out by observation techniques cannot be sometimes applied owing to the specific properties of the metals. However, the processing of this innovative material can be analyzed by applying computational techniques, although the computational work is very challenging, requiring to model and simulate transfer phenomena and phase interface movements at the same time. Use of COMSOL Multiphysics: We use COMSOL Multiphysics 4.2 to study the heat transfer, H2 gas bubbles growth in liquid Al and the resulting movement for a metal foam expanding under heat treatment in a 2D steel mold. The model considers energy transfer across the walls of the mold, as well in the Al and H2 regions. H2 diffusion causes the bubbles to grow and this is simulated by using a specific expansion rate. In the computational model, steps are set in order to foresee changes in geometry and materials properties, as consequence of bubbles nucleation and metal melting. Surface tension, densities and viscosities are considered for the Al-H2 fluid system and effective thermal properties are taken into account for all the materials. The movement of the H2 gas bubbles embedded in the viscous Al liquid is numerically simulated by using the equations of fluid dynamics coupled to the level set method. In particular, the movement of the gas in the bubble is computed with the weakly-compressible model, while the fluid dynamics of the Al is calculated using the incompressible Stokes flow equations. The model equations are solved on a two-dimensional mesh with adaptive mesh refinement in time, in order to reduce the computational complexity of the problem and well describe the strong gradients close to the gas-liquid interface. Results: Some of the obtained results are shown in Figure 2 and 3. The wall thickness influences the heat transport to the two bubbles and their expansion in the mold geometry controls the flow regime. Conclusion: In spite of the problem complexity and the needed simplifications, the computational model is very well suited to describe satisfactorily heat transfer, bubble expansion, interface movement and fluid flow during the foaming process. The influence of the mold geometry has been considered. Interesting considerations can be drawn regarding the temperature field in the system and the resulting expansion of the metal foam. We plan to improve our future work by including more bubbles and the mechanism of gas diffusion, in order to develop a more comprehensive model for foaming processes, although assessments on computing capabilities should be made.