论文和技术资料

The dependency of electrochemical processes performances on mass transfer is well-known. Electrolyte flow in the vicinity of electrodes surface can enhance reactions due to increased mass transfer. This flow can be generated by the production of a gaseous phase, leading to a natural bubble-driven convection flow. As a drawback, gas bubbles also modify electrodes active surface and the conductivity of the gas/electrolyte mixture. Since multiphase flows and electrochemistry are interdependent (two-way coupling), they lead to a high number of parameters to take into account. Process efficiency can, for example, be modified by electrodes and reactors designs, electrokinetics, pressure, production rate, reagents concentration, electrode surface conditions, etc.

The present work introduces the modeling of bubbly-flows in the typical case of alkaline water electrolysis by two vertical facing electrodes. A full hierarchy of models can be used to simulate two-phase flows, going from the Eulerian-Eulerian homogeneous (HEM), mixture (or drift flux) and two-fluid (2FM) models to the Direct Numerical Simulation (DNS) of the continuous phase with Lagrangian tracking of the bubbles. In this study, a 2D mixture model was adopted to conciliate a sufficiently accurate simulation of bubbles plumes evolution and an acceptable computational cost. The mixture formulation as expressed by Ishii [1] is based on the modeling of the dispersed-continuous mixture as a Newtonian fluid. The scalar α, namely the void fraction, is the local volume-averaged proportion of gaseous phase in the mixture. The closure term for the calculation of void fraction diffusion in the mixture is the drift flux (or relative velocity), of which constitutive equation can be found in the work of Wedin and Dahlkild [2]. It is written as a sum of various mechanisms, documented in the literature [3–6].

Simulations of bubbly-driven and convective two-phase steady flows are done with COMSOL Multiphysics® software by means of a modified Non-Isothermal Flow interface to resolve both the hydrodynamics and the diffusion of a scalar. Electrochemical generation of bubbles at the walls is simulated, either by a uniform flux approximation, or by the resolution of the electrolyte potential and appropriate electro-kinetical laws.

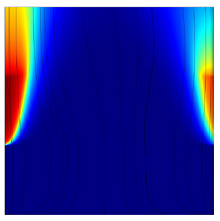
Simulation results are compared to the experimental work of Boissonneau & Byrne [7], who ran alkaline water electrolysis in a vertical channel under bubbly-driven convection. Simulated velocity fields show a good agreement with measured velocities (Figure 1). A new model is derived from the mixture formulation by a proper scale analysis. In analogy with thermal natural convection, dimensionless Rayleigh-like and Prandtl-like numbers are defined to characterize the naturally occurring flow induced by wall-bounded gas production between vertical electrodes [8]. Scaling laws of plume thickness evolution are proposed for both bubbly-driven and forced convection configurations. Computations of the mixture model in COMSOL for a wide range of Prandtl-like numbers show that the relative plume thickness can faithfully be related to Reynolds (Figure 2) and Rayleigh-like (Figure 3) numbers.

This work gives insight on the different mechanisms leading plume dispersion; it highlights the most influent process parameters and shows that the electrochemically generated two-phase flows can be efficiently controlled by them.