论文和技术资料

Introduction:

The numerical solution to the neutron transport equation is employed to study a variety of problems in nuclear engineering applications, including for both eigenvalue and fixed source studies. Historically, multiphysics analysis at the HFIR has utilized these solutions to include thermal-structural and thermal hydraulic physics with a weak coupling due to the limited availability of the neutron flux profile (from stochastic solutions) and its cumbersome import from a separate code/solver. However, increasing computational power and advances in versatile and custom simulation environments (i.e. COMSOL Multiphysics® software) allow for a direct coupling of neutron transport solutions for more comprehensive multiphysics analyses. Establishment and verification of baseline and benchmark neutron transport solutions (see Figure 1) against existing validated code results and analytical solutions is an important first step in confirming COMSOL software as a capable tool for this type of application.

Use of COMSOL Multiphysics:

The COMSOL Application Builder and Weak Form PDE physics interface are utilized in multiple geometric dimensions (1D, 2D, 2D axisymmetric and 3D) to solve the multi-group discrete ordinate neutron transport equations for the neutron flux. Due to the high number of coupled field equations and corresponding boundary constraints, which is a product of the chosen number of discretized energy groups and angular quadratures, as well as the time-consuming import of nuclear data (cross sections) into the COMSOL software, an automated use of the COMSOL Application Builder (see Figure 2) to create these custom models is favored. After creation of an intermediary application model file, the manual geometry, solver, and mesh development occur within a customary COMSOL model file that is saved for final use. A stationary solver is used to calculate the steady-state neutron flux and a coupled global ODE for the effective multiplication factor. To accelerate convergence, a few-group neutron diffusion equation eigenvalue solution to the problem may be solved and used as an input to the stationary solver. The direct PARDISO solver is used for the eigenvalue calculation (if computed) and the MUMPS solver is used for the stationary calculations in order to utilize parallel computing.

Results and Conclusions:

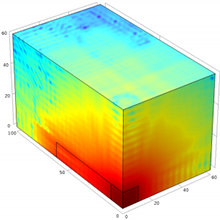
A focus of this work is the Kobayashi benchmarks for 3-D radiation transport problems, which have estimated analytical solutions and a variety of code results for comparison. Difficult problems for discrete ordinates solutions (due to ray effects) involving large low-scattering regions and small, isolated fixed sources, create expected discrepancies in the results (see Figure 3). Simpler problems with multiplying regions are also computed and compared to available and validated codes using the same nuclear data (see Figure 4).