Considerations for Detailed Finite Element Analyses
Speaker driver design usually requires a full and detailed electrovibroacoustic analysis in order to understand how some key design variables affect the electromagnetic properties, the vibration behavior of the moving parts, and the sound radiation pattern generated. Analysis that includes all of the acting electromagnetic and mechanical components of a driver allows you to understand the linear behavior of the driver; to optimize the dimension, shape, or topology of a specific component in the driver; or to study the nonlinear distortion when deformation becomes large.
To perform electrovibroacoustic analysis in the COMSOL Multiphysics® software, you need to solve a fully coupled problem that combines the electromagnetic field with structural vibrations and acoustic radiation. The finite element method (FEM) is the most often used approach at this stage, and COMSOL Multiphysics® has built-in features that couple the physics interfaces for modeling different types of speaker drivers, as described in our blog post “Modeling Speaker Drivers: Which Coupling Feature to Use”. Here, we use a conventional dynamic speaker driver as an example and discuss the important concepts in setting up a multiphysics FEM model for speaker driver analysis.
Background and Introducing the Example
A typical dynamic transducer is composed of a permanent magnet, which is responsible for generating the magnetic field, and a multiturn coil placed within this field. When an AC voltage (current) is applied to the coil, an electromagnetic force — referred to as the Lorentz force — is generated. This force induces vibrations in the coil and the connected diaphragm, leading to sound being radiated.
Conversely, the coil's motion within the magnetic field triggers a voltage induction within the coil. This phenomenon, known as back EMF (EMF being electromotive force), subsequently influences the magnetic field. This interplay of forces and induced voltages is the foundational mechanism behind conventional dynamic speaker drivers that are based on moving coils.
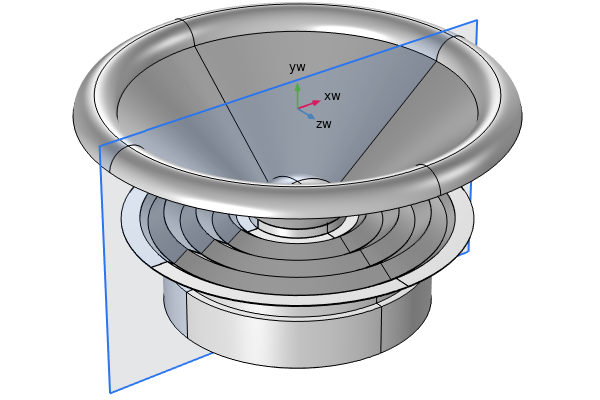
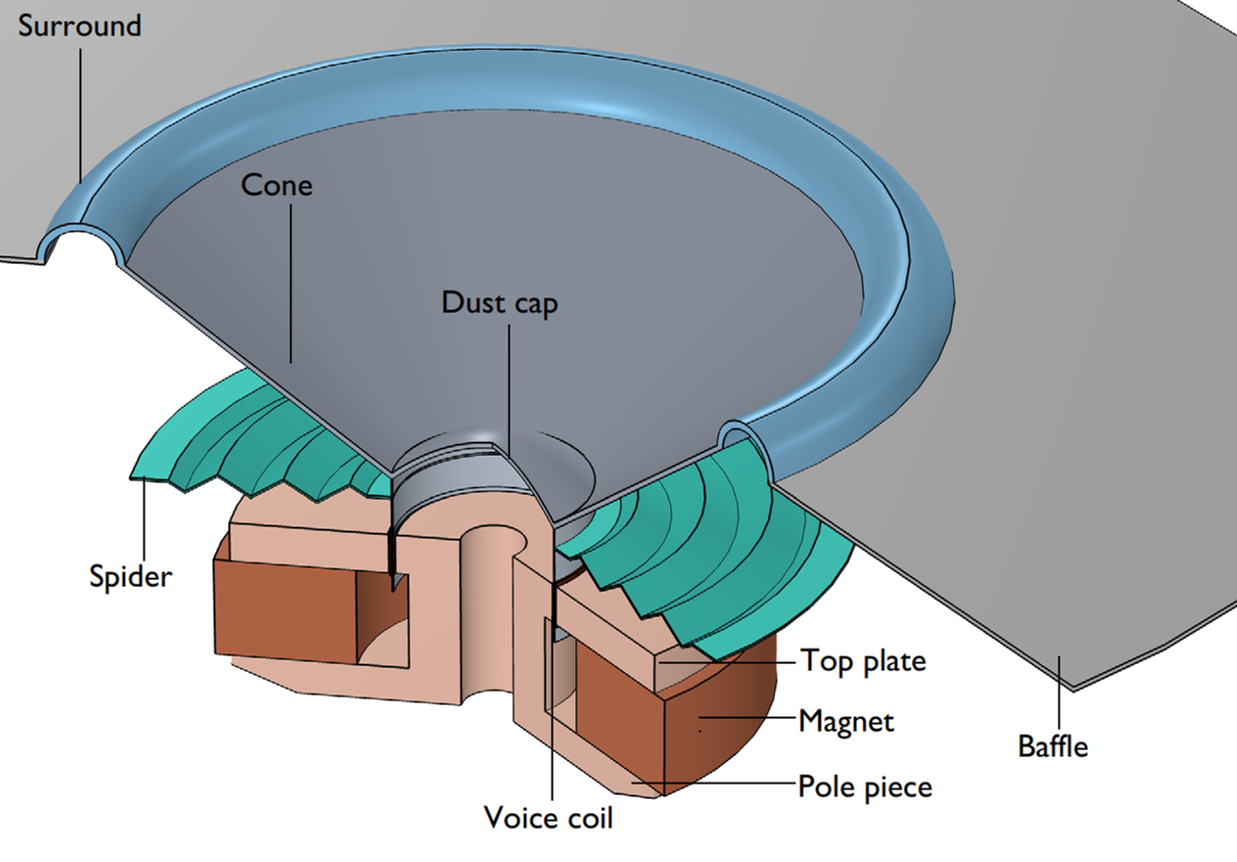 A moving coil transducer uses Lorentz force to induce vibration
A moving coil transducer uses Lorentz force to induce vibration
Solving the Problem in Frequency Domain or Time Domain
The magnetic field in a dynamic transducer includes two components, a static component induced by the permanent magnet and an oscillatory component generated from the AC current in the voice coil. Modeling the contribution from both requires a two-step study: First, a Stationary study step is necessary for solving the static magnetic field induced by the magnet. This should be followed by a second study step for computing the perturbed solution of all fields around the bias solution computed in the first step.
The second study step can either be a Frequency-Domain, Perturbation study or a Time Dependent study based on the characteristics of both the excitation and solution. A Frequency-Domain, Perturbation study type is applicable under the following conditions:
- The oscillatory excitation is harmonic and continuous
- The magnitude of oscillation is small and the system stays linear
- The output of interest is the steady-state time-harmonic solution
- The study is used for computing the response of a linear or linearized model subjected to harmonic excitation around a bias for one or multiple frequencies.
Should any of these conditions fail to hold, a Time Dependent study should be used in the second step. This would be necessary under the following circumstances:
- If the excitation takes the form of a short pulse or includes more than one frequency component.
- If the system introduces a nonlinearity. The nonlinearity can be due to large signal excitation and higher harmonic generation, a nonlinear magnetization model, or geometry change because of large deformation.
- The output of interest is the transient response to an excitation, rather than a steady-state time-harmonic solution.
To create the two-step study, you can first select the Stationary study type from the Preset Studies for Some Physics Interfaces option in the Select Study window of the Model Wizard. The second study step will be manually added in the Model Builder later.
For the Frequency-Domain, Perturbation analysis, you also have the option to choose Small-Signal Analysis, Frequency Domain from Magnetic Fields in the Select Study window in the Model Wizard, as shown in the image below. This study consists of the required two study steps: a Stationary study step for computing the biased solution, followed by a Frequency-Domain, Perturbation study step for computing the frequency response about the biased solution.
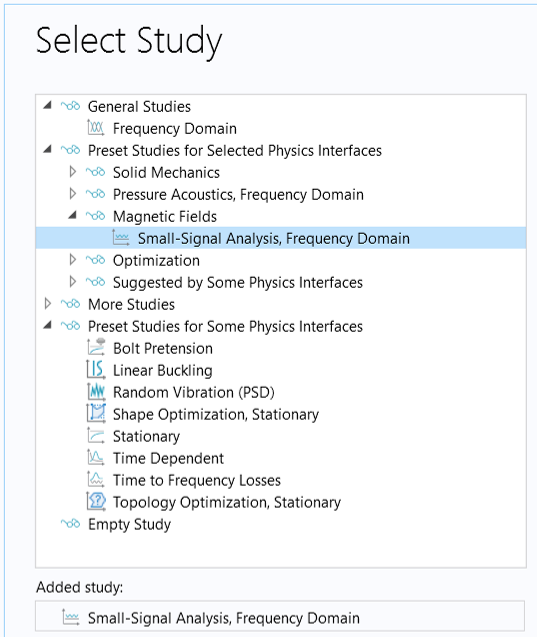
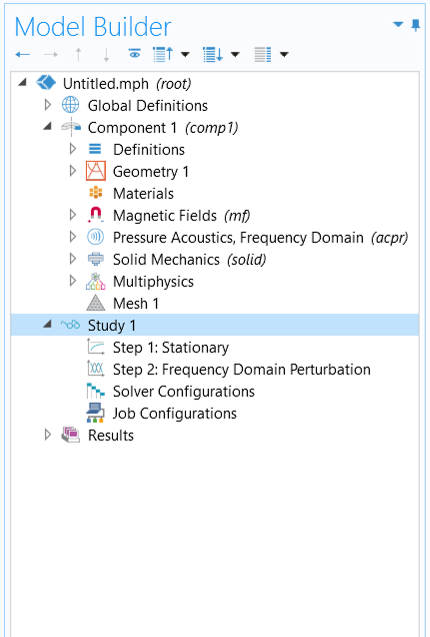
Selecting the Small-Signal Analysis, Frequency Domain study from the Select Study window (left) and the resulting study steps added to the model tree (right).
In Part 2 of this course, we will learn how to run a frequency-domain analysis. Then, in Part 4, we will look at setting up a transient model.
Solving the Problem in 2D or 3D
For structures with axial symmetry, a 2D axisymmetric model often suffices, assuming that the load conditions, boundary conditions, and the solution of interest exhibit the same symmetry. This applies to conventional dynamic drivers characterized by rotational symmetry (for instance, models that do not have a basket). Such models are especially useful when the aim is to capture the axisymmetric modes excited in both solid and fluid components. Implementing a 2D model considerably reduces the computational load, whereas you can easily visualize the results in a full 3D geometry using a Revolution 2D dataset.
When a 2D axisymmetric model is not suitable, and a 3D model is required, check if your geometry has any symmetry (or near symmetry) and decide whether you anticipate that the solution will have similar symmetry. Taking advantage of symmetry enables you to model just a portion of the geometry, significantly reducing the complexity of a 3D model. The images below illustrate various geometry scenarios: 2D axisymmetry applied when the 3D geometry is entirely axisymmetric (left image); 3D modeling of a quarter of the geometry when a basket is incorporated, leveraging symmetries (middle); and a 3D model using a 60-degree sector when using sector symmetries (right). In these examples, the speaker driver is assumed to be placed in an infinite baffle.
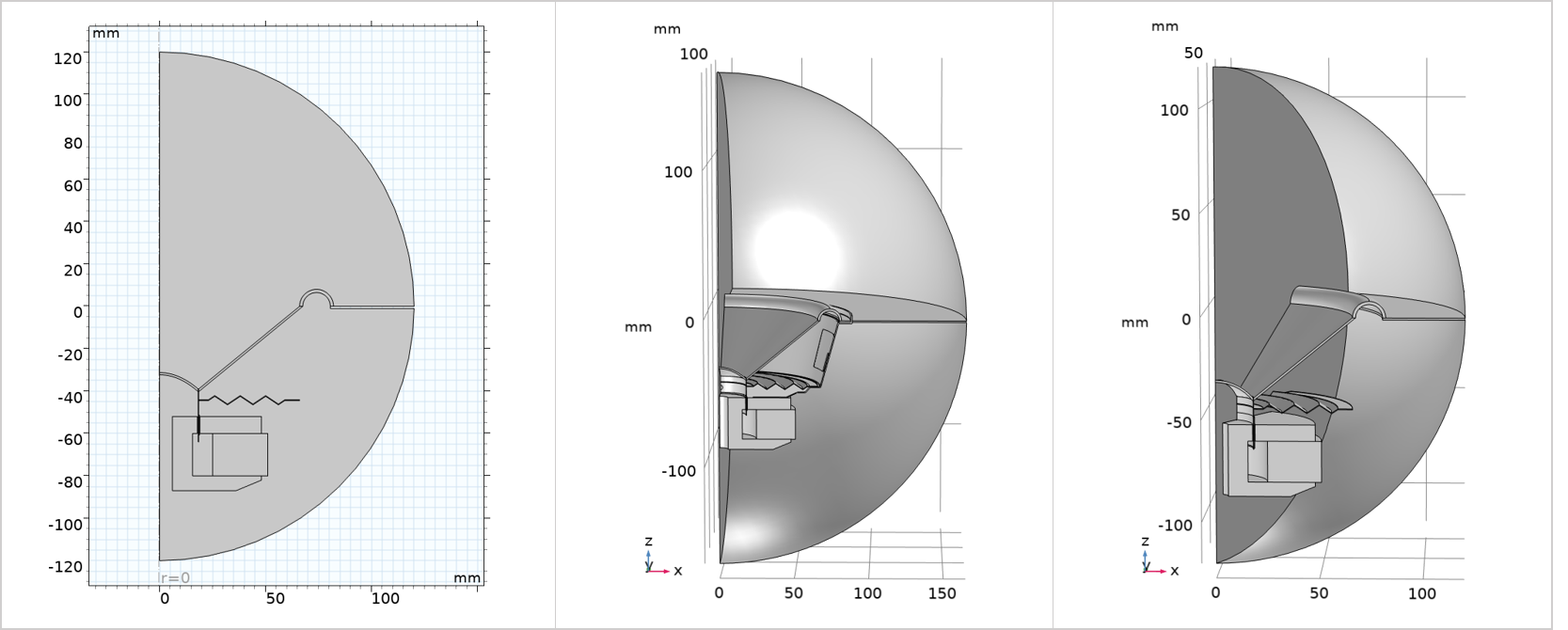 Geometries for solving the problem in 2D axisymmetry (left), 3D with a quarter of the geometry by using symmetries (middle), and 3D with a 60-degree sector by using sector symmetries (right).
Geometries for solving the problem in 2D axisymmetry (left), 3D with a quarter of the geometry by using symmetries (middle), and 3D with a 60-degree sector by using sector symmetries (right).
Extracting 2D Geometry From a 3D CAD
If you are working with a 3D CAD file and want to solve the model within a 2D axisymmetric space dimension, you can extract a cross section from the 3D model for 2D analysis. The following steps and images outline how to achieve this:
- In a 3D component, import the 3D CAD geometry.
- Use a Work Plane feature and set the plane to align with the cross section of the driver.
 The Model Builder with the Work Plane feature selected, the corresponding Settings window, and the driver model in the Graphics window.
A work plane is defined to specify a cross section of the 3D object.
The Model Builder with the Work Plane feature selected, the corresponding Settings window, and the driver model in the Graphics window.
A work plane is defined to specify a cross section of the 3D object.
- Add a 2D axisymmetric component (Component 2 - 2D Axisymmetry) to the model.
- Use a Cross Section feature and select the work plane defined in Geometry 1 of Component 1 - 3D for the cross section from the Work Plane list.
 The COMSOL Multiphysics UI showing the Model Builder with the Cross Section feature selected, the corresponding Settings window, and the Graphics window showing the 2D cross section.
The Cross Section feature is used to create a 2D cross section from an intersection between a 3D geometry and a work plane.
The COMSOL Multiphysics UI showing the Model Builder with the Cross Section feature selected, the corresponding Settings window, and the Graphics window showing the 2D cross section.
The Cross Section feature is used to create a 2D cross section from an intersection between a 3D geometry and a work plane.
- You can then add fluid domains to the 2D geometry for multiphysics analysis.
 The COMSOL Multiphysics UI showing the Model Builder with the Form Union setting selected, the Form Union/Assembly settings window, and the Graphics window with the 2D geometry.
The final geometry for the 2D analysis.
The COMSOL Multiphysics UI showing the Model Builder with the Form Union setting selected, the Form Union/Assembly settings window, and the Graphics window with the 2D geometry.
The final geometry for the 2D analysis.
The steps are demonstrated in the attached Extract_2D_geo_from_3D.mph file.
The Required Physics Interfaces and Multiphysics Couplings
A full electrovibroacoustic analysis of the dynamic transducer requires using the Magnetic Fields interface in the AC/DC Module to model the electromagnetic field. It also requires using one of the Acoustic-Structure Interaction multiphysics interfaces in the Acoustics Module to model vibrations of the moving parts and the sound radiating into the surrounding air.
The Magnetic Fields Interface
The Magnetic Fields interface, found under the AC/DC > Electromagnetic Fields branch in the Select Physics page of the Model Wizard, is used to compute the magnetic field and induced current distributions in and around coils, conductors, and magnets.
 The Magnetic Fields interface in the Select Physics window.
The Magnetic Fields interface in the Select Physics window.
The physics interface solves Maxwell’s equations and is used to compute, for example, the electric, , and magnetic,
, fields.
The Magnetic Fields interface requires the following material properties:
- The electrical conductivity,
- The relative magnetic permeability,
, or the magnetization vector,
- The relative permittivity,
- The velocity of the moving coil,
- The remanent flux density of the magnet,
- The B-H curve of the top plate and pole piece
- The coil properties, including the number of turns, the coil wire conductivity, and its cross-section area
- The externally generated current density,
- The frequency,
(for a time-harmonic analysis)
The Acoustic–Structure Interaction Multiphysics Interfaces
There are multiple multiphysics interfaces in the Acoustic-Structure Interaction branch that can be used to model coupled vibrations and sound radiation. The interfaces used most often are the Acoustic-Solid Interaction, Frequency Domain interface for frequency-domain analysis and the Acoustic-Solid Interaction, Transient interface for performing a time-dependent study. The following image shows the location of these interfaces in the Select Physics window of the Model Wizard.
 The Acoustic-Solid Interaction multiphysics interfaces are under the Acoustics > Acoustic-Structure Interaction branch of the Select Physics page in the Model Wizard.
The Acoustic-Solid Interaction multiphysics interfaces are under the Acoustics > Acoustic-Structure Interaction branch of the Select Physics page in the Model Wizard.
The Acoustic-Solid Interaction multiphysics interfaces combine the Pressure Acoustics and Solid Mechanics interfaces to connect the acoustic pressure variations in a fluid domain with the structural deformation in a solid domain. When selecting this type of multiphysics interface, the Acoustic-Structure Boundary multiphysics coupling feature is automatically added to the model. This multiphysics coupling is used to connect a Pressure Acoustics model to any structural component.
You also have the option to add the acoustics and structural physics one at a time and then combine them by manually adding the Acoustic-Structure Boundary coupling, which is readily available in the multiphysics selection list that appears after right-clicking the Multiphysics node in the model tree.
The Pressure Acoustics interface solves a scalar wave equation for the total acoustic pressure, , while the Solid Mechanics interface solves Newton’s second law of motion for the structural displacement field,
.
The Pressure Acoustics interface requires the following material properties:
- The density,
- The speed of sound,
- The monopole domain source,
(provides an option to add a domain mass source when applicable; the default value is zero)
- The dipole domain source,
(provides an option to add a domain force source when applicable; the default value is zero)
- The frequency,
(for a time-harmonic analysis)
- Damping parameters when a lossy fluid model is used to include bulk damping
The Solid Mechanics interface requires the following material properties:
The density,
A pair of elastic moduli for isotropic materials, or for anisotropic materials, either an elasticity matrix or a compliance matrix
The body force,
The frequency,
(for a time-harmonic analysis)
Damping parameters when mechanical damping is included
The Acoustic-Structure Boundary coupling includes the fluid load on the structure and the structural acceleration as experienced by the fluid. The image below shows an example of an Acoustic-Structure Boundary coupling used in a loudspeaker driver simulation.
 The COMSOL Multiphysics UI showing the Model Builder with the Acoustic-Structure Boundary feature selected, the corresponding Settings window with a coupling between the Pressure Acoustics, Frequency Domain interface and Solid Mechanics interface set up, and the corresponding 2D model in the Graphics window.
The Acoustic-Structure Boundary multiphysics coupling connects a pressure acoustics model to any structural component.
The COMSOL Multiphysics UI showing the Model Builder with the Acoustic-Structure Boundary feature selected, the corresponding Settings window with a coupling between the Pressure Acoustics, Frequency Domain interface and Solid Mechanics interface set up, and the corresponding 2D model in the Graphics window.
The Acoustic-Structure Boundary multiphysics coupling connects a pressure acoustics model to any structural component.
The Lorentz Coupling
To calculate the Lorentz force and back EMF, use a Lorentz Coupling feature, which is a multiphysics coupling between the Magnetic Fields interface and the Solid Mechanics interface.
When modeling dynamic drivers, the coupling is typically added in the voice coil domains, as seen in the image below. It passes the Lorentz force from the Magnetic Fields interface to the Solid Mechanics interface and passes the structural velocity — which leads to the induced electric field — from the Solid Mechanics interface to the Magnetic Fields interface.
 The COMSOL Multiphysics UI showing the Model Builder with the Lorentz Coupling feature selected, the corresponding Settings window, and the Graphics window showing a close-up of the 2D model.
The Lorentz Coupling connects the magnetic fields with solid mechanics to calculate the Lorentz force and back EMF.
The COMSOL Multiphysics UI showing the Model Builder with the Lorentz Coupling feature selected, the corresponding Settings window, and the Graphics window showing a close-up of the 2D model.
The Lorentz Coupling connects the magnetic fields with solid mechanics to calculate the Lorentz force and back EMF.
Other Physics Interface Options for Structural Vibrations and Acoustics
Modeling Thin Structures Using the Shell Feature
When there are thin objects in the system subject to vibrations, using the Shell feature can vastly reduce the number of mesh elements required to resolve the model. The Shell interface is available for 3D and 2D axisymmetric analysis. You can consider using it for thin components, including the cone, the surround, the spider, and the former, as well as thin mounting panels like cabinet walls if applicable. However, the coil object needs to be modeled as a solid domain using a Solid Mechanics interface since the Lorentz Coupling feature is only applicable for coupling the Magnetic Fields interface with the Solid Mechanics interface.
The Acoustic-Structure Boundary coupling is also applicable for coupling a Pressure Acoustics model with a Shell model. When the shells are interior structures with fluid on both sides, a slit is added to the pressure variable and care is taken to couple the ’up’ and ‘down’ sides such that the acoustic load is given by the pressure drop across the thin structure.
Solid–Thin Structure Connection
When both the Shell and Solid Mechanics interfaces are used, the Solid-Thin Structure Connection multiphysics coupling feature can be added to create transitions between domains modeled using the Solid Mechanics interface and boundaries modeled using the Shell interface. See an example in the Loudspeaker Driver in a Vented Enclosure tutorial model.
 The COMSOL Multiphysics UI showing the Model Builder with the Solid-Thin Structure Connection feature selected, the corresponding Settings window, and the model in the Graphics window.
The Solid-Thin Structure Connection couples shells and solids.
The COMSOL Multiphysics UI showing the Model Builder with the Solid-Thin Structure Connection feature selected, the corresponding Settings window, and the model in the Graphics window.
The Solid-Thin Structure Connection couples shells and solids.
The Shell and Solid-Thin Structure Connection features require the Structural Mechanics Module.
Modeling Thermoviscous Boundary Layer Losses
When sound propagates in structures and geometries with small dimensions, the sound waves become attenuated because the losses occur in the acoustic thermal and viscous boundary layers near the walls. Including these losses are important. In order to accurately model the response of small transducers, like miniature loudspeakers (especially when operated around resonant frequencies), it is important to include these losses.
COMSOL® provides three ways to model thermoviscous boundary layer losses:
Use the Narrow Region Acoustics feature with the Pressure Acoustics, Frequency Domain interface. This defines a fluid model in channels and ducts of constant cross section. The losses due to the viscous and thermal dissipation in the acoustic boundary layer are homogenized and smeared on the fluid. Although applicable only in waveguides of constant cross section, it is suitable for all frequencies, that is, also the very narrow case where boundary layers are overlapping. Examples of this option include the Loudspeaker Driver - Frequency Domain Analysis, Balanced Armature Transducer - Frequency Domain Analysis, and OW Microspeaker: Simulation and Correlation with Measurements tutorials.
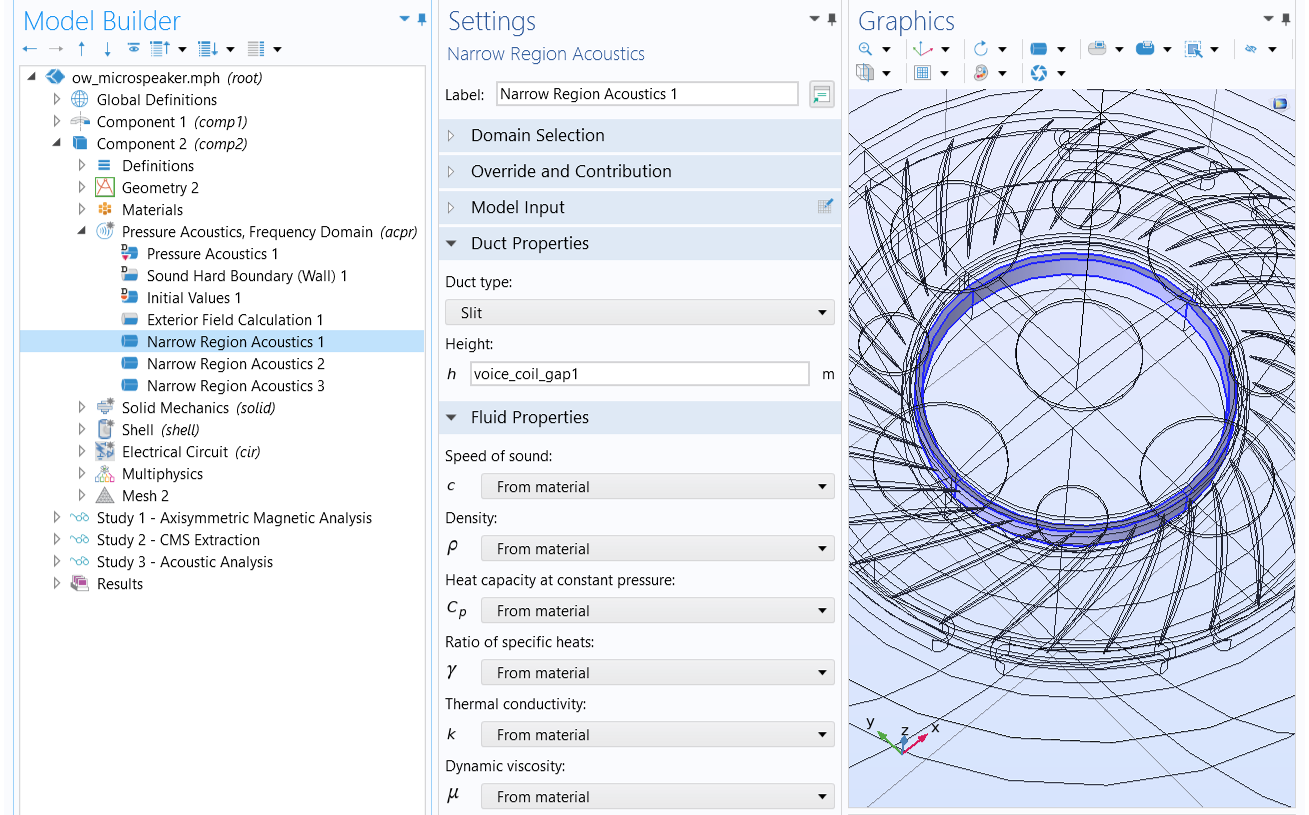 An example of using Narrow Region Acoustics to capture the thermoviscous damping in small fluid channels of constant cross section.
An example of using Narrow Region Acoustics to capture the thermoviscous damping in small fluid channels of constant cross section.
Use the Thermoviscous Boundary Layer Impedance feature with the Pressure Acoustics, Frequency Domain interface. With this feature, the losses are integrated through the boundary layers in an analytical manner. This feature is not suitable for geometry with overlapping boundary layers, such as geometry with very curved boundaries or very narrow waveguides (where the dimensions are comparable to the boundary layer thickness). Other than these cases, there are no restrictions for when this feature can be used with a certain geometry shape. See a demonstration of this feature in the Ear Canal Acoustics and Type 4.3 Ear Simulator tutorials.
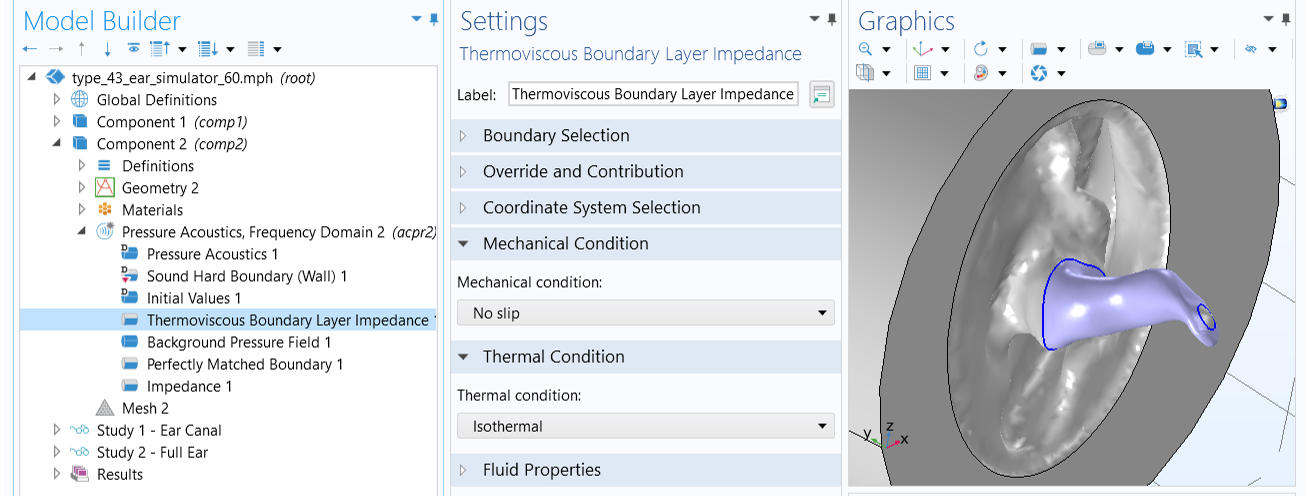 An example of using the Thermoviscous Boundary Layer Impedance feature to capture the thermoviscous damping in small fluid channels where boundary layers are not overlapping.
An example of using the Thermoviscous Boundary Layer Impedance feature to capture the thermoviscous damping in small fluid channels where boundary layers are not overlapping.
Use a thermoviscous acoustics physics interface that models the acoustic behavior in the thermoviscous boundary layer in detail. It solves a full set of linearized governing equations including explicitly thermal conduction effects and viscous losses. Not limited to any geometry and dimension, this option works for the full frequency range and supports both the frequency domain and transient analysis. Examples include the Piezoelectric MEMS Speaker and the Electrostatic Speaker Driver tutorial models.
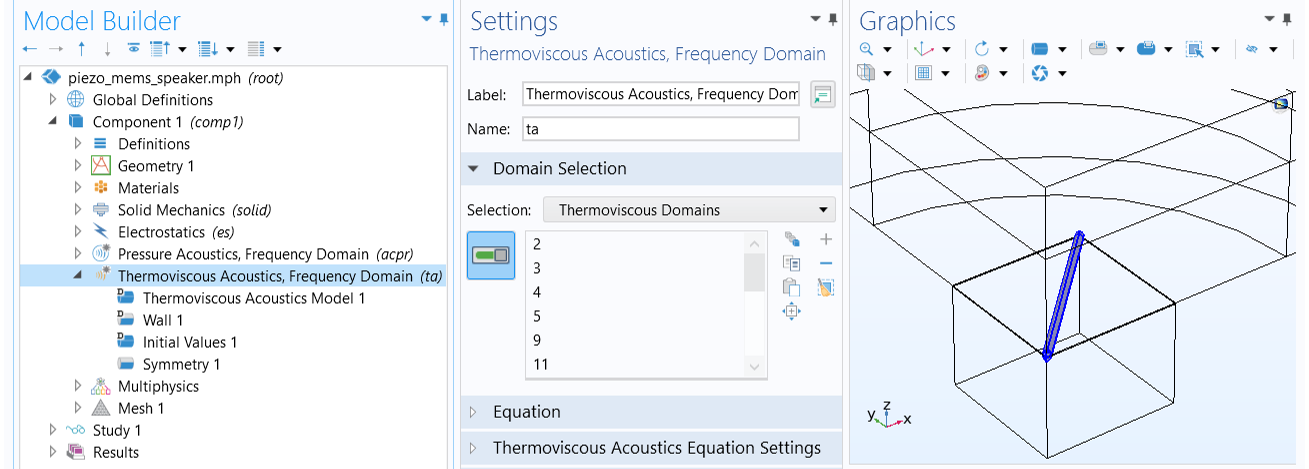 The full thermoviscous acoustic model is used to simulate the acoustic behavior in the narrow gaps of air between the triangular membranes of a piezoelectric MEMS speaker.
The full thermoviscous acoustic model is used to simulate the acoustic behavior in the narrow gaps of air between the triangular membranes of a piezoelectric MEMS speaker.
In addition, note that in order to solve a thermoviscous acoustic model, you must solve for the acoustic pressure; the velocity field (has 3 components in a 3D model); and temperature variations. With this many dependent variables, your acoustics model may be computationally expensive and require many degrees of freedom (DOFs). It is therefore recommended that you first check if you are able to use the first two effective options before turning to the full thermoviscous formulation.
Thermoviscous Acoustic–Structure Boundary
The Thermoviscous Acoustic-Structure Boundary feature is used to couple a Thermoviscous Acoustics interface with any structural component. The coupling prescribes continuity in the displacement field at the fluid–structure boundaries.
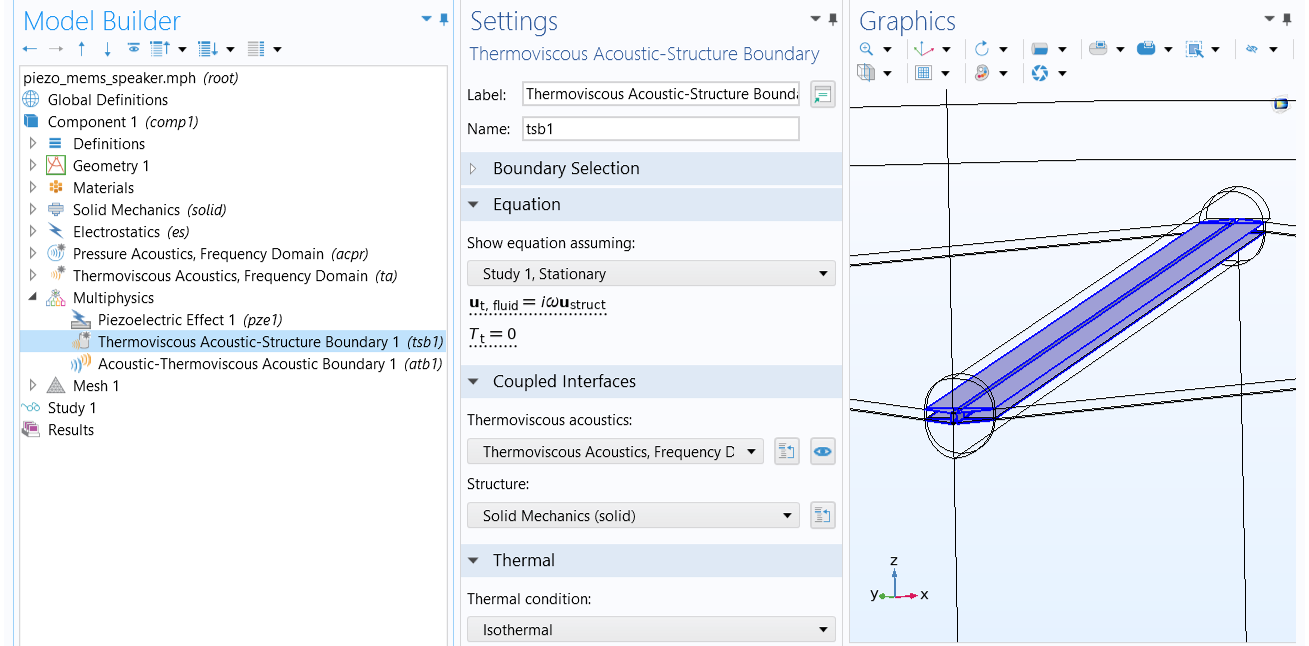 The Thermoviscous Acoustic-Structure Boundary coupling prescribes continuity in the displacement field at the fluid–structure boundaries.
The Thermoviscous Acoustic-Structure Boundary coupling prescribes continuity in the displacement field at the fluid–structure boundaries.
Acoustic–Thermoviscous Acoustic Boundary
As it is only necessary to solve the fully-detailed thermoviscous acoustics model near walls in the boundary layer region, it makes sense to switch to classical pressure acoustics outside this region. This approach saves a lot of memory and solution time due to the reduced number of degrees of freedom. In this case, you can use the Acoustic-Thermoviscous Acoustic Boundary coupling feature to couple a Thermoviscous Acoustics interface with a Pressure Acoustics interface.
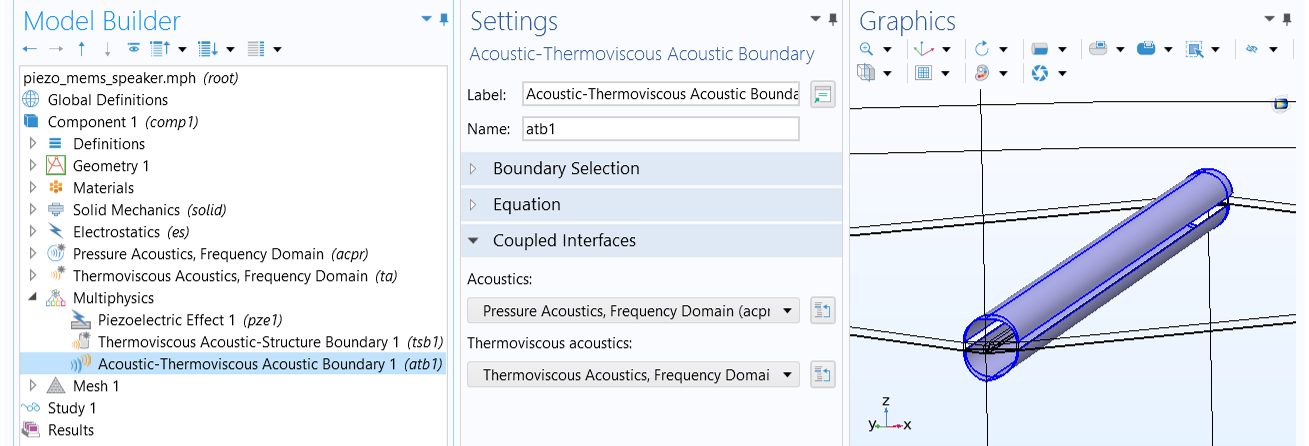 The Acoustic-Thermoviscous Acoustic Boundary coupling connects a thermoviscous acoustics model with a pressure acoustics model.
The Acoustic-Thermoviscous Acoustic Boundary coupling connects a thermoviscous acoustics model with a pressure acoustics model.
The coupling prescribes continuity in the total normal stress (dynamic condition) and the total normal acceleration for the mechanical part (kinematic condition). An adiabatic condition is prescribed for the total temperature to match the physical assumptions of the pressure acoustics formulation.
Further Learning
Read the following blog posts to learn more about thermoviscous acoustics and the multiphysics coupling features in COMSOL Multiphysics® for modeling different types of speaker drivers:
- Theory of Thermoviscous Acoustics: Thermal and Viscous Losses
- How to Model Thermoviscous Acoustics in COMSOL Multiphysics
- Modeling Speaker Drivers: Which Coupling Feature to Use
Also see Supplement A - Equations for additional information.
请提交与此页面相关的反馈,或点击此处联系技术支持。