使用哪种耦合特征对扬声器驱动器进行建模？

扬声器驱动器是利用电磁力产生振动并辐射声音的电声换能器。市场上各种类型的驱动程序根据不同的原理工作。在这篇博文中，我们介绍了 COMSOL Multiphysics^® 软件中内置的多物理场耦合特征，用于对扬声器驱动器进行建模。

扬声器驱动器的类型

下面列出了四种常见的驱动器类型，它们是基于不同的物理原理设计的扬声器驱动器代表：

1. 传统的动态换能器，利用施加在载流音圈上的洛伦兹力来移动音圈和附属的振膜。它们也被称为动圈换能器，是当今最流行的扬声器驱动器类型。
2. 主要用于助听器和入耳式设备的平衡电枢接收器，其运动是由磁体之间存在的麦克斯韦应力引起的。它们属于动铁扬声器类别，是最早发明的电动扬声器类型。
3. 使用压电材料的压电驱动器，例如某些类型的晶体，在外加电场产生的内部产生的机械应力下变形。它们经常用于电子设备中产生声音，并且在一些较便宜的扬声器系统中也用作高音扬声器。
4. 静电驱动器，利用施加在悬挂在两个穿孔金属片之间的又大又薄的导电隔膜板上的静电力。由于具有低失真度和高质量清晰度，它们一直受到发烧友的欢迎，并且通常比其他类型更昂贵。

尽管这些扬声器背后的驱动力都属于电磁力的范畴，但每种类型都有其独特的物理性质。动态换能器和平衡电枢接收器在磁场中工作，因此在 COMSOL Multiphysics^® 软件中对它们进行建模需要将固体力学 接口与磁场 接口耦合。另一方面，压电驱动器和静电驱动器在电场中工作，因此需要将固体力学 接口与静电 接口耦合。

COMSOL Multiphysics 内置的多物理场耦合特征，可以对所有这 4 种类型的扬声器驱动器进行建模。接下来，我们来详细了解每一种类型驱动器的建模。

洛伦兹耦合

当导体置于磁场中并通电时，一个电磁力，指定为洛伦兹力 会被施加在导体上并使其移动。另一方面，导体通过磁场的运动会引起感应电压，这种现象称为反电动势，反过来会影响磁场。这就是使用动圈的传统电动扬声器驱动器的工作原理。

这些动圈换能器包含用于产生磁场的永磁体和放置在磁场中的线圈。当向线圈施加交流电压时，由于洛伦兹力的变化，它们会来回移动，导致连接的膜片振动并发出声音。

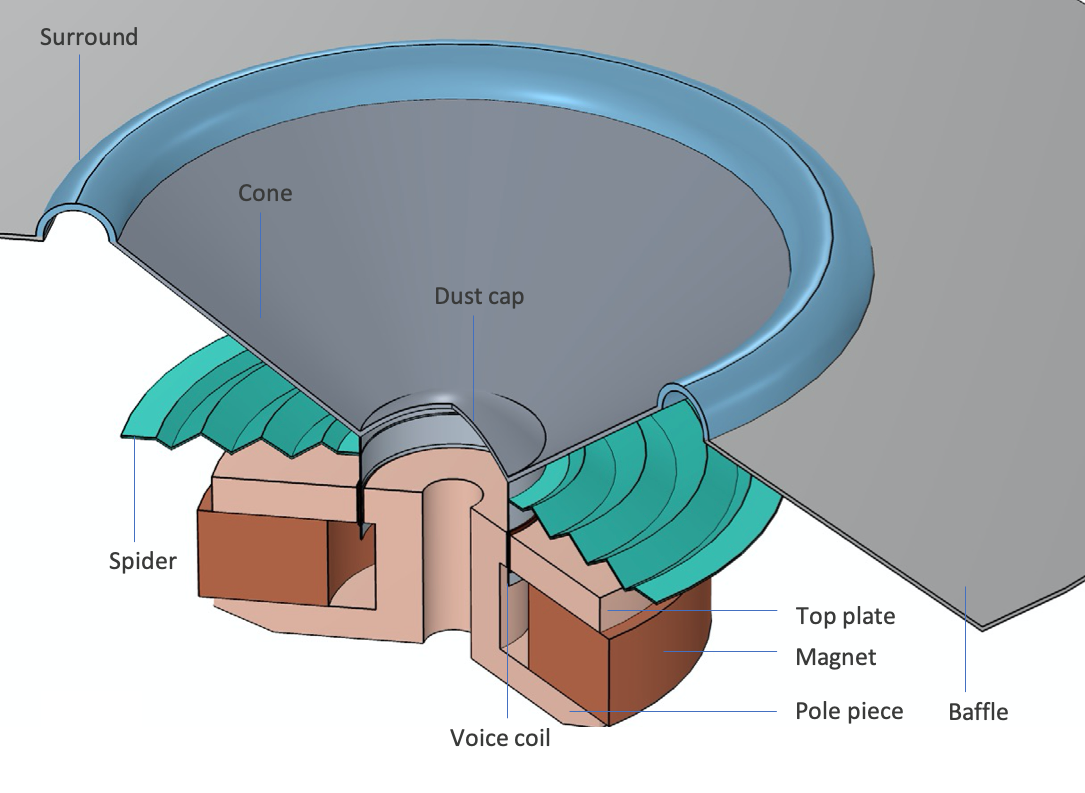
动圈换能器使用洛伦兹力来触发振动。

COMSOL 软件的洛伦兹耦合 特征通过计算洛伦兹力和反电动势来捕获这种双向效应。它是磁场 接口和固体力学 接口之间的多物理场耦合特征，用于将洛伦兹力从磁场 接口传递到固体力学 接口，并将感应电场从固体力学 接口传递到磁场 接口。洛伦兹力和感应电场使用下面的公式计算：

其中，\sigma 是电导率，\textbf E 是施加的电场，\textbf v 是动圈的速度，\textbf B 是磁通密度，\textbf v\times \textbf B 是感应电场。总电流密度 \textbf J，包括来自外加电场和感应电场的贡献，用于计算洛伦兹力 \textbf F。

在对扬声器驱动器进行建模时，通常会在音圈域中添加耦合，如扬声器驱动器-频域分析和扬声器驱动器-瞬态分析 教程案例所示。

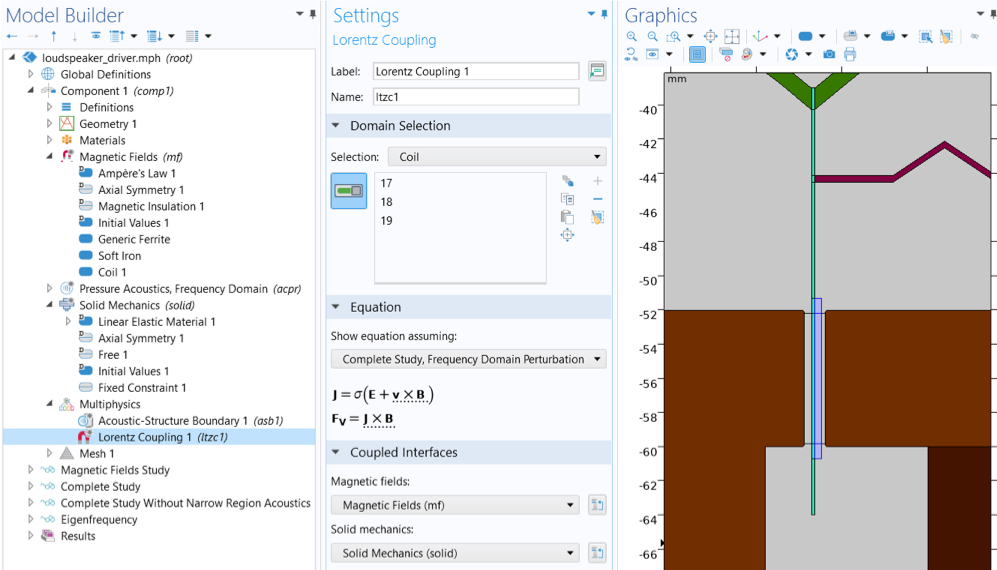
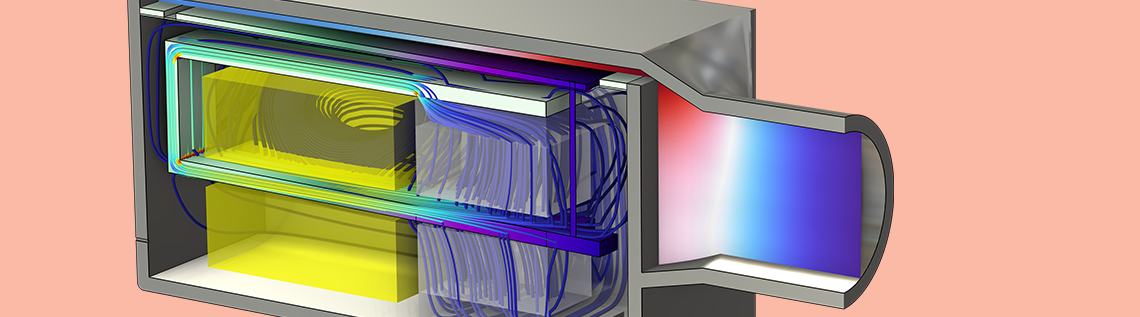
在扬声器驱动器-频域分析教程示例中，使用 洛伦兹耦合特征对动态动圈换能器进行建模。

磁力作用力

平衡电枢接收器也由磁铁、线圈和隔膜制成。但是，它是在完全不同的机理下运行的。在这类设备中，线圈是固定的，根本不会移动。

单个平衡电枢接收器包含一个小电枢(臂)，它被放置在一个音圈内，在两个磁铁之间保持平衡。当交流电流通过线圈时，电枢被磁化并处于麦克斯韦应力 下，即磁体之间存在的电磁力。该电磁力导致电枢振动并从一个磁铁移动到另一个磁铁。由于电枢连接到隔膜，其振动会传递到隔膜上，从而产生声波。

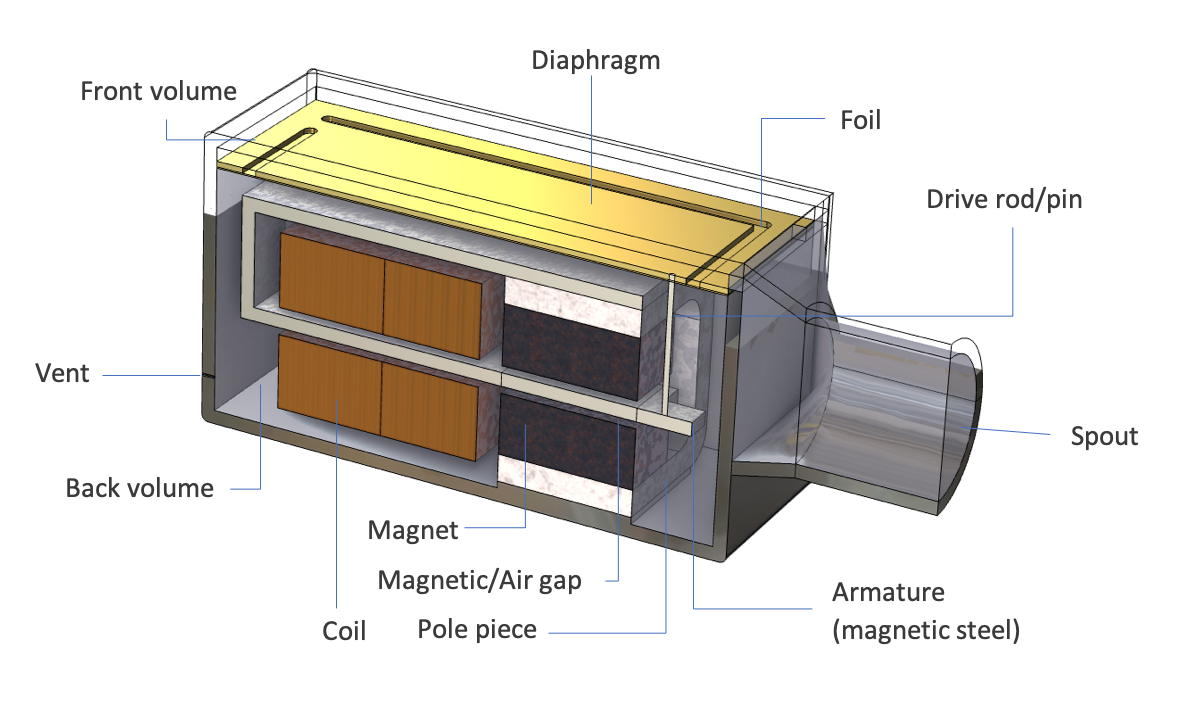
平衡电枢接收器，利用磁体之间的麦克斯韦应力来触发振动。

这个物理现象可以用 COMSOL 软件中的磁力耦合 特征捕获。该特征是磁场 接口和固体力学 接口之间的另一个多物理场耦合，用于计算施加在磁化可变形固体上的麦克斯韦应力，以及结构变形对材料磁化的影响。应力包括导致固体变形的两个分量：磁化体内存在的应力，以及与周围磁场相互作用产生的应力。前者被建模为体载荷，后者被当作一个实体外部边界上的边界载荷施加。

对于有限变形，固体中电磁应力和材料磁化强度的表达式可以使用下面被称为 磁焓 的热力学势导出：

其中，\mu_0 和 \mu_r 分别是自由空间和相对磁导率。磁通量矢量的分量, 必须在材料框架上取值，右柯西-格林变形张量为

\textup C=\textup F^{\textup T} \textup F，J=\textup{det}(\textup F)

和 \textup F=\nabla \textbf u + \textup I，其中，\textbf u 是位移场，\textup I 是单位张量。机械能函数 W_s(\textup C) 取决于使用的实体模型。

总第二类皮奥拉-基尔霍夫应力张量由下式给出

磁通密度矢量由下式计算

磁应力张量由下式计算

也就是所谓的 Minkowski 磁应力张量，它将被当作实体载荷施加到固体上。

对应的电磁体力可以写为

有时也被称为 Korteweg-Helmholtz 磁力，其中 \textbf J 是电流，\chi=\mu_r-1 是磁化率，它可以是材料中机械应变的函数。这表明体力包括洛伦兹力和来自磁极化的力贡献。感应电流效应被考虑包括在内，并且是在没有施加外部电流存在时，对洛伦兹力的唯一贡献量。

由周围磁场引起的边界应力 \sigma_{\textup E \textup M}^\textup{(out)} 被施加在表面，可以由下式计算

其中，\textbf H 和 p 是固体边界外侧的磁场和环境压力。

COMSOL Multiphysics 并未明确在耦合特征中包含环境压力定义。但是，如果压力已知或由另一个物理场接口（例如声学模型）计算，则可以向相应的 固体力学 接口添加额外的表面力。

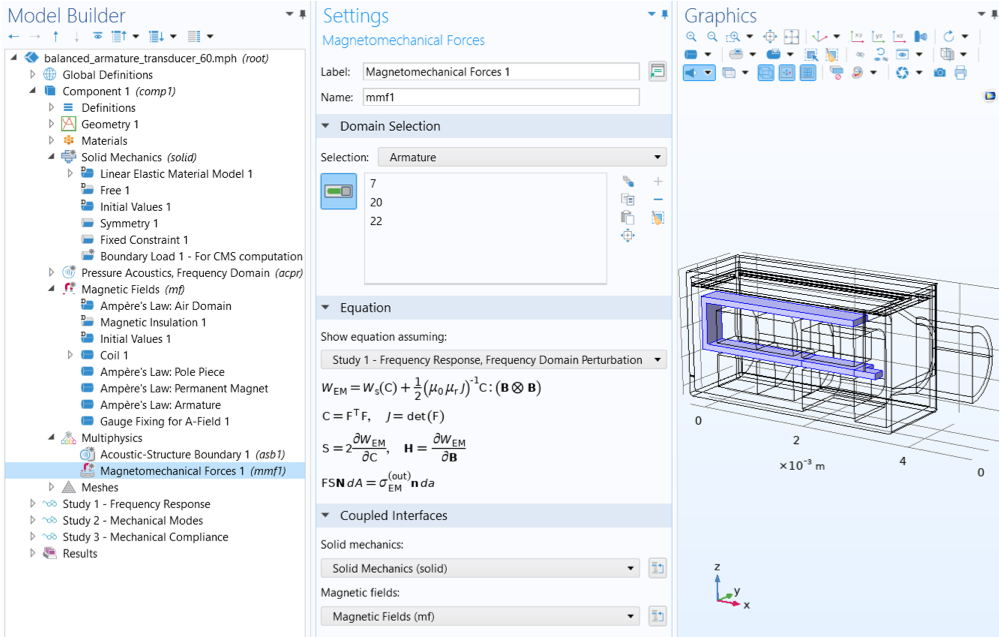
如下图所示，在平衡电枢传感器教程模型中，可以看到磁机械力耦合 特征的使用。

磁机械力耦合 特征用于平衡电枢传感器的完整振动电声仿真。

压电效应

压电驱动器的工作原理是压电效应，这是一种存在于某些被称为压电材料的晶体材料中的独特物理现象。直接压电效应包括当压电晶体变形时沿固定方向的电极化。极化与变形成正比，并在晶体上产生电位差。另一方面，逆压电效应与直接效应相反。它描述了施加电场时晶体中产生的变形，这是压电驱动器运行的原理。

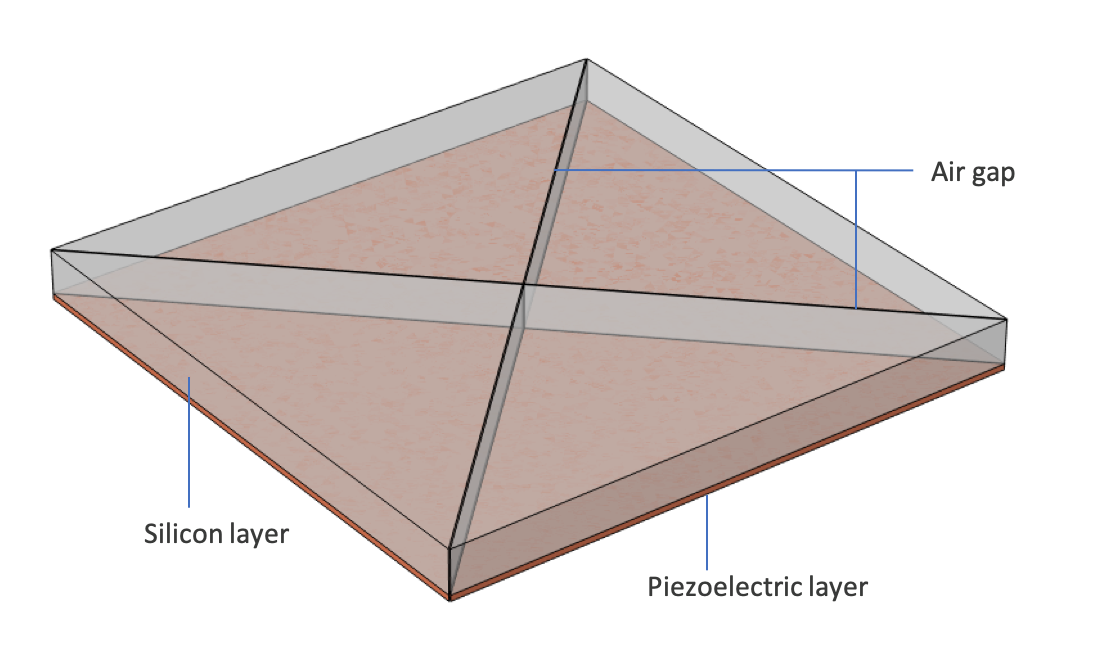
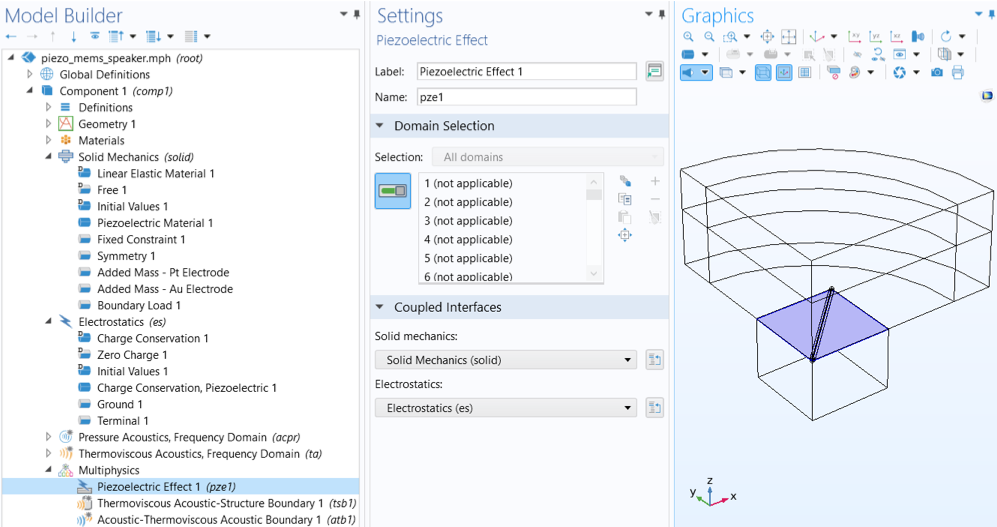
一种由四个三角形膜片组成的压电 MEMS 扬声器，利用压电效应产生振动。在厚度方向上应用较大的比例以进行可视化。

正向和逆向压电效应由 COMSOL 软件的静电 接口和固体力学 接口之间的多物理场耦合特征压电效应 捕获。每个物理场都包含一个专用的压电材料模型，在固体力学 接口中命名为压电材料，在静电 接口中命名为电荷守恒，压电，用于解释压电域中的特定本构关系。两个物理场中的两个压电材料模型通过压电效应 多物理场特性耦合。可以用应力-电荷形式或应变-电荷形式来表达应力、应变、电场和电位移场之间的关系。

压力电荷：

应变电荷：

其中，\epsilon 是应变，\sigma 是压力，\textbf E 是电场，\textbf D 是电位移场。材料参数 c_E 和 s_E 对应材料的弹性和柔顺性，e 和 d 是耦合属性，\epsilon_0 和 \epsilon_r 是自由空间和相对介电常数。

压电 MEMS 扬声器教程示例演示了如何使用压电效应 耦合特征对压电驱动器进行建模。

压电 MEMS 扬声器教程中使用了 压电效应 耦合特征。

当需要对来自压电驱动器的声辐射进行瞬态分析时，可以选择使用间断伽辽金（dG 或 dG-FEM）方法对压电设备的振动和流体中的波传播进行建模。在这种情况下，压电波，时域显式 多物理场接口用于对驱动器进行建模，它结合了弹性波，时域显式 接口和静电 接口以及压电效应，时域显式 多物理场耦合。间断伽辽金公式允许使用显式时间步进方法解决完全耦合的问题，因此提供了一种有效的替代方法，用于模拟相对于波长的远距离的声音生成和传播。在使用间断伽辽金方法模拟压电效应博客文章中，我们对此进行了解释，并在使用压电换能器的超声波流量计 案例教程中进行了演示。

机电力

虽然静电驱动器也在电场中工作，但它的振动源是带电体之间的麦克斯韦应力。这类驱动器中的隔膜是一种薄而平的导电材料，通常在其表面上提供恒定电荷。隔膜被夹在两个称为格栅 或定子 的导电片之间。当音频信号异相施加到格栅上时，在带电的振膜和两侧的格栅之间会产生静电力。一个格栅推动隔膜，另一个格栅则拉动隔膜，从而移动空气并产生声音。

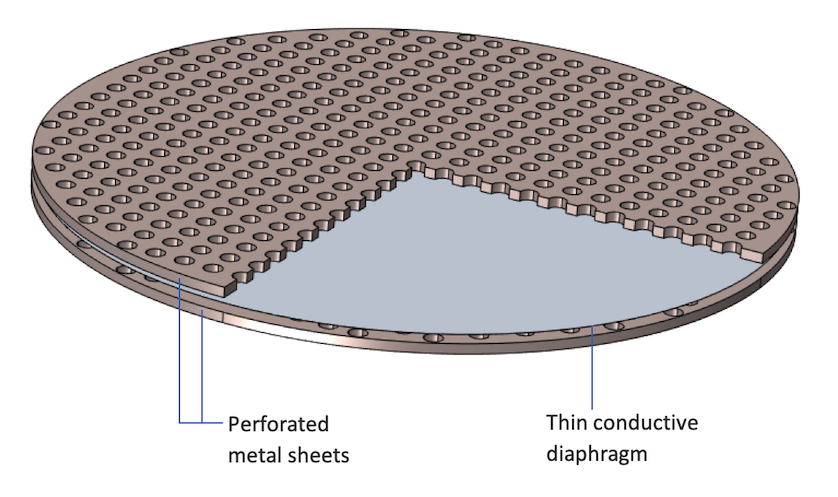
静电扬声器驱动器由位于两个穿孔金属板之间的薄塑料隔膜组成，利用带电体之间存在的麦克斯韦应力来触发振动。

这种类型的传感器可以使用机电力 耦合特征进行建模，这是静电 接口和固体力学 接口之间的另一种多物理场耦合。它计算带电体之间的介电力，以及结构变形对材料极化的影响。

磁机械力 耦合的理论非常相似，该力是在电场中而不是磁场中产生的。此外，还有两个贡献分量：在极化电介质体内产生并建模为体载荷的应力，以及由周围电场感应并作为边界载荷施加在表面上的应力。

对于有限变形，介电应力和材料极化的表达式可以使用下面被称为电动焓 的热力学势导出：

式中，\epsilon_0 和 \epsilon_r 是自由空间和相对介电常数。电场的组成部分 \textbf E, 必须在材料框架上取值，右柯西-格林变形张量为

\textup C=\textup F^{\textup T} \textup F, J=\textup{det}(\textup F)

\textup F=\nabla \textbf u + \textup I，其中，\textbf u 是位移场，\textup I 是恒等张量。机械能函数 W_s(\textup C) 取决于使用的实体模型。

总第二类皮奥拉-基尔霍夫应力张量由下式给出

电位移由下式计算

介电应力张量由下式计算

也就是所谓的 Minkowski 电应力张量，被施加在实体。

对应的电磁体力可以写为

有时，也被称为 Korteweg-Helmholtz 电力，其中 \rho_e 是电荷，\chi=\epsilon_r-1 是电磁化率，它可以是材料中机械应变的函数。

在表面上施加由周围电场引起的应力，可以由下列公式计算

其中，\textbf E 和 p 是固体边界外侧的电场和环境压力。

COMSOL Multiphysics 并未明确在耦合特征中包含环境压力定义。但是，如果压力已知或由另一个物理场接口（例如声学模型）计算，则可以向相应的固体力学 接口添加额外的表面力。

静电扬声器驱动器教程案例演示了如何使用机电力 耦合特征来模拟静电感应的振动。

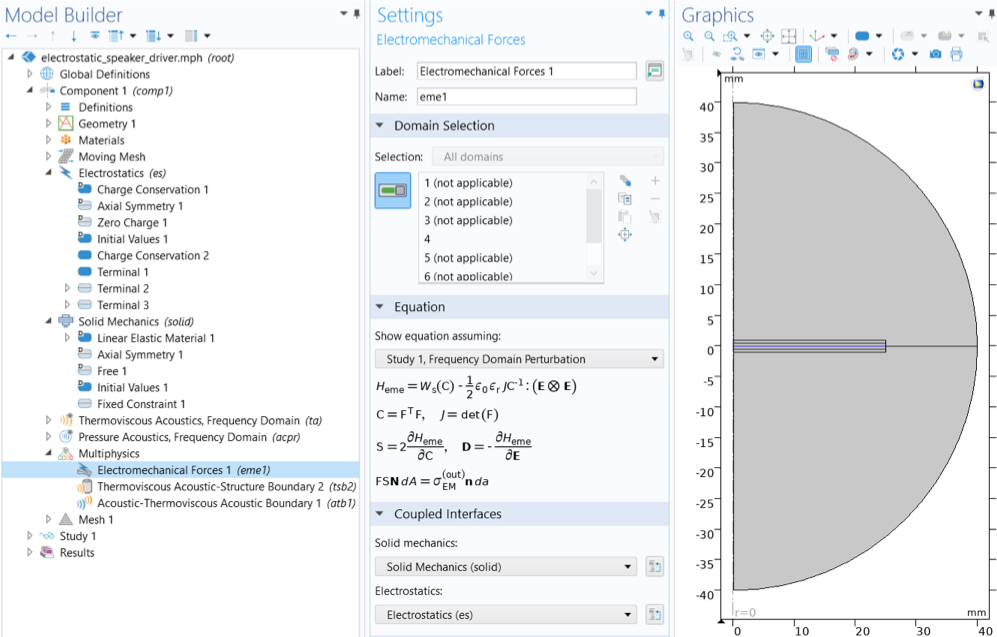
静电扬声器驱动器教程中使用机电力耦合特征来模拟静电驱动膜片的振动。

添加声学接口模拟声辐射

评估扬声器驱动器的性能通常需要分析对周围流体的声音辐射。在 COMSOL 中可以添加声学 接口并使用以下耦合特征将其耦合到固体振动模型：

• 声–结构边界：这个功能用于将压力声学模型耦合到任何结构组件。包括基于 FEM 的声学接口和基于 BEM 的声学接口。前面提到的案例教程，即扬声器驱动器-频域分析、扬声器驱动器-瞬态分析和平衡电枢传感器都是使用基于 FEM 的压力声学接口的示例。我们可以在敞开式扬声器教程模型中的看到将基于 BEM 的压力声学接口与结构振动耦合的示例。
• 声–结构边界，时域显式：这个特征专用于使用间断伽辽金法和时域显式求解器求解的瞬态声-结构相互作用问题。它与 压电效应、时域显式 耦合功能兼容，用于对来自压电扬声器驱动器的声辐射进行瞬态分析。有关演示，请参阅使用压电换能器的超声波流量计教程模型。
• 热黏性声–结构边界：这项功能用于将热黏性声学 接口与任何结构组件耦合。当黏性损失和热传导由于边界层的存在而变得重要时，需要热黏性声学模型来准确模拟狭窄流体通道中的声学。这在压电 MEMS 扬声器和静电扬声器驱动器教程模型中得到了例证。

三个耦合特征中的每一个都有一个对版本：对，声学–结构边界 耦合；对，声–结构边界，时域显式 耦合；对，热黏性声–结构边界 耦合。这些特征用于将声学接口耦合到已创建一致对的装配几何体中的固体力学 接口。这允许在声-结构边界使用非一致性网格。由于固体和流体中的波速不同，计算网格在解析波时可以利用这一点。通过这种方式，可以在求解时节省自由度。声–结构边界对，时域显式 耦合选项对于基于间断伽辽金法的模型特别有用，因为需要避免由于特定材料域中不必要的小网格单元导致的小内部求解器时间步长，如间断伽辽金法这篇博客文章中所述。

为大变形添加移动网格特征

在结构变形很大并且会显著影响电磁场（无论是电的还是磁的）的情况下，可以使用移动网格 特征来解释由于结构变形而导致的拓扑变化对电磁场分布的影响。这在静电扬声器驱动程序教程示例中进行了演示。

移动网格也可以用来捕获由于声场拓扑变化引起的非线性效应，该效应由具有大变形的扬声器振膜产生。扬声器驱动器-瞬态分析模型使用移动网格 特征和自动重新划分网格 来捕获拓扑变化和音圈的移动。

下一步

这篇博文讨论了 4 种 COMSOL 软件中可用的耦合特性，用于对市场上最常见的扬声器驱动器进行建模。点击下列链接进入 COMSOL 案例库，下载相应文档和 MPH 文件探索文中提到的模型：

• 扬声器驱动器—频域分析
• 扬声器驱动器-瞬态分析
• 平衡电枢传感器
• 压电 MEMS 扬声器
• 静电扬声器驱动器

如果你想了解访问这些耦合特征需要哪些模块，请联系我们。