“案例下载”页面提供丰富的 COMSOL Multiphysics® 教学案例和 App 演示文件,涉及电气、结构、声学、流体、传热和化工等各个学科领域。欢迎下载这些教学案例或 App 演示文件及其随附的操作说明,将其作为您建模仿真工作的绝佳起点。
您可以使用左侧的【快速搜索】工具查找与您的专业领域相关的案例模型和仿真 App。请注意,此处提供的许多案例也可以通过 COMSOL Multiphysics® 软件内置的“案例库”进行访问,该选项位于软件的文件 菜单中。
中文 带有此标签的案例包含中文 PDF 文档。
本教学案例基于 B. J. Baliga 编写的 "Fundamentals of Power Semiconductor Devices" 一书(2008 年版,第 242 页),模拟一个简单 PIN ... 扩展阅读
这个教学案例求解由简谐势阱束缚的旋转玻色-爱因斯坦凝聚体中涡格形成的 Gross–Pitaevskii 方程,这本质上是一个非线性单粒子薛定谔方程,粒子间的相互作用通过与局部粒子密度成比例的势能贡献表示 ... 扩展阅读
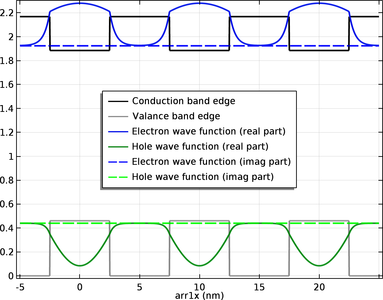
“超晶格带隙工具”模型有助于设计由两种交替半导体材料(超晶格)构成的周期性结构。此模型采用有效质量薛定谔方程来估计给定超晶格结构中的电子和空穴基态能级。器件工程技术人员可以使用此模型快速计算给定周期结构的有效带隙 ... 扩展阅读
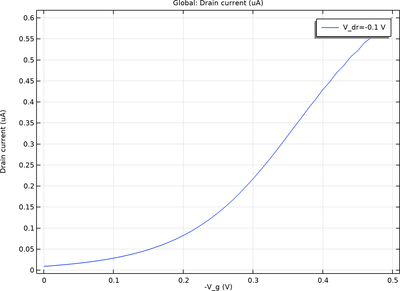
本例演示如何在三维空间中对 FinFET 进行建模仿真,以获取其电流-电压 (I-V) 特性。首先,通过扫描栅极电压,绘制出漏极电流与栅极电压的关系曲线。随后,在固定栅极电压条件下,进一步计算漏极电流随漏极电压变化的特性。 扩展阅读
本模型演示如何基于一般的漂移-扩散模型来模拟电解质栅极有机场效应晶体管,其中使用“稳定对流-扩散方程”和“静电”接口,并显示晶体管特性的可视化效果。所模拟器件中 EDL 的形成过程展示了 EGOFET 的关键特性。 扩展阅读
在 MESFET 中,栅极形成整流结,该整流结通过改变结的耗尽宽度来控制沟道的开口。 在此模型中,我们模拟了 n 掺杂砷化镓 MESFET 对不同漏极和栅压的响应。对于 n 型掺杂材料 ... 扩展阅读
在这个由两部分组成的示例的前半部分,我们构建一个沟槽栅 IGBT 二维模型,然后在后半部分将其扩展成三维模型。通常,最有效的方法是从二维模型开始,以确保一切按预期工作,然后再将其扩展到三维。本例将 Caughey ... 扩展阅读
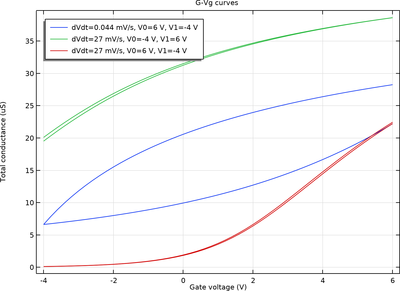
本教程分析 InAs 纳米线 FET 的电导-栅极-电压 (G-Vg) 曲线的滞回现象,使用密度梯度理论将量子限域效应添加到传统的漂移-扩散公式中,不会大幅增加计算成本。这种滞后现象是由连续能量分布 ... 扩展阅读
本模型演示如何模拟碳化硅二极管中由碰撞电离引起的雪崩击穿,呈现了器件的电流-电压 (I-V) 特性及电场分布图。此外,还计算了载流子产生项,以展示击穿电流的路径。 扩展阅读