问题描述
我正在求解一个瞬态模型,并期望解随时间产生振荡,以响应载荷的阶跃变化。如何建立这样的模型?应该对求解器做哪些更改?
解决方法
在涉及时变载荷响应的某些模型中,会产生随时间变化的波型解或振荡解。常见的例子包括瞬态压力声学公式和瞬态电磁波公式。控制方程是双曲型偏微分方程,对应的解分别表示声波和电磁波。在使用“结构力学”接口进行时域分析时,也会产生振荡解。比如一个张紧的吉他弦问题:当弦被突然拨动时,它将以基频振动,并产生大量较高的泛音。
鉴于 COMSOL 瞬态求解器选择时步来计算解的原理,无论求解哪个物理场,我们都需要稍微分析一下所有这类模型中载荷的施加方式。默认情况下,软件会自动调整时间步长以捕获(在指定容差内)系统响应。如果外加载荷发生瞬时变化,这可能会导致时步非常小。
比如,我们分析一个时变载荷(如下所示)及其“傅里叶变换”。载荷瞬时变化,从而产生大量高频部分。虽然这些高频分量的幅度确实在减小,但它们仍然很明显。如果我们用这种载荷来激励结构,软件会尝试解析所有这些高频部分,并开始采用非常小的时步(与周期的一小部分成正比)来计算系统响应。

时变阶跃载荷及其傅里叶变换
然而,从建模的角度来看,我们实际上并不需要分析所有这些高频部分(解中较高的泛音和小振动等)。解决方法是对输入信号进行平滑,以避免任何突变。由于大部分载荷实际上不会发生瞬时变化,因此,从物理上来说,这样做是可行的。从建模的角度来看这也是合理的:高频部分包含系统总能量的一小部分,并且没有多少实际意义。下图中的红色部分显示这种平滑输入信号及其“傅里叶变换”的一个例子。请注意,信号的低频部分几乎没有变化,但与原始信号相比,经平滑处理的信号在某一点之后包含的较高频率部分可以忽略不计。
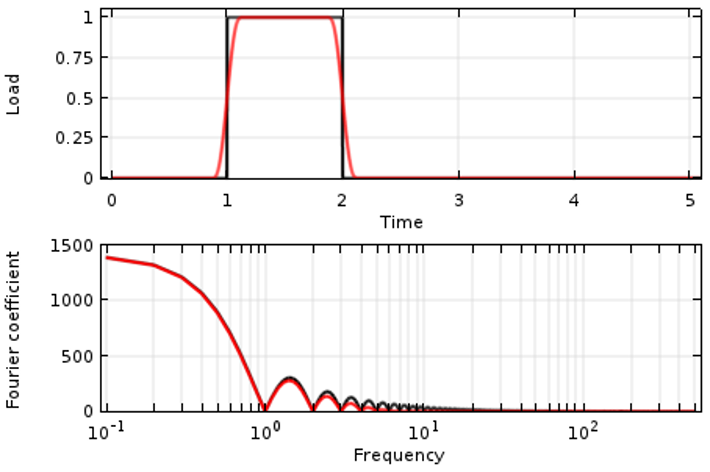
平滑后的时变阶跃载荷(红色曲线)及其傅里叶变换。
内置的方波、三角波、阶跃、斜坡以及类型为锯齿波、方波和三角波的波形都包含信号平滑选项,如下图所示。分段函数还支持在区间之间进行平滑处理。如果您要设置其他类型的用户定义载荷,请确保也对其进行某种平滑处理。有关更多信息,请参阅 COMSOL Multiphysics Reference Manual > Global and Local Definitions > Functions > Specifying Discontinuous Functions > Additional Smoothed Functions。
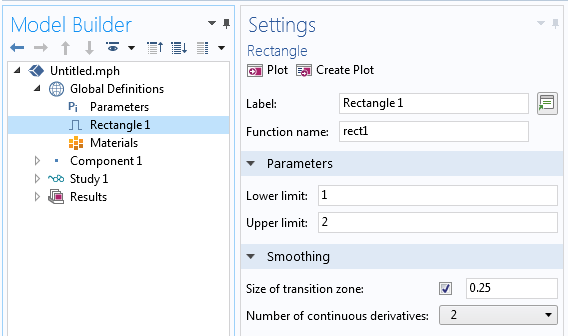
对内置函数进行平滑。
在对所有加载的函数进行适当的平滑处理后,您还将了解激励的最大可能频率组成。您可以据此选择合适的网格,然后手动调整时步,如知识库 1118:解析瞬态波中所述。
另请参见:
COMSOL 尽一切合理的努力验证您在此页面上查看的信息。本页面提供的资源和文档仅供参考,COMSOL 对其有效性不作任何明示或暗示的声明。COMSOL 对所披露数据的准确性不承担任何法律责任。本文档中引用的任何商标均为其各自所有者的财产。有关完整的商标详细信息,请参阅产品手册。



