Modeling with Partial Differential Equations in COMSOL Multiphysics®
This 11-part, self-paced course is an introduction to modeling with partial differential equations (PDEs) in COMSOL Multiphysics®. Through comprehensive, step-by-step demonstrations in the COMSOL® software, you will learn how to implement and solve your own differential equations, including PDEs, systems of PDEs, and systems of ordinary differential equations (ODEs). Model files are included in each part of the course, so you can follow along at your own pace. Because of this, this course is useful for anyone who is just getting started in the software as well as for experienced users who want to expand their skill set with equation-based modeling. The examples span a wide range of physics and mathematics and include models for electromagnetics, structural mechanics, acoustics, chemical engineering, and fluid flow. Although there are easy-to-use, built-in physics interfaces for nearly all the examples illustrated in this course, learning how to implement the corresponding equations using the equation-based interfaces in COMSOL Multiphysics® can be useful for a number of reasons. For instance, you can:
- Gain the necessary skills for implementing your own custom equations
- Extend and modify the functionality of the built-in physics interfaces
- Gain a deeper understanding of the inner workings of the software
Furthermore, for educational purposes, COMSOL Multiphysics® is an excellent software for learning about partial differential equations through hands-on experience.
This course will not cover all of the basics of PDEs and their meaning and applications, but rather how to use COMSOL Multiphysics® for modeling with PDEs. If you think you need a refresher on mathematical modeling with PDEs in general, please review the cyclopedia article on "Physics, PDEs, Mathematical and Numerical Modeling".
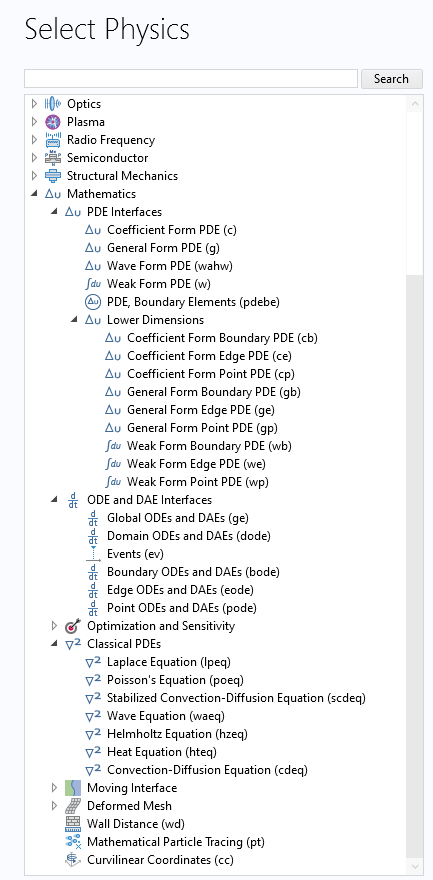
The Model Wizard, where the mathematics interface options for PDE modeling are expanded.
An overview of the topics covered throughout the course are as follows:
Part 1: Poisson's and Laplace Equations
- Getting started with the mathematics interfaces for modeling with partial differential equations
- Setting up your first equation
- Solving using both the finite element method and the boundary element method
- Defining your own field quantities and examining the results
Part 2: Diffusion-Type Equations
- Modeling classical PDEs
- Using the Coefficient Form PDE interface and General Form PDE interface
- The terminology for PDE coefficients
- Understanding boundary conditions
- The user interface syntax for equation-based modeling
Part 3: Convection–Diffusion Equations
- The continuity equation
- Convective and diffusive flux
- Using the Coefficient Form PDE interface for solving convection–diffusion equations
- Numerical stabilization
- Nonlinear equations
Part 4: Coordinate Transformations
- Transforming PDEs using cylindrical coordinates
- Axially symmetric modeling of convection-diffusion-reaction PDEs
- Using the Coefficient Form PDE and General Form PDE interfaces for analyzing a chemical reactor
Part 5: Using the Interfaces for Lower Dimensions, ODEs, and DAEs
- The PDE interfaces for modeling in lower dimensions
- Using the Coefficient Form Boundary PDE interface
- Implementing the equations for electric currents in a shell
- Coupling PDEs of different dimensions
- Modeling distributed ODEs and differential algebraic equations (DAEs)
- Modeling algebraic equations
Part 6: Global ODEs and DAEs Interface
- The Global Equations interface for modeling ODEs
- Initial value problems
- Linear scalar ODEs
- Linear systems of ODEs
- Nonlinear systems of ODEs
- Chaotic systems of equations
- DAEs
- Coupling of PDEs and ODEs
Part 7: Helmholtz Equation
- The wave equation and Helmholtz equation
- Plane wave solutions
- Radiation boundary conditions
- Complex-valued quantities
- Techniques for meshing and solving Helmholtz equation models
Part 8: Multiphysics Systems of Equations
- Modeling with multiple dependent variables
- Implementing Joule heating using PDE interfaces
- Defining your own units
Part 9: Vector- and Tensor-Valued Systems of Equations
- Formulating structural mechanics using PDEs
- Implementing plane stress using the Coefficient Form PDE interface
- Comparing results from custom equations with built-in equations
Part 10: Using the Weak Form for Scalar Equations
- Energy minimization problems
- Variational calculus
- Understanding the weak form of a PDE
- Implementing the equations for electrostatics and electric currents using the weak form
- Point charges and point sources
Part 11: Using the Weak Form for Equation Systems
- The weak form of the equations of linear elasticity
- Implementing plane stress using the weak form
- The Equation View window
- The weak form for more general physics
- Different ways of using the Weak Form PDE interface
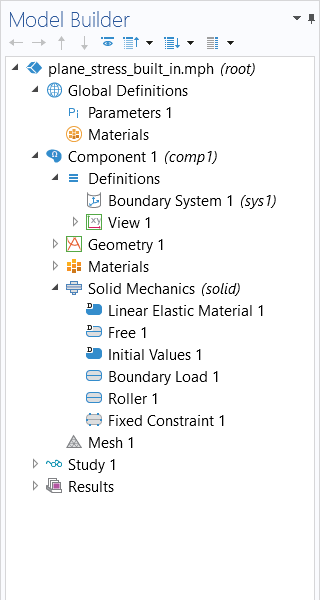
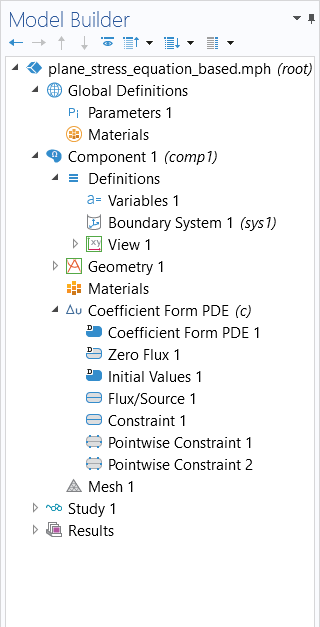
The model tree for an example built in Part 9 of the course, showing the model setup using the predefined physics interface (left) and the equation-based model setup (right).
After completing the course, you will have a thorough understanding of the workflow for modeling with partial differential equations in the software and have confidence in setting up your own custom system of equations.
请提交与此页面相关的反馈,或点击此处联系技术支持。












