
积分是数学模型中最重要的功能之一,特别是对数值仿真而言。例如,偏微分方程组 (PDEs) 就是由积分平衡方程派生而来。当需要对偏微分方程进行数值求解时,积分也将发挥非常重要的作用。本篇博客介绍了 COMSOL 软件中可用的积分方法,以及如何使用,供您参考。
积分的重要性
COMSOL 使用了有限元方法,它将控制 PDE 转化为积分方程,换言之,就是弱形式。如果仔细观察一下 COMSOL 仿真软件,您可能会发现许多边界条件都是由积分公式表示,例如总热通量或悬浮电位。积分在后处理中也非常重要,因为 COMSOL 提供了许多基于积分的派生值,比如电能、流速或总热通量。当然,用户还可以根据自己的方法来使用积分,在本篇博客中,我们将具体介绍如何实现。
利用派生值求积分
积分的一般形式如下:
其中,[t_0,t_1] 是时间间隔、\Omega 是一个空间域,而 F(u) 则是因变量 u 的任意一个表达式。 表达式可以包括相对空间与时间的派生值,或任何其他派生值。
通过功能区(在非 Windows® 操作系统中则为‘模型开发器’)‘结果’部分的“派生值”,可以最便捷地访问积分选项。
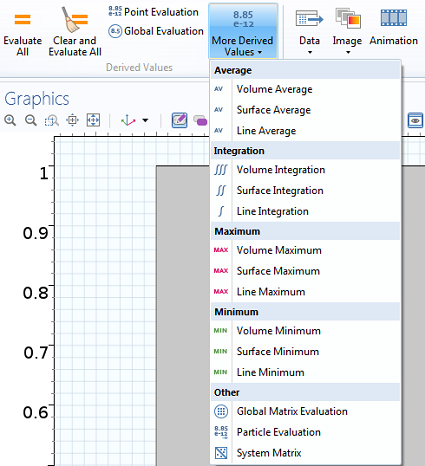
如何将体、面或线积分增加作为派生值。
您可以通过选定对应的数据集来引用任何可用的解。表达式框为被积函数,并支持因变量或派生变量。在瞬态仿真中,会计算每一个时间步长的空间积分。或者,设定窗口提供了‘数据系列操作’,可在此为时域选择积分选项。这将得到空间和时间的积分。
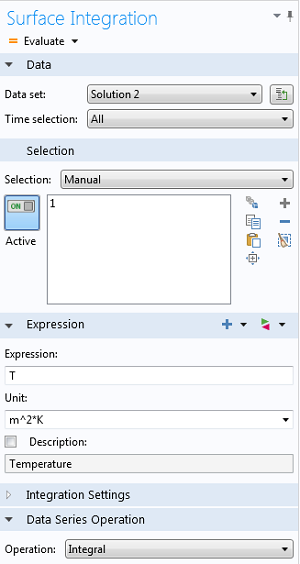
面积分设定示例,并通过‘数据系列操作’增加了额外的时间积分。
平均是另一个与积分相关的派生值。它等于积分结果除以所考察域的体积、面积或长度。平均中的‘数据系列操作’还可以将结果除以时间范围。派生值非常有用,但由于它们仅能用于后处理,所以无法处理所有的积分类型;因此 COMSOL还提供了更加强大和灵活的积分工具。我们将通过下方的模型示例演示这些方法。
传热示例模型中的空间和时间积分
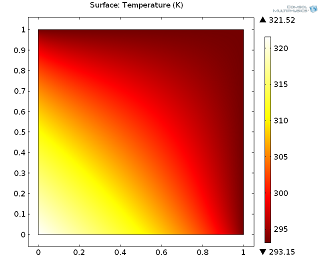
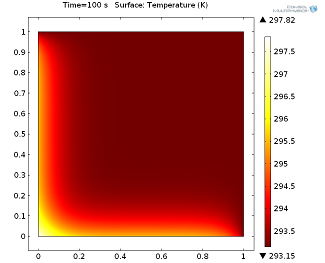
我们将介绍一个简单的传热模型,即 (x, y) 二维平面内的单位正方形铝。上侧和右侧固定为室温 (293.15 K),左侧和下侧规定有 5000W/m^2 的‘广义流入热通量’。下图显示了 100 s 后的稳态解和瞬态解。
利用组件耦合算子求空间积分
举例来说,当一个表达式中综合了几个积分,或在计算中需要积分,或需要一组路径积分时,就需要组件耦合算子。可以在对应组件的定义部分中定义组件耦合算子。在这个阶段,我们尚未计算这些算子,只是确定了它们的名称和对象选择。
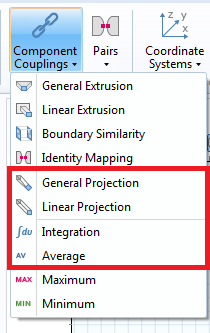
如何增加组件耦合算子方便后续使用。
在示例中,我们首先希望计算恒定温度下的空间积分,这可以通过以下公式计算:
在 COMSOL 软件中,我们使用了一个缺省名称为 intop1 的积分算子。
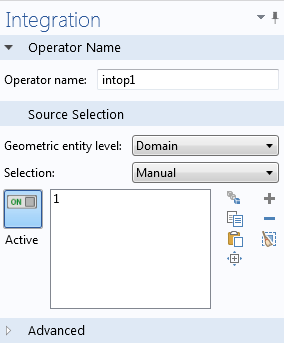
积分算子设定窗口。
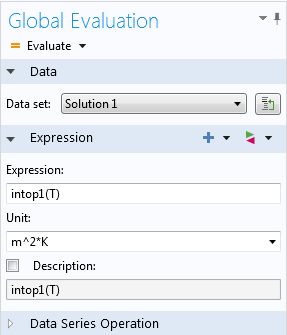
如何计算积分算子。
下一步,我们将演示如何在模型中使用积分算子。例如,我们希望计算将平均温度相对室温上升 10 K,即达到 303.15 K,需要施加多少热能。首先,我们需要计算目标温度与实际平均温度之差。平均温度可通过对 T 的积分除以对 1 的积分得到,对常数 1 的积分可以得到域的面积。幸运的是,在 COMSOL 中这类计算可以轻松地通过缺省名称为 aveop1 的平均算子得到。(注意域内的平均与我们的积分示例相同,因为域为单位面积。) 对应的温差可通过如下公式计算:
接下来,我们需要找到左侧和下方边界的‘广义热通量’,以便满足所需的平均温度。为此,我们增加了一个名为 q_hot 的额外自由度,以及一个额外的约束作为全局方程。将‘广义流入热通量’替换为 q_hot。

如何通过增加一个额外的自由度以及一个全局方程来把平均温度强制设为 303.15 K。
对这个耦合系统进行稳态求解,得到 q_{hot}=5881.30 W/m^2。要在整个域中得到 303.15 K 的平均温度,‘广义流入热通量’边界条件就应为这样的一个值。
利用积分耦合计算不定积分
我们的 Support 邮箱经常收到这样一个问题:如何得到空间不定积分?下面这个积分耦合的应用就将回答这一问题。不定积分与积分对应,从几何上讲,它支持计算由函数图形约束的任意面积。它的一个重要应用就是计算统计分析中的概率。为演示这一点,我们的示例固定为 y=0,并通过 u(x) 表示不定积分 T(x,0)。这意味着 \frac{\partial u}{\partial x}=T(x,0)。以下积分代表了该不定积分:
其中,我们使用 \bar x 来区分积分与输出变量。和上文的积分相反,我们这里将函数作为结果,而非标量。我们需要加入这一信息,即对于每个 \bar x\in[0,1],对应的 u(\bar x) 值需要求解一个积分。幸运的是,这在 COMSOL 环境中很容易设定,可以说,只需要三个组分。第一步,可以使用一个逻辑表达式将积分转化为:
第二步,我们需要一个积分算子作用在我们示例域的下边界。我们通过 intop2 来表示。第三步,我们需要加入积分与输出变量的区分。这一情况下源项与目标端的符号分别为 x 和 \bar x。当使用积分耦合算子时,内置算子 dest 可用,它指出对应的表达式不属于积分变量。更精确地说,它意味着 COMSOL 中的 \bar x=dest(x)。综合逻辑表达式与 dest 算子,得到表达式 T*(x<=dest(x)),这正是 intop2 所需输入的表达式。总之,我们可以通过 intop2(T*(x<=dest(x))) 计算不定积分,并在我们的示例中得到如下图示:
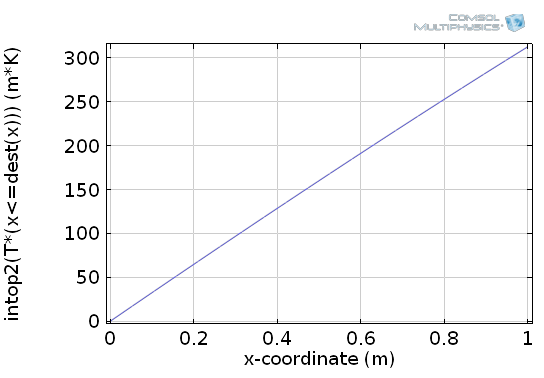
如何通过积分耦合、dest 算子,以及逻辑表达式绘制不定积分。
COMSOL 提供了两个不同的积分耦合算子,名称是广义投影和线性投影。可通过它们得到域任意方向的一组路径积分,即仅针对一个维度执行积分,结果是一个维度而非域的函数。在二维示例中,结果是一个一维函数,可以在任意边界进行计算。在接下来的一篇有关组件耦合的博客中,我们将更加详细地介绍如何使用这些算子。
在附加物理场接口求解空间积分
要最灵活地使用空间积分,可以将它增加到一个附加的 PDE 接口上。继续使用不定积分的例子,假设我们并非只希望计算 y=0 的不定积分。这一任务可以通过 PDE 阐释:
并在左边界上指定狄氏边界条件 u=0。系数型偏微分方程接口是执行这一方程的最简单接口,我们仅需作如下设定:

如何针对空间积分使用附加物理场接口。
因变量 u 代表相对于 x 的不定积分,在计算和后处理时可用。这种方法除了灵活性,还具有准确性的优势,因为积分并非作为派生值获取,而是作为计算及内部误差估计的一部分。
利用内建算子求时间积分
我们之前提到过‘数据系列操作’可以作为时间积分使用。通过分别代表了时间积分或时均的内置算子 timeint 和 timeavg 是实现时间积分另一项重要方法。它们可用于后处理中,能够对指定时间间隔的任何瞬态表达式执行积分操作。在示例中,我们对 90 s 和 100 s 的平均温度感兴趣,即:
下方的表面图显示了得到的积分,它是 (x,y) 中的一个空间方程。
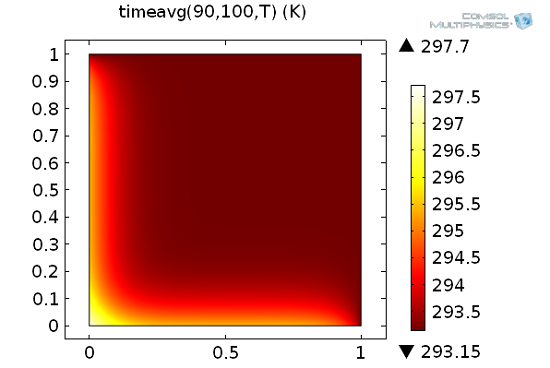
如何使用内置时间积分算子 timeavg。
类似的算子还有用于球面对象的积分,也就是 ballint、circint、diskint 以及 sphint。
利用其它物理场接口实现的时间积分
如果模型中要用到时间积分,您需要将其定义为额外的因变量。与上方显示的系数型偏微分方程示例类似,这可以通过增加数学分支的常微分方程接口实现。例如,假设在每个时间步长,模型均需要从开始时刻到当前的总热通量,即需要测量累计能量。COMSOL 会自动计算总热通量变量,名称为 ht.tfluxMag。积分可以作为带有分布式常微分方程的附加因变量计算,它是域常微分和微分代数方程 接口的子节点。该域常微分方程的源项为被积函数,如下图所示。
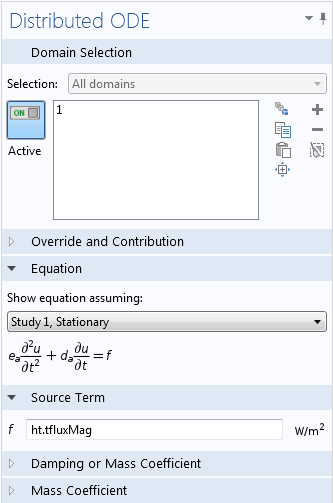
如何针对时间积分使用附加的物理场接口。
这类计算的优势是什么呢?积分可以在另一个物理场接口重复使用,比如那些可能会被系统中的累计能量影响的接口。此外,它现在还可用于各类后处理,比内建算子更加便捷和高效。例如,检查多相催化模型中的碳沉积,模型使用域常微分方程来计算催化剂的孔隙率,并以此作为存在化学反应时的瞬态场变量。
求解析函数及表达式的积分
到目前为止,我们已经显示了如何在计算或后处理中求解变量的积分,但我们尚未涉及到解析函数或表达式的积分。为此,COMSOL 还提供了内置算子 integrate (表达式、积分变量、下边界,及上边界)。
表达式可能是任意一维函数,例如 sin(x);也可能包括附加变量,例如 sin(x*y)。第二个参数指出了对哪个变量求积分。例如利用 integrate(sin(x*y),y,0,1) 可以得到一个有关 x 的函数,因为积分仅会消除积分变量 y。积分算子也可用于处理解析函数,我们需要在当前组件的定义节点定义解析函数。
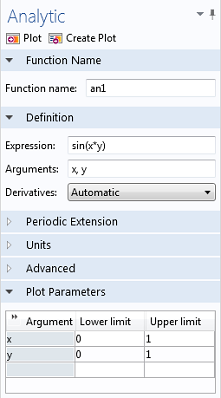
如何增加一个解析函数。
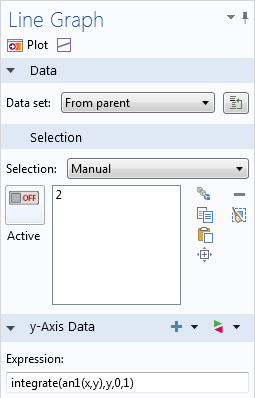
如何求解析函数的积分。
扩展阅读
- 模型下载
- 使用积分耦合算子:汽车消音器
- 使用时间积分的全局方程:PID 控制器的过程控制
- 使用全局方程来满足约束:使用全局方程满足约束条件
- 使用时间积分的域常微分方程组:锂离子电池的容量衰减 与 多相催化中的碳沉积





评论 (22)
高 永潘
2016-08-16为此,我们增加了一个名为 q_hot 的额外自由度,以及一个额外的约束作为全局方程。将‘广义流入热通量’替换为 q_hot。 这里为什么q_hot是一个广义的热通量。它是这么通过这个全局约束方程实现的?能否给予下解释。在这里先谢谢
高 永潘
2016-08-16为此,我们增加了一个名为 q_hot 的额外自由度,以及一个额外的约束作为全局方程。将‘广义流入热通量’替换为 q_hot。数学上为什么这样的约束会使系统q_hot 对应一个广义热通量?
Lei Zhang
2016-11-22看完这篇博客,有很大收获,有一个疑问假如我需要对空间电流密度积分(积分函数为j/r),然后赋值到对应的边界上,请问这个在comsol怎么实现?谢谢!
kai zhang
2016-11-24@高永潘:这是根据建模的目的决定的,该模型希望得到在指定平均温度下的流入热量大小,可通过热通量中的广义热通量来描述(单位W/m^2), 全局ODE可以理解为一种映射关系,指定q_hot的大小满足aveop1(T)=303.15K. 也可参考该案例中的设置:http://cn.comsol.com/model/flexible-and-smooth-strip-footing-on-stratum-of-clay-2203
kai zhang
2016-11-24@高永潘: 此处的q_hot是任意写得一个名称,只有在广义热通量条件中输入该名称即可。此处ODE的意义可以理解为一种对应关系,相当于在原来的方程上添加一个一个常微分方程约束条件,q_hot的数值满足Aveop1(T)=303.15。也可参考该案例:
http://cn.comsol.com/model/flexible-and-smooth-strip-footing-on-stratum-of-clay-2203
kai zhang
2016-11-24test
Yuansheng Zheng
2016-11-25@leizhang: 要看边界数值是否取均匀数值,如果为均匀实在,则直接定义一个‘变量’为电流密度的积分,然后在边界条件中输入该变量即可。如果边界上所取数值与积分位置有关(边界每一个点上的数值都取此处沿边界面法向的线积分进行投影),则会比较麻烦,需要用到定义-组件耦合-广义投影操作实现,具体请参考基本模块用户手册reference manual
海轩 诸葛
2016-12-27在2D模型中,怎样对一个随机加速度进行积分了?
宇航 秦
2016-12-28@诸葛海轩:
您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
lei jin
2017-02-12lei jin
2017-02-12你好 在案例:heat_sink_CN.mph – 2.76MB 中,我想设置一个全局ODE来求得速度V满足芯片平均温度等于一个值但是一直实现不了,而约束热流量来使平均温度等于一个值就可以。请问关于全局约束方程更具体一些的介绍吗?
宇航 秦
2017-02-13@lei ji:
您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
peng liu
2017-09-27您好,请问我想利用派生值计算光通过硅表面时在各个波长下的反射和透射率,我该选择什么计算方式呢?或者有没有相关的案例可以让我学习一下。谢谢,盼复。
peng liu
2017-09-27您好,我想利用派生值计算光通过硅表面时,随各个波长变化的反射和透射率,我该选择哪种计算方式呢?或者有没有相关的案例可以让我学习一下?谢谢
宇航 秦
2017-11-06Liu Peng,
您好!
感谢您的评论。
模型相关的问题,请您联系我们的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!
超 程
2018-11-27定义了全局方程之后,我将q_hot放在右边界和上边界,而左边界又边界的热源依旧是5000,是否可以得到当右上环境温度为q_hot[K]时,平均温度达到303.15K时的一个q_hot?可是如此得到的结果,q_hot=10295,aveop1(T)=10303,与实际结果严重不符。请问是什么原因造成了这样的情况?非常感谢您的耐心回答!
华韶 廖
2018-12-17您好 ,我想问一下,多个 pde之间是如何耦合的,需要什么条件呢?谢谢
CHGAOBIN REN
2019-03-27盼 彭
2021-04-19官方能不能讲下后处理中派生值下的小节点,像线积分、最大值具体怎样操作,你在录制视频时候一笔带过,这是要专门培训吗?
hao huang
2021-04-22 COMSOL 员工您好,目前已将您的建议反馈给技术部门。
Zheng He
2023-09-22请问在组件下定义积分与结果派升值中定义积分的区别是什么?
Qihang Lin
2023-09-25 COMSOL 员工组件下定义积分随运算运行一并计算,后处理派生值中定义的积分是计算完之后对数据集中的结果进行积分。