基于方程建模 博客文章

捕蚊器真的有用吗?通过粒子追踪法预测捕蚊器的性能
2023年 10月 12日
你是一个蚊子吸引者吗?让我们用基于方程的建模来模拟一个有趣的场景,探索蚊子是喜欢捕蚊器还是喜欢人的皮肤。

使用 COMSOL® 进行衍生式设计以获得新灵感
2021年 11月 2日
一个新的设计是源自人还是过程?我们可以想象一个新设计的产生过程:首先设计师先有一个设想,然后拿起铅笔把他的想法变成现实。当然,今天的设计师和工程师可能不使用铅笔,也可能没有一个最终的设计想法。

为什么高尔夫球有凹痕?
2021年 10月 1日
高尔夫球为什么会有凹痕?我可以用 COMSOL Multiphysics 模拟高尔夫球吗?我可以使用仿真来优化我的击球并打出标准杆吗?下面带大家找出这些问题的答案。

使用 COMSOL Multiphysics® 进行微磁仿真
2021年 9月 24日
中国复旦大学的余伟超博士使用 COMSOL Multiphysics® 中的“物理场开发期”创建了一个“微磁模块”,用于执行微磁模拟。
如何使用 COMSOL® 模拟代谢反应网络
2021年 8月 4日
某些冰淇淋、布丁和糖果具有非常鲜艳的黄色,这种黄色来自维生素 B2。 该补充剂的制造是代谢反应网络的一个例子……

将自适应网格细化与数据过滤相结合
2021年 3月 19日
在我们之前关于数据过滤的博客文章的后续文章中,我们演示了如何为具有非均匀热负载的热模型实现自适应网格细化和亥姆霍兹滤波器。
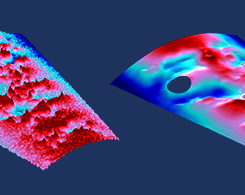
使用数据过滤提高模型性能
2021年 3月 17日
想要在您的模型中包含实验数据作为负载或边界条件,但数据随空间或时间变化并且有噪声? 尝试实现数据过滤,例如亥姆霍兹过滤器。

将全局方程引入全耦合目标搜索法
2021年 1月 20日
今天,我们将在 COMSOL Multiphysics® 软件的模型中引入一个目标搜索方程,该方程与全耦合方法结合使用可以求解非线性问题。在计算上,尽管这种方法比我们之前介绍的分离式求解方法成本更高,但其在鲁棒性方面却具有一些独特的优势,并能够突显 COMSOL® 软件的一个核心优势。
