“案例下载”页面提供丰富的 COMSOL Multiphysics® 教学案例和 App 演示文件,涉及电气、结构、声学、流体、传热和化工等各个学科领域。欢迎下载这些教学案例或 App 演示文件及其随附的操作说明,将其作为您建模仿真工作的绝佳起点。
您可以使用左侧的【快速搜索】工具查找与您的专业领域相关的案例模型和仿真 App。请注意,此处提供的许多案例也可以通过 COMSOL Multiphysics® 软件内置的“案例库”进行访问,该选项位于软件的文件 菜单中。
中文 带有此标签的案例包含中文 PDF 文档。
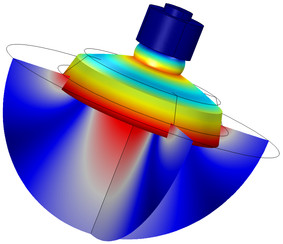
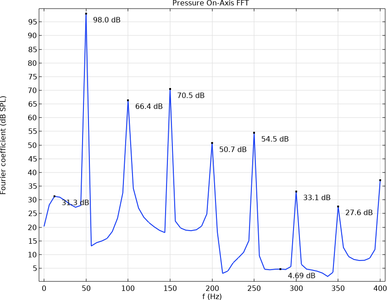
Tonpilz 型(蘑菇形)压电换能器是用于频率相对较低的大功率声发射的换能器。换能器由压电陶瓷环组成,这些压电陶瓷环堆叠在两个质量块之间,由中心螺栓预加应力。尾部和头部质量块可降低装置的谐振频率。 ... 扩展阅读
超材料中的模式色散可以通过改变组成基本单元的材料类型和尺寸来进行设计。例如,周期性排列的亚波长金属-介质多层超材料在矩量空间中表现出各向异性的色散特性。在特定频率范围内,这种结构的介电常数会在正交光轴上呈现相反的符号 ... 扩展阅读
本教学案例演示如何对导入的 CAD 几何执行虚拟几何操作。这些虚拟操作,如形成复合实体或忽略实体,有助于提高网格质量,减少单元总数。 扩展阅读
本模型演示如何在简化的扬声器分析中包含某些集总元件的非线性(大信号)特性,并使用等效电路对机械和电气系统进行建模,其中的大信号柔度 CMS(x) 和力因子 BL(x) 是扬声器位置的非线性函数。此外,机械阻尼 RMS ... 扩展阅读
灵敏度分析是一种计算目标函数相对于多个控制变量的梯度的有效方法。 本例采用桁架塔顶部的俯仰和偏转作为目标函数,计算这些角度相对于各个桁架构件直径变化的灵敏度。 扩展阅读
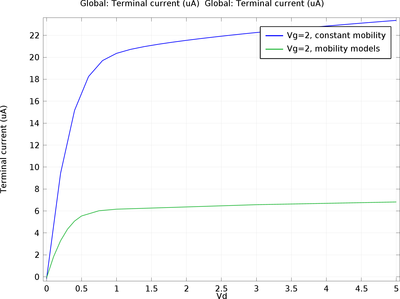
本模型展示了如何在已有的简单 MOSFET 案例模型中,添加多个链接的迁移率模型。 扩展阅读
模型提取硅 p-n 结二极管的 SPICE 参数,用于创建半波整流器的集总元件等效电路模型。将模型与完整器件仿真进行了比较。在示例中,将二维网状 p-n 结二极管连接到包含正弦源、电阻器和接地的电路 ... 扩展阅读
本教学案例演示在设计毫米波应用中常用的接地共面波导 (GCPW) 电路时,如何在物理场接口中设置端口特征。 扩展阅读
屈曲是细长结构组件的常见故障模式。该模型在约束斜撑体积的同时,最大限度地提高了斜撑的屈曲载荷。 扩展阅读