
从 COMSOL Multiphysics® 软件 6.0 版本开始,我们在半导体模块中对半导体 物理场接口的金属接触 边界条件引入了可选的接触电阻的贡献,也就是能够设置金属电极接触材料的电阻。在这篇博文中,我们将使用跨桥开尔文电阻器的基准模型来讨论如何应用这个新功能。
模型结构
跨桥开尔文电阻器结构通常用于表征金属-半导体接触的接触电阻。本文,我们选用了参考文献1中描述的一系列特定测试结构进行研究。
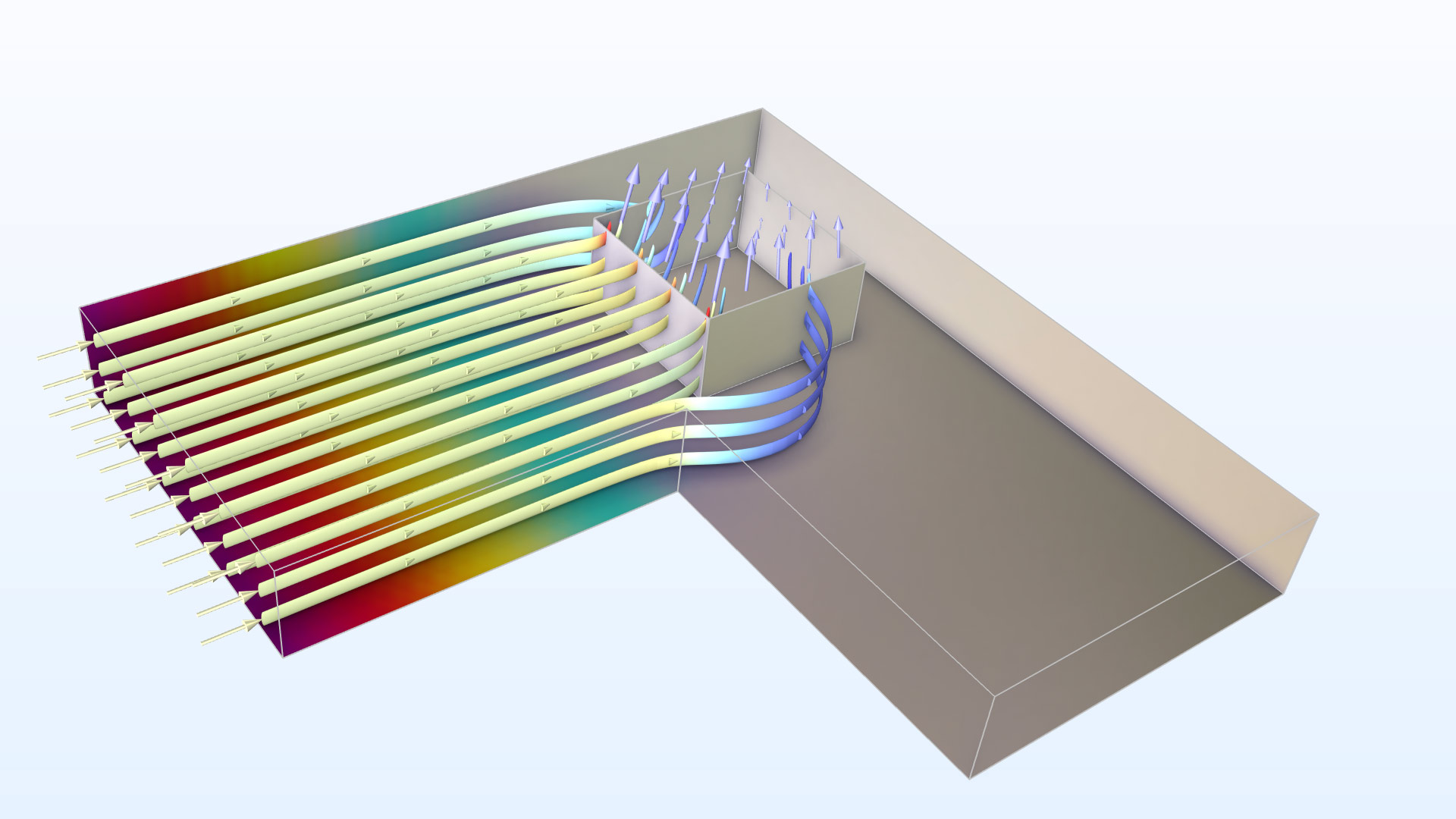
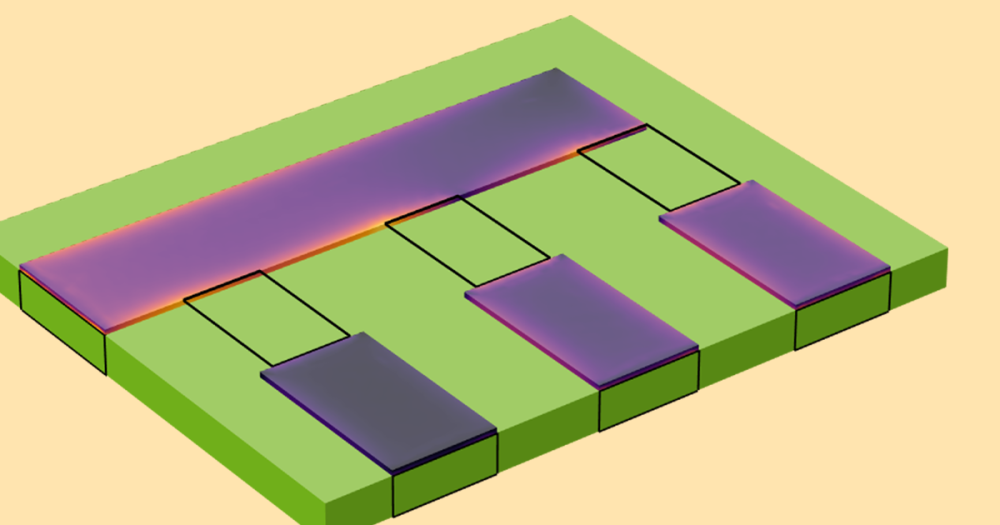
用于接触电阻测量的跨桥开尔文电阻器的电势(颜色)和电流密度(箭头和流线)模拟。
所研究结构的核心是一个 5000 Å 厚的 n+ 掺杂的多晶硅层,其图案是一个“L”形,如上图所示。给“L”的左臂通入电流,并通过一个方形的接触窗口流出到上面的金属层,如箭头所示(金属层在图中没有明确显示)。桥式电压表用于测量“L”的右臂和金属层之间的电压降。
这个结构产生一个可以直接测量的量,即开尔文接触电阻 R_c(SI 单位:Ω),它可以通过将电压降除以流过接触窗口的总电流获得。但是这个电阻值并不是表征接触的一个很好的量,因为它会根据测试结构的尺寸而变化。这是由于通过接触窗口的电流密度分布不均匀(电流拥挤效应,如上图中箭头的不同长度所示)。
金属-半导体接触的性质可以由另一个量更好地表征,即 比接触电阻率 \rho_c(SI 单位:Ω m2),它被定义为:局部电压降除以无限小的接触面积单元内的法向电流密度。这个量不能直接测量,必须使用数值模拟从测量的 R_c 值中提取。
提取比接触电阻率
由于测试结构尺寸的变化,参考文献1报道了两组测量值 R_c。在第一组实验中,接触窗口的尺寸(l)在 5.0 到 65 μm 之间变化,而“L”的两个臂的宽度(扩散抽头宽度,w) 始终比 l 大 5 μm。在另一组实验中,扩散抽头宽度 w 在 7.5 到 60 μm 之间,而接触窗口尺寸 l 保持在 5 μm 不变。这些实验产生的数据 R_c–l 和 R_c–w 可用于提取比接触电阻率 \rho_c,通过使用不同的 \rho_c 值进行数值模拟,并找出实验数据和模拟数据 R_c–l 曲线和 R_c–w 曲线之间的最佳拟合。
参考文献1的作者选择了二维近似模型进行数值模拟。参考文献2中对这个二维模型进行了详细描述,简单来说,类似于 COMSOL 半导体模块提供的模型,从三维模型开始,忽略了肖特基带弯曲和少数载流子效应(假设理想欧姆接触),只考虑多数载流子。金属的电导率远高于半导体,因此假定金属内的电势在整个接触窗口上是均匀的。
近似二维模型
为了将三维模型简化为近似二维模型,假设半导体的电导率在面内方向上是均匀的,并且电导的厚度方向依赖性被归结为一个参数,薄层电阻 R_s(SI 单位:Ω)。在假设金属接地和传输长度 l_t (\equiv\sqrt{\rho_c/R_s},SI 单位: m) 大于 n+ 掺杂层的厚度的情况下, 用一个简单的二维方程可以推导出一个新的变量,电导率加权平均电位 V_{2D}(SI 单位:V)。该方程是
(1)
在接触窗口下,该方程为
(2)
式中,拉普拉斯算子的下标 t 表示面内(切线)方向。对于这个二维模型,面内电流密度可以被评估为
(3)
并且通过接触窗口的正常电流密度由下式给出
(4)
在这个教程示例中,构建了三维和二维模型并比较了二者的结果。
三维模型设置
使用半导体 接口可以直接设置三维模型,在接触窗口处的 金属接触 边界条件启用接触电阻 选项。
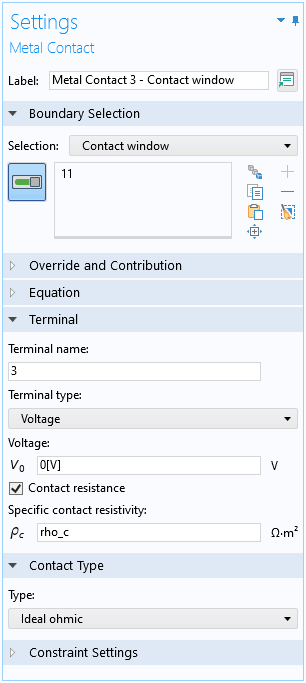
接触窗口的 接触电阻 选项被激活。
对于左侧终端的边界条件的设置,不使用输入电流,而是施加一个小电压 V0,以便于收敛。使用内置变量求解后,可以轻松评估输入电流。对于右边的终端,假设电桥电压表具有无穷大的阻抗,因此对金属触点施加零电流边界条件,测得的电压降对应于求解后的终端电压。
按照默认的有限体积离散化的要求使用扫掠网格。网格被参数化,以便在扫描测试结构的尺寸时保持接触窗口周边的分辨率。
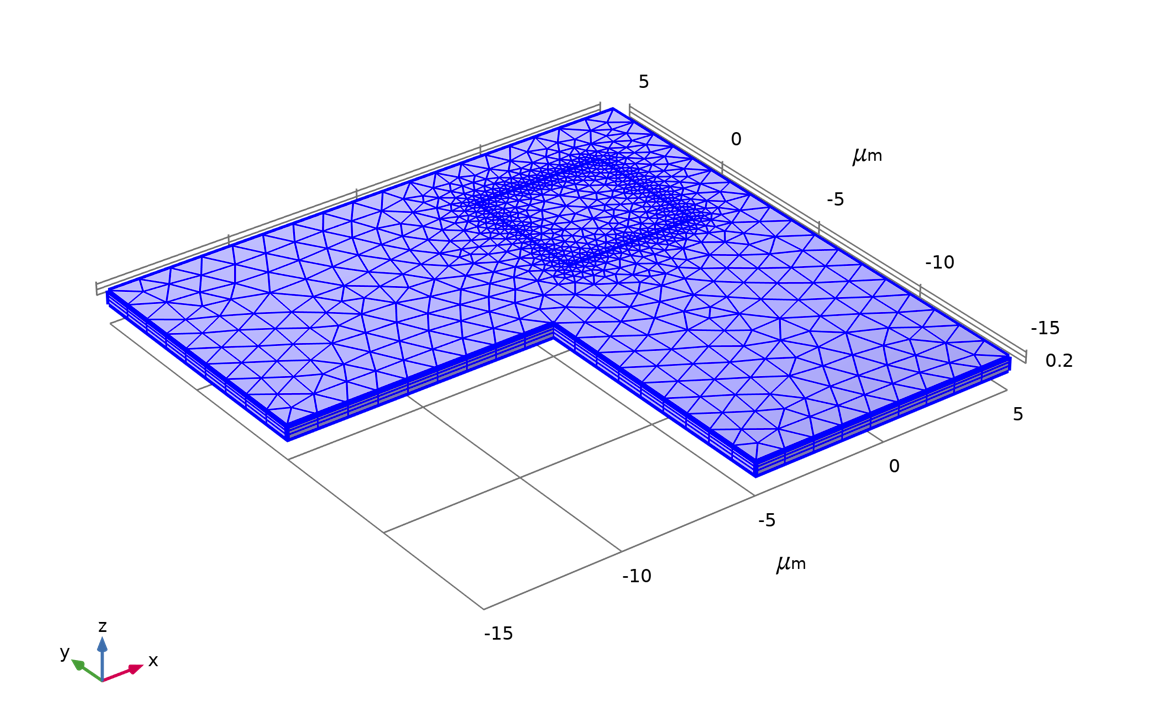
模型中使用的网格示例。
二维模型设置
使用一般形式边界偏微分方程 数学接口,在用于三维模型的同一几何图形的顶面上轻松创建自定义方程1~方程4的二维模型。由于这个数学接口“存在”在表面上,因此“域”是二维表面,“边界”是一维边。将因变量命名为 V2D 来表示方程中的变量 V_{2D}。
方程1和方程2的左侧是相同的,可以使用默认的一般形式偏微分方程域条件来实现,从保守通量的默认表达式中删除减号,并将 源项 和阻尼系数 设置为零以与方程的左侧匹配,如下面的屏幕截图所示。(保守通量向量 {V2DTx,V2DTy,V2DTz} 表示电导加权平均电位的切向梯度 \nabla_t V_{2D})
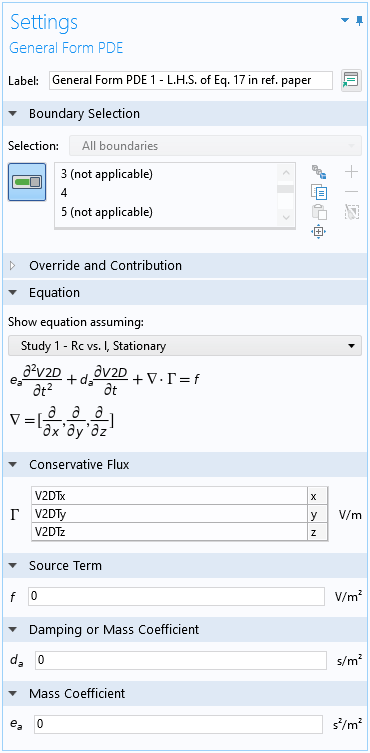
默认的一般形式偏微分方程域条件的设置窗口。
对于方程1 的右侧,在接触窗口中添加源 域条件,并在 源项 输入中 输入 V2D/lt^2 表达式,对应于公式右边的 \frac{V_{2D}}{l_t^2}。
使用 Dirichlet 边界条件对左侧纵端施加与三维模型中相同的小电压 V0。为了根据等式3 获得准确的电流密度,启用使用弱约束 复选框。这将指示软件在边界上创建和求解拉格朗日乘数V2D_lm。我们可以使用它通过表达式 等式 V2D_lm[V/m]/Rs 来计算法向输入电流密度,对应于等式3中给出的公式。然后可以通过使用积分算子对边界上的电流密度进行积分来计算端子处的总输入电流。
对于右终端,也施加一个具有弱约束的狄利克雷边界条件,现在具有一个未知的施加电压 V2D_ode。添加一个全局方程 节点来求解未知数 V2D_ode,使得终端电流为零(假设电桥电压表的阻抗在三维模型中是无限的)。终端电流是用拉格朗日乘数以与左终端类似的方式计算的。
最后,根据等式4 中的公式,流出接触窗口的法向电流密度的表达式为 V2D/rho_c。
研究和结果
在参考文献1中的两组实验之后,使用参数扫描创建了两个研究来改变接触窗口的大小 l 和扩散抽头宽度 w。(请注意,不能使用辅助扫描来改变几何形状或网格)。
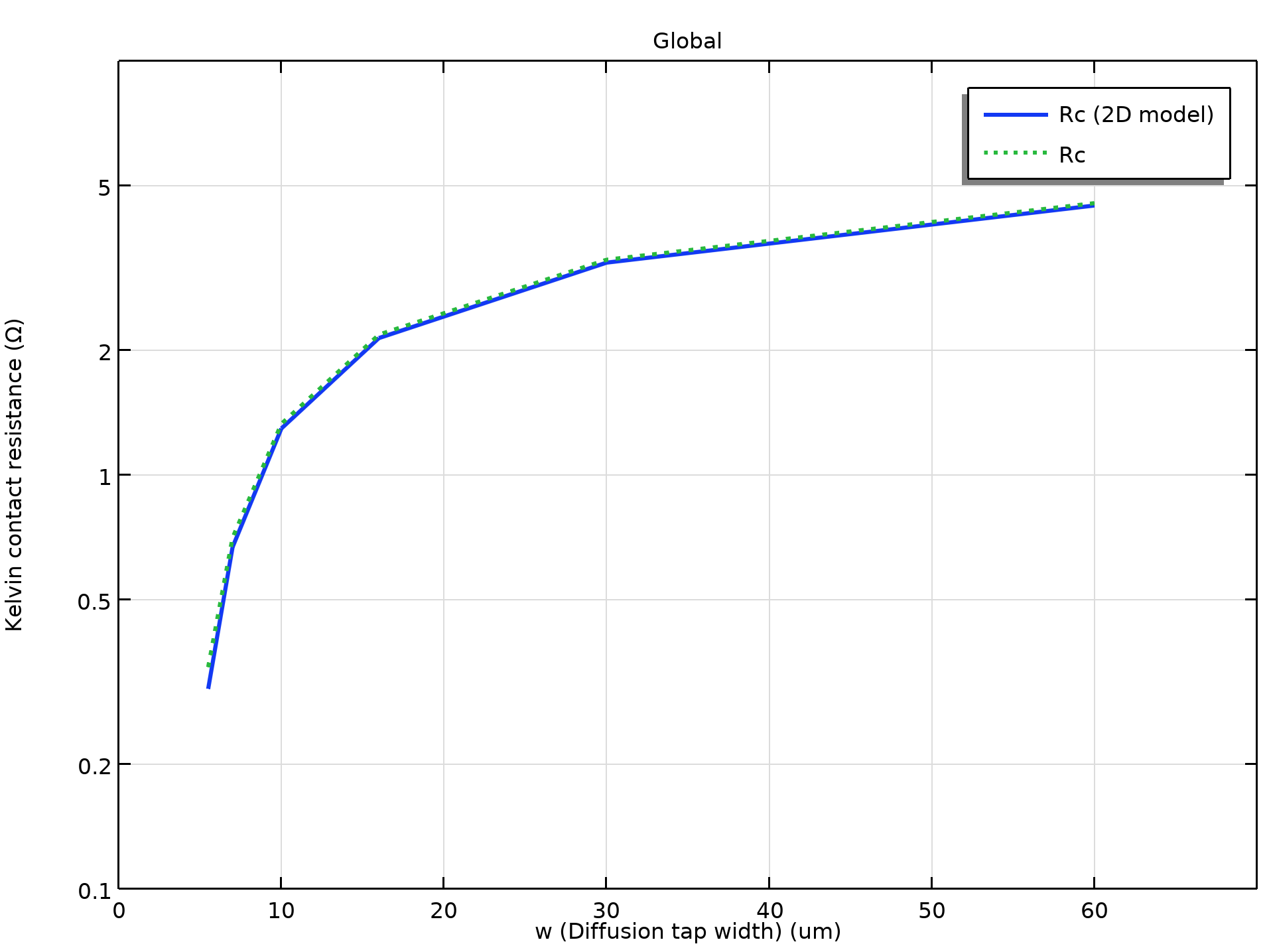
使用特定接触电阻率的最佳拟合值 \rho_c (4.5e-8 Ω cm2) 作为模型的输入,模拟的开尔文接触电阻 R_c 与接触窗口面积 l^2 和扩散抽头宽度 w 绘制在下面的两个图中。
模拟的开尔文接触电阻 R_c 与接触面积 l^2 和扩散抽头宽度 w。实曲线:二维模型;虚线:三维模型。
我们看到,二维和三维模型的模拟结果非常相似,并且与论文中的数值非常吻合。
结语
在这篇博文中,我们演示了在金属接触 边界条件中使用 接触电阻 特征。我们还展示了使用软件内置接口进行基于方程的建模是多么简单!欢迎您在下方评论中留言,告诉我们您是如何利用 COMSOL Multiphysics 的灵活性和多功能性进行仿真工作的!
自己尝试
单击下面的按钮,进入 COMSOL “案例库”,下载 MPH 文件,尝试自己模拟跨桥开尔文电阻器,并提取特定的接触电阻率:
参考文献
- W. M. Loh, S. E. Swirhun, E. Crabbe, K. Saraswat and R. M. Swanson, “An accurate method to extract specific contact resistivity using cross-bridge Kelvin resistors”, IEEE Electron Device Letters, vol. 6, no. 9, pp. 441–443, 1985, doi: 10.1109/ EDL.1985.26185.
- W. M. Loh, S. E. Swirhun, T. A. Schreyer, R. M. Swanson and K. C. Saraswat, “Modeling and measurement of contact resistances”, IEEE Transactions on Electron Devices, vol. 34, no. 3, pp. 512–524, 1987, doi: 10.1109/T-ED.1987.22957.






评论 (12)
h恒源 许
2022-05-07你好,刘老师,请问您的后处理“流线和箭头”是怎样做到这种的呀,请问能否给出教程呀!非常感谢
Qihang Lin
2022-05-10 COMSOL 员工教程模型已在博客最下方放出,您可以检查其中的后处理设定:https://cn.comsol.com/model/a-cross-bridge-kelvin-resistor-model-for-the-extraction-of-specific-contact-resi-99621
120 W
2022-09-20刘老师,您好,请问金属接触这个选项和接触阻抗里的表面电阻选项有什么区别?
Qihang Lin
2022-10-10 COMSOL 员工金属接触这个功能是用在外表面的,未勾选接触电阻选项的话默认是理想接触,一般都是用于激励。接触阻抗的话适用于内表面薄层简化,并不通入任何激励,同时当亲半导体接口中还没有内置这种边界条件。
120 W
2022-10-17请问应该如何理解您这里“激励”的意思。另外想询问是否能使用“电流”模块中的“接触阻抗”中的“表面阻抗”一项 来反应上层金属和下层半导体材料之间的欧姆接触,我看单位也是Ω.m^2。
Qihang Lin
2022-10-26 COMSOL 员工激励:在设置金属接触的时候可以设置终端电极的电压大小,一般用于模拟金属电极提供的激励条件,由于界面与界面之间接触可能会受表面粗糙度等因素影响,因此可以接触电阻来模拟此类情况。您提到使用电流模块中的表面阻抗相当于将其中带有粗糙度的接触面使用表面阻抗等效,只要您能够获取到其数值就没有问题。
子章 康
2023-04-14刘老师您好,在模拟电热力物理场耦合时,因为接触面之间有力的作用所以几何部分使用的是“形成装配体”,但由于接触面形成了接触对,使得无法在“电流”模块中将接触面设置为“接触电阻”(无法选中,“形成联合体”时才可以选中),请问怎样在考虑压力作用的情况下设置接触电阻呢?
Qihang Lin
2023-04-18 COMSOL 员工使用装配体时请在电流接口中使用 “对,电接触” 或 “对,接触阻抗” 功能,这个功能被折叠在了 “对” 分类下。您的情况可以考虑 “对,电接触” 条件,其中内置两类接触压力对接触电阻的影响公式。您可以参考 “接触开关” 案例,此案例模拟了开关的两个接触部分的热性能和电性能,其中电流和热量仅通过接触面从一部分传递到另一部分:http://cn.comsol.com/model/contact-switch-4119
春晨 荣
2023-07-07你好,刘老师,我想做一个金属与金属的接触来得到其接触电阻的变化曲线,我想输出比接触电阻率可以吗
Qihang Lin
2023-07-31 COMSOL 员工金属接触仿真可以参考案例:http://cn.comsol.com/model/contact-switch-4119
在后处理中可以提取边界上的接触电阻率。
Dong Xu
2024-03-08老师您好,板之间设置接触对,两板贴近和远离对结果有影响吗?
我在建几何模型的时候两块板之间无法设置接触对,出现这种情况是什么原因?请问可以解答一下吗,谢谢!
Hao Li
2024-03-11 COMSOL 员工您好!
感谢您的评论。
接触对是当两个面接触时接触对才会起作用。
无法设置可能是因为几何只有形成装配体时才可以设置接触对,若设为装配体仍无法建议将问题发送到Support系统中,以便确定具体问题。
cn.comsol.com/support
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!