
我们已在求解器系列的部分博客中讨论了求解非线性静态有限元问题、用于改善非线性问题收敛的载荷递增,以及用于改善非线性问题收敛的非线性递增。我们还介绍了线性静态问题网格剖分的注意事项,以及在网格剖分过程中如何找到奇异性并对此进行处理。在本篇博客中,我们将基于上述内容解释如何准备网格,以便能高效地求解非线性稳静态有限元问题。
对线性和非线性静态问题的回顾
您是否还记得“线性 静态问题的网格剖分注意事项 ”博客中提到的三个关键点:
- 经过一次 Newton-Raphson 迭代后,不论网格尺寸大小,线性静态有限元问题都会收敛。
- 您应选择从尽量粗化的网格开始,然后手动细化网格或是使用自适应网格细化,使用更细化的网格求解。
- 应当使用网格细化评估结果的精确度,同时使收敛远离模型中的奇异性。
我们还了解到,当求解非线性问题时,即使包含单一自由度且有解的有限元问题也可能不收敛。我们已经学习过处理这种问题的几种方法,但尚未介绍网格和非线性求解器之间的相互作用。
非线性问题的网格剖分
对非线性问题进行网格剖分时应熟记以下内容:
就算问题本身很完善、我们也选择了一个好的求解方法,但如果没有在强非线性区域内进行足够的网格剖分,问题也可能不收敛。
为了更好地理解上述内容,我们将研究一个一维传热有限元问题。考虑 1 m 厚的墙,一端温度恒定为T=0 ,另一端温度恒定为 T=100 ,如下图所示:
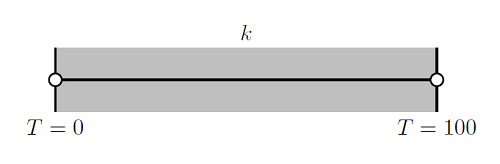
我们将检验不同热传导率下问题的解,如下图所示:
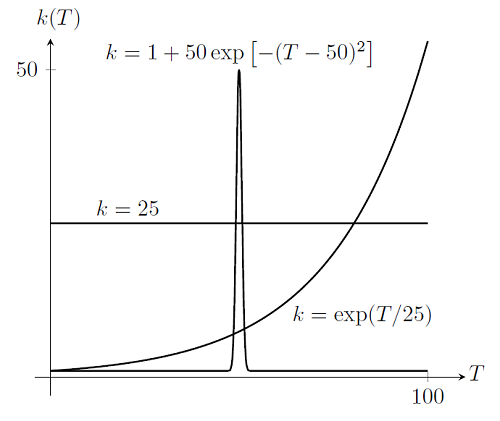
如果绘制线性情形 k=25 的解,将得到:

经检验后,我们发现解是一条直线。对于这种情况,整个域内使用单一线性单元即可求解。
现在,如果我们要绘制 k=\exp(T/25) 时的解,并用虚线表示各个单元,将得到:
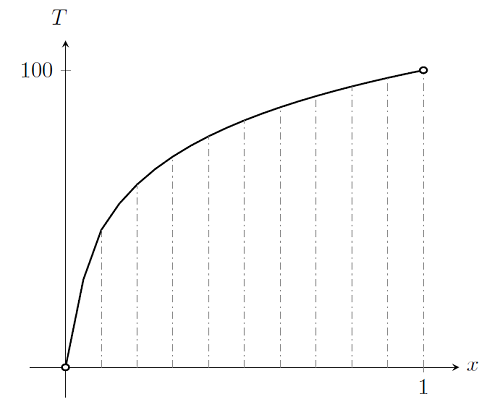
我们发现这种非线性问题的解要求域内要有多个单元。实际上不管我们使用多少单元,多项式基函数都不会完美匹配真实解。我们可以在域内任何一处成功细化网格并无限接近真实解,就如同处理线性问题一样。
最后,如果我们绘制 k=1+50\exp\left[-(T-50)^2\right] 时的解,将得到:
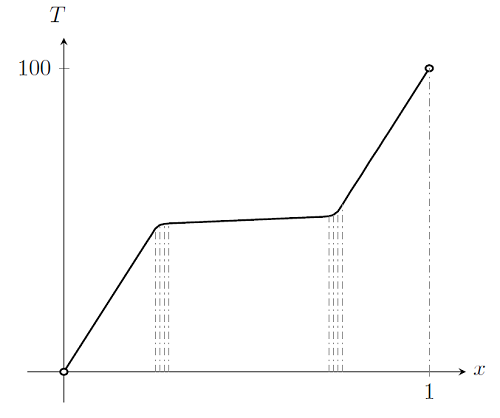
这个解更为复杂。很明显解内存在单靠一个单元无法充分描述的区域。当然也存在解会随位置的函数迅速变化的区域。这些区域都在 T=50 附近,周围的材料属性函数中存在强非线性。尽管材料属性函数的温度部分只存在一个强非线性区域,但解会在域内的两处区域变化迅速。只有这些区域需要更细化的网格。实际上,当这些区域中的网格太过粗化时,求解器可能完全不收敛。
此类问题就可以使用自适应网格细化求解,因为建模域内的梯度位置总体上是未知的。非线性递增同样十分有用,因为不论网格尺寸,从一个线性问题出发总能得到一个可以求解的问题。通过逐渐递增非线性以及循环使用自适应网格细化,将能够改善非线性问题的模型收敛。
总结
历来,非线性静态有限元问题的网格剖分都和非线性模型的收敛相关。除了收敛速度,收敛概率也都依赖于求解器算法和所使用的网格。到目前为止我们已经介绍了许多求解技巧,包括手动及自适应网格细化、对初始条件的选择、载荷递增、非线性递增,以及上述方法之间的任意组合,您将会在进行更为复杂的建模时用到这些技巧。最后,还请记住我们需要网格细化研究来评估解的精确度。
如果希望获取一个综合了上述所有求解方法的模型示例,请点击访问金属的冷却和凝固模型。熟练掌握以上方法后,您将能更高效、快速地进行非线性问题的建模。





评论 (1)
建华 金
2017-06-06可以