
今年 7 月,我有幸参加了第 22 届国际声与振动大会。在会上,除了与我的意大利同事 Gabriele 一起管理 COMSOL 供应商的展位外,我还做了一个演讲。我的演讲内容基于我与 Henrik Bruus 和 Jonas Karlsen 写的一篇论文,主要是关于如何确定包括热黏性效应的声辐射力。今天这篇博客,我们来进一步详细地探讨声学辐射效应和我演讲中重点介绍的研究结果。
什么是声辐射力?
声辐射力是由于声场对微小粒子的动量传递而产生的作用在粒子上的净力。在与之相关的声流现象中,净流体流动是由声场驱动的,其中动量传递(到流体)发生在声学边界层。
这两种现象都很重要,例如在微流控装置中,可用于移动、控制和分类粒子或小型有机体(即细胞、蛋白质或大型病毒)。这种粒子控制被称为声泳,也就是由声音产生的运动。辐射力直接作用于粒子,而声流则在粒子上诱发的曳力。声泳效应的大小和/或方向取决于粒子的大小和力学特性,以及流体特性。充分理解这类现象对于生产和优化用于有效分拣和控制粒子的装置至关重要。在之前的一篇博客中演示了如何在微流控装置中模拟声辐射力和声流。
在篇文章是对如何使用二阶扰动理论 对声辐射力进行详细建模的扩展和概述。声辐射力系列博客介绍了如何理解辐射力以及计算这些力的不同方法,欢迎阅读。
分析声辐射力的不同方法
现在,让我们来讨论几个技术性问题,先看几个方程。像大多数物理问题一样,在不同的物理假设和不同的规则下,有多种描述和推导辐射力效应的方法。接下来,我将对这些不同的方法简要地进行总结和描述。
直接流-固耦合作用法
在直接流-固耦合作用(FSI)方法中,(非线性)控制方程组被看作一个动态问题来求解。然后通过观察时均粒子运动来获取辐射力。为了考虑热损失和黏性损失,需要同时求解纳维-斯托克斯方程与能量方程,这本质上是一个非等温流动问题。这些方程应该以高数值精度求解,用于计算与辐射力相关的所有小尺度效应。
二阶扰动法
为了简化对非线性控制方程组的分析,可以将问题拆分为一个线性声学问题和一个二阶线性时均问题。这是通过二阶扰动理论完成的。例如,压力 p 可以写成 p = p_0+p_1+p_2。下标 0 代表背景属性(0 阶压力可以粗糙地认为是一个由平衡条件决定的恒定大气压),下标 1 代表经典声场,下标 2 代表描述非线性效应所需的二阶扰动场。不同阶次的方程是按顺序求解的。
由这个理论可以确定,一般情况下,物体 \Omega 的辐射力由以下公式给出
(1)
其中 \langle \cdot \rangle 代表时均,\sigma_2 是对应力的二阶贡献,\mathbf{u}_1 是速度场的声学变化,积分是在粒子周围的任意一个封闭表面。
因此,为了计算辐射力,必须同时求解声学问题(一阶扰动)和二阶扰动方程。我在 ICSV22 会议上发表的研究中使用了这种方法,接下来我将对细节进行更详细地讨论。对方程进行求解,包括计算流体和固体的热损失和黏性损失。
无损耗假设
对于远大于黏性和热边界层的尺寸为 a 的粒子(穿透深度为 \delta_\textrm{tv}),也就是 \delta_\textrm{tv}/a \ll 1,流体可以被看作无损失。在这种情况下,公式(1)中的二阶应力在远场可以简化为
(2)
通过确定任意物体的散射场 p_1 和 \mathbf{u}_1,可以计算出公式(1)中的辐射力。没有必要明确地知道二阶场的情况。下一篇博客 “如何计算声辐射力“中的参考文献2 提供了 2 个这方面的例子。
瑞利假设
在瑞利假设中,假定粒子是声学上的小粒子。也就是说,k\cdot a \ll 1 ,其中 a 是粒子大小,k 是波数。使用散射理论来推导粒子上的散射场。在这个假设中,公式(1)中给出的辐射力降低为
(3)
_\textrm{rad}= -2\pi a^3 \left[ \frac
{1}{3} \kappa_s \textrm{Re} [f_0^* p_\textrm{in}^* \nabla p_\textrm{in}]-\frac{1} {2}
\rho_0 \textrm{Re}[f_1^* \mathbf{u}_\textrm{in}^* \cdot \nabla \mathbf{u}_\textrm
{in}] \right]
其中 f_0 和 f_1 是单极和偶极散射系数,下标 \textrm{in} 代表在小颗粒位置上评估的入射声场(例如,分选装置中的驻波声场)。\kappa_s 是流体可压缩性,\rho_0 是流体密度。这种方法的所有操作包括计算 2 个散射系数。以下是存在解析解的一些情况:
- 对于无黏性和绝热的情况,参考文献3 中由 Gor’kov 给出的结果。
- 参考文献4 中由 Settnes 和 Bruus 给出的包括黏性的结果。
- 参考文献5 中,由 Karlsen 和 Bruus 给出的完整的热黏性理论不仅求解了一个小液滴的散射,还求解了粒子内部的热黏性效应。
- 有关这个领域的许多成果,您可以查看关于悬浮声学的相关研究 (见文献6)。
COMSOL Multiphysics 中基于方程的建模方法
第一个模型系统,我们决定求解放置在超声驻波中的球状小粒子上的声辐射力。如上所述,我们选择使用(公式1)中给出的详细的扰动方法来计算辐射力。该模型包括流体和固体的热损失和黏性损失。
第一步是求解声场(一阶声场);换句话说,就是求解与固体热弹性接口 耦合的流体热黏性声学、频域 物理场接口中的方程。所需的耦合在 COMSOL Multiphysics 中没有预定义,但可以在用户界面(UI)中轻松设置。然后,COMSOL Multiphysics 就可以解决完全耦合的问题。
建立好一阶场后,就可以求解二阶方程的时均方程。因此,从这里开始,我们将省略二阶量的 \langle \cdot \rangle 符号,只要它出现在方程中,就将被理解为时均值,即 \langle a_2 \rangle \equiv a_2。
这些方程的结构与 CFD 模块中的层流方程是相同的,只是增加了源项。由于数值上的原因,我们不使用预定义的方程,而是使用自定义的保守形式的方程。这一步对于减少从一阶场传播到二阶解的数值噪声很重要。在非保守公式中,一阶场的梯度需要显示计算,因此会引入数值噪声。质量、动量和能量守恒的方程如下所示:
(4)
\nabla\cdot[\rho_0 \mathbf{u}_2+\langle \rho_1 \mathbf{u}_1 \rangle] = 0 \\
\nabla\cdot [\mathbf{\sigma}_2 – \rho_0\langle\mathbf{u}_1\mathbf{u}_1^\textrm{T}\rangle \mathbf] = \mathbf{0} \\
\nabla\cdot [k \nabla T_2+\langle \mathbf{u}_1\cdot\mathbf{\sigma}_1\rangle + \alpha_0 T_0 \langle p_1 \mathbf{u}_1 \rangle – \rho_0 C_\textrm{p}\langle T_1 \mathbf{u}_1 \rangle] = 0
\end{aligned}
这里假定二阶场是时均值。请注意,一阶场在二阶方程中起着源项的作用。
设置方程和边界条件只能使用 COMSOL Multiphysics 中的一般弱形式。能够灵活增加和定义新方程对于求解这个问题至关重要。
结果
我们已经介绍了理论和方程,现在我们来看使用 COMSOL 模拟的一些漂亮的彩色结果图。
我们来看一个半径在 a=1 \: \mu \textrm{m} 到 a=40 \: \mu \textrm{m} 的球状聚苯乙烯小粒子。该粒子被空气包围,位于一个 2MHz 的超声驻波场中,且 \delta_\textrm{v} = 1.6 \: \mu\textrm{m} 和 \delta_\textrm{t} = 1.9 \: \mu\textrm{m}。因此,对于较小的粒子来说,边界层效应预计是显著的,无损理论是不准确的。此外,对于大粒子来说,除瑞利极限之外的 k\cdot a \ll 1 的粒子,所选择的颗粒子尺寸范围为 0.04 < k\cdot a < 1.5。这意味着我们的分析超出了理论的范围。
振荡的声压场。
上面的动画描述了总的谐振声压场 p_1。黑色圆圈代表使用公式(1)计算时的不同积分面,但它们也被用来控制计算网格。粒子上的散射场如下图所示。由于非线性效应,这种谐波压力振荡会产生一个净时均辐射力。
粒子上的散射场。
以下一系列动画说明了一系列仿真分析的结果。在最上面一排,左边的图描述了围绕着粒子的温度波动 T_1。温度变化的范围表明了热边界层或对流体的穿透深度。右图显示了聚苯乙烯小颗粒的变形,以及固体中的一阶温度变化。这里,再次模拟了固体内部的热穿透深度。在最下面一行,左边的图表示散射声场的轴向速度分量,右边的图表示这个声场的径向速度分量。
一系列仿真分析的结果。左上:温度的变化。右上:粒子的变形。左下:散射声场的轴向速度分量。右下:径向速度分量。
我们可以将一阶场插入二阶方程中,然后求解粒子周围的局部稳态流,见公式(4)。压力和速度的大小分别显示在下面两个图中。请注意压力(单位:Pa)和速度(单位:m/s)的刻度非常小(用颜色条表示)。以相对于入射驱动波的压力为例,它的振幅为 3\cdot 10^{-3} \: \textrm{Pa}。
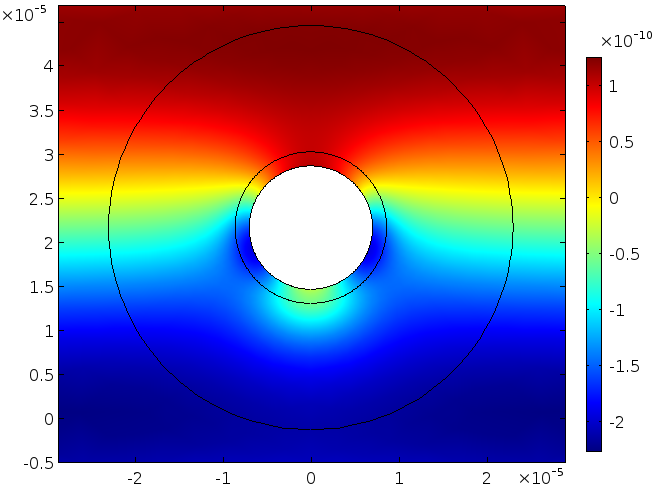
压力场。
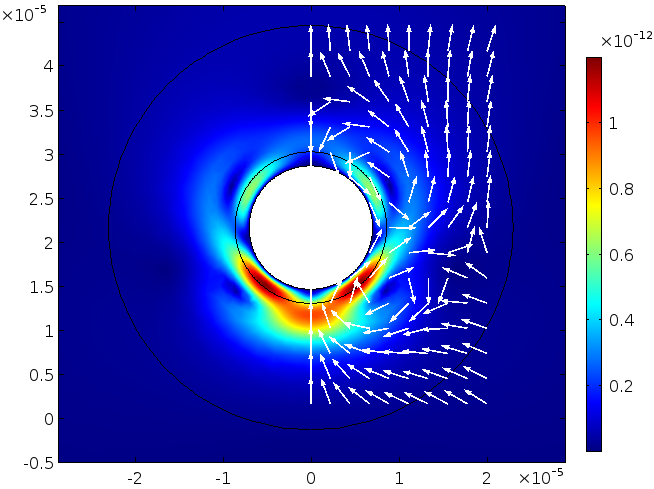
速度场。
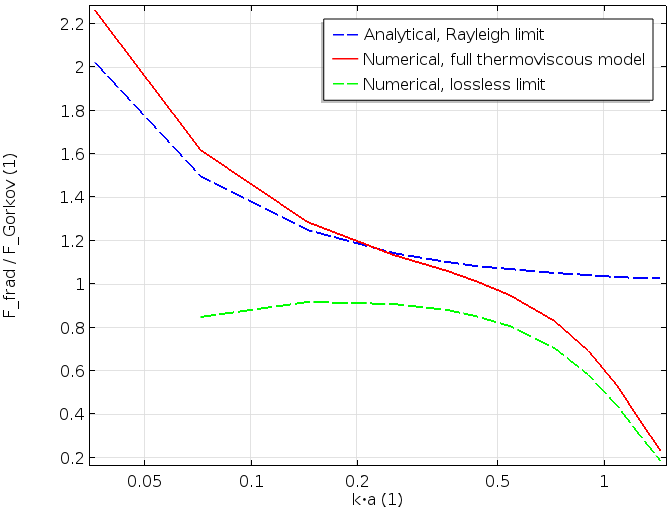
最后,知道了一阶和二阶场后,我们就可以推导出公式(1)中给出的力。在第一张图中,该力被描述为 \delta_\textrm{v}/a(黏性穿透深度与粒子大小的关系)的函数。在第二张图中,它被描述为 k\cdot a 的函数。声辐射力使用在无损耗假设情况和瑞利假设情况下计算的力进行无量纲化(用 Gor’kov 表示)。
这些图包括三条曲线。蓝色虚线曲线是 Karlsen 和 Bruus 在瑞利极限下给出的分析表达式。绿色虚线表示用无损模型(不考虑边界层)计算的力,由公式(2)给出。最后,红色曲线表示完整数值模型,包括热黏性损失,它对大颗粒和小颗粒都有效。
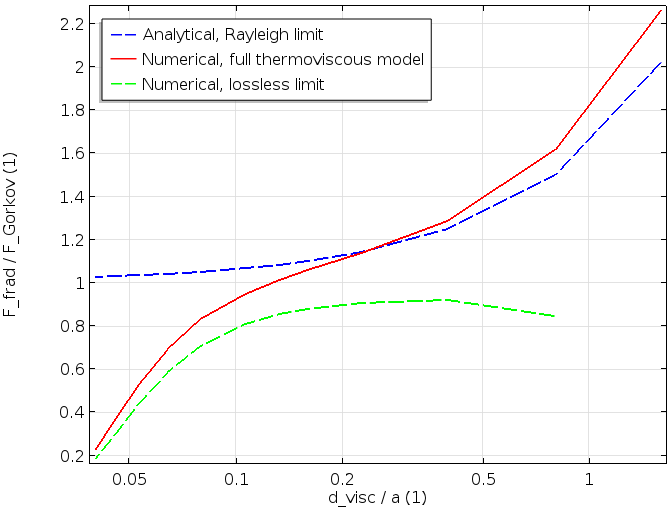
第一张图(如上图所示)说明了含黏性损失和热损失的完整模型是如何将无损失的(\delta_\textrm{v}/a 很小)与蓝色曲线相关联的,后者包括损失,但只对小粒子有效(对于恒定材料参数,\delta_\textrm{v}/a 较大)。下面描绘的第二张图显示了同样的特征。可以看到,我们建立的详细热黏性模型与大颗粒子假设(绿色虚线无损耗)和小粒子极限假设(蓝色虚线,瑞利极限下的小粒子 k\cdot a)之间的联系。
结束语
本文是我与 Henrik Bruus 和他在 Technical University of Denmark 的研究团队一起进行的一小部分研究。在进行实验和数值建模的同时,研究团队的工作对声致伸缩现象理论的深入理解起到了促进作用。
本文侧重于对作用于球状小粒子(计划在未来研究中使用的椭圆粒子)的辐射力进行新的完整的热黏性数值分析。该模型的模拟结果与现有的适用限制(瑞利假设和/或无损耗假设)的计算结果很一致。由于这种方法通用性很强,因此可以很容易地扩展到任意形状的颗粒。该模型还可以进一步扩展,包括更详细的材料依赖性,如黏度随温度的波动。
扩展阅读
- “Theory and Simulation of the Acoustic Radiation Force on a Single Microparticle in an Ultrasonic Standing Wave Including Thermoviscous Effects”, M. J. H. Jensen, J. T. Karlsen, and H. Bruus.
- “Efficient finite element modeling of radiation forces on elastic particles of arbitrary size and geometry”, P. Glynne-Jones, P. P. Mishra, R. J. Boltryk, and M. Hill.
- “On the forces acting on a small particle in an acoustical field in an ideal fluid”, L. P. Gor’kov.
- “Forces acting on a small particle in an acoustical field in a viscous fluid”, M. Settnes and H. Bruus.
- “Forces acting on a small particle in an acoustical field in a thermoviscous fluid”, (accepted) J. T. Karlsen and H. Bruus.
- Suspension Acoustics: An Introduction to the Physics of Suspensions, S. Temkin.






评论 (2)
琪琪 齐
2023-05-23请问这篇博客有相对应的仿真文件嘛?
Qihang Lin
2023-06-01 COMSOL 员工没有,请查阅最底下列出的文献自行复现。