
我想您一定记得上次因流感而卧床的情景。流感俗称感冒,这对我们而言可能只是一次很不愉快的体验,但其实它每年还会造成大量的人员伤亡。现在,公共卫生官员正借助数学仿真技巧研究流感和其他传热性疾病,希望能预测它们的传播,并据此做出明智的公共卫生决策。
流行病:一个危险的健康威胁
纵观整个人类发展史,我们始终都在应对各种传染病和流行病问题。在中世纪的欧洲,大约 1/3 的人口死于鼠疫的爆发,也就是黑死病。1918 年,第一次世界大战刚刚结束后就爆发了流感的大流行,造成了将近一亿人口的死亡。最近爆发的 SARS、流感和埃博拉等流行病也给我们的公共安全带来了严重的威胁。不论在发达国家还是发展中国家,流行病都会影响国家的经济与社会稳定。
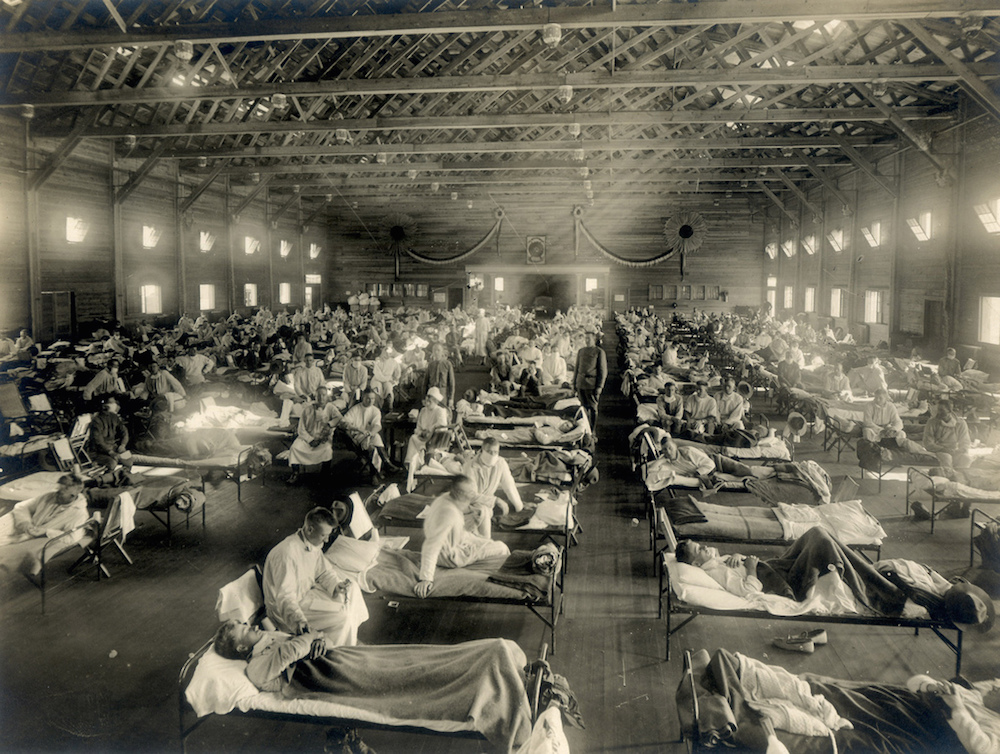
流感大流行时美国堪萨斯州 Funston 军营的应急医院。
面临疾病威胁时,医疗专业人士和公共卫生必须做出相关决策来阻止并预防流行病的传播,此时需要考虑以下问题:
- 正确的预防或控制策略是什么?
- 能通过大规模疫苗接种改善吗?什么时候接种?
- 是否应该对特定的地理区域执行集体隔离?
- 为了阻止疾病的传播,是否应该临时暂停飞机、火车或汽车等交通方式的使用?
我们必须快速高效地做出此类决策。否则,疫情可能快速蔓延,严重威胁全球健康。
历史上就曾出现过因采取了错误的控制措施而使情况进一步恶化的例子。1665 年,英国 Eyam 村爆发了黑死病。故事是这样开始的,一位当地的裁缝从伦敦订了一块布料。当时的伦敦正爆发我们称作伦敦大瘟疫的疫情,这块布料也因携带瘟疫的鼠疫蚤被感染。疫情持续扩散并一直持续到 1666 年底,使村民人数从 350 减少到 83 人。
村民曾向当地的教会领袖求助,后者建议他们在自己的房子中进行隔离。这阻止了疾病向邻村的进一步传播,但由于村民们曾与受感染的老鼠有过密切接触,且一直保持接触,于是引发了第二波疫情。疫情不仅在老鼠与人之间传播,还通过人际接触进行传播。因此,Eyam 村的死亡率远高于伦敦。Eyam 村的鼠疫爆发留下了详细的文字记录,人们甚至专门建立了一家博物馆来向后世讲述这个故事。
我们可以从这类历史案例中获取很多信息,不过它们只能为我们提供粗略的指导。我们很难执行流行病学实验:除了严肃的道德方面的考虑,还存在数据不完整或完全缺失等问题。解决方案之一是数学建模,这也是目前许多国家及国际公共卫生组织的做法。
借助仿真应对流行病的爆发
流行病数学模型有一段相当传奇的历史,它始于 18 世纪的天花大爆发,不过现在我们已经彻底根除了这种传染病。天花曾是一种很严重的传染疾病,致死率一度超过 30%,人们发现所有活下来的人群都对此产生了免疫能力,并因此发明了名为天花接种的方法,即人为使接种对象,感染少量天花病毒。如果一切顺利而且病人运气很好的话,复原率会非常高,并将从此对这个疾病免疫。
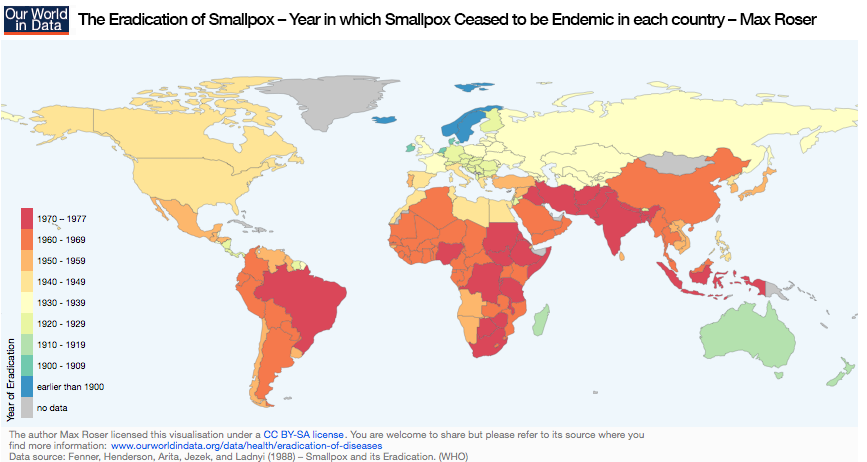
天花在世界各地的绝迹年份图。图片为 Max Roser 自行制作。已获 CC BY-SA 4.0 授权,并通过 Our World in Data 分享。 您可以点击该页面,获取更多相关信息。
1760 年,法国数学家 Daniel Bernoulli 在巴黎皇家科学院展示了他对天花致死率的研究,演示了普遍接种疫苗对该危险疾病传播的影响。
Bernoulli 开发了世界最早的流行病学数学房室模型。后来学者纷纷采取了该做法,1900 到 1935 年间数理流行病学逐渐发展成为一门专门的学科。以下科学家也为此做出了重要的贡献,包括因发现蚊子是疟疾的传播媒介而获得诺贝尔奖的 Ronald Ross 爵士,以及 Anderson Gray McKendrick 和 William Ogilvy Kermack,他们基于一些相对较简单的假设开发了一个房室模式来预测流行病的行为。
今天,对传染病进行数学建模已经成为一个非常活跃的领域,有望拯救无数的生命。医学研究人员和公共卫生医师们借助这些模型来理解流行病的流行以及寻找一些基本问题的答案,比如:
- 流行病有多严重?
- 多少人会感染?
- 最有效的控制或治疗策略:隔离或接种疫苗?
模型帮助弥补了这些数据缺口,并预测了流行病的最终结果。
我们将研究 McKendrick 模型中的一个变体,SIR 模型。这是一个房室模型,将整个人口分配在不同的房间内:S 代表易感者,即尚未感染疾病的人口数量;I 代表感染者;R 代表移出者,即已痊愈且产生免疫能力,或因病去世的人群。模型将考查不同房间的流动率,每个房间通过常微分方程进行编写。流动情况一般如下所示:

在 COMSOL Multiphysics 中,您可以输入任意代数或微分方程并求解。我们将在 COMSOL Multiphysics 中通过 SIR 模型来计算一个简单示例,比如说,冬季月份的流感。
如何在 COMSOL Multiphysics 中执行 SIR 模型
我们用到了全局常微分和微分代数方程接口,这也是 COMSOL Multiphysics 的核心功能之一。假设有一个总人数为 1000 的大学或公司,人群内的相互接触较频繁。整体环境相对孤立,也就是说,没有新人进入,大家的相互接触主要发生在组织内部。仿真开始时,一个人感染感冒,其他 999 个人很健康但属于易感人群。
我们可以假定在流感季的高峰到来时,感染者每天将传染其他五人。人们一般会在生病一到三天后决定回家休息。因此,我们假设每天移除 1/3 的感染者。我们将在 COMSOL Multiphysics 中输入 SIR 模型的所有方程组,求解它们在 30 天中的变化,然后分析结果。
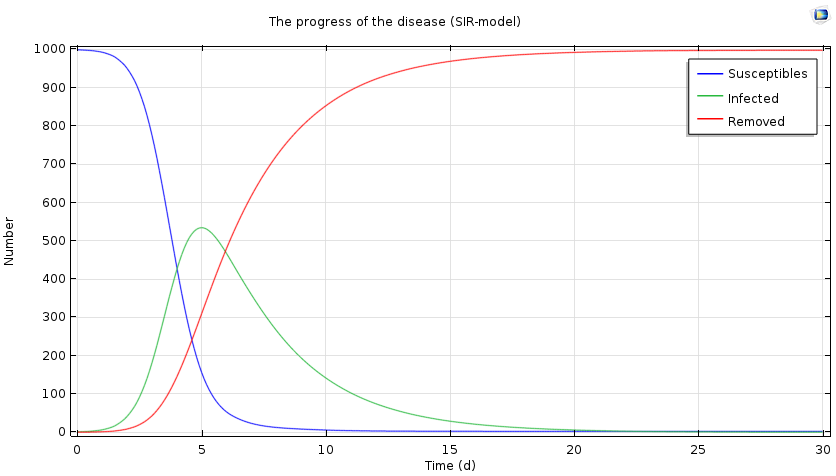
利用 SIR 模型得到流行病在 30 天中的发展情况。
我们可以看到一个特征阈值行为:如果第二批感染者的人数足够多,流行病就将爆发,患病人数将增加。同时,易感者的人数将减少,最终感染者将减少并接近零。上例中,疫情会在五天后达到高潮,一半的人群会被感染。
阈值行为由所谓的基本传染数控制,即接触率与复原率的比值,这是一个适用于所有疾病的基本量。但我们无法先验地确定该数目,因为它会受许多因素的影响,比如个体是否对疾病免疫以及多少个体会相互接触。这也使数理流行病学变得非常复杂,它是一个涉及医学、计算、统计、人口学、社会科学、生物、政治及经济的交叉学科。
我们再来分析如果每天 80% 而非 1/3 的感染者选择在家休息,那将得到:
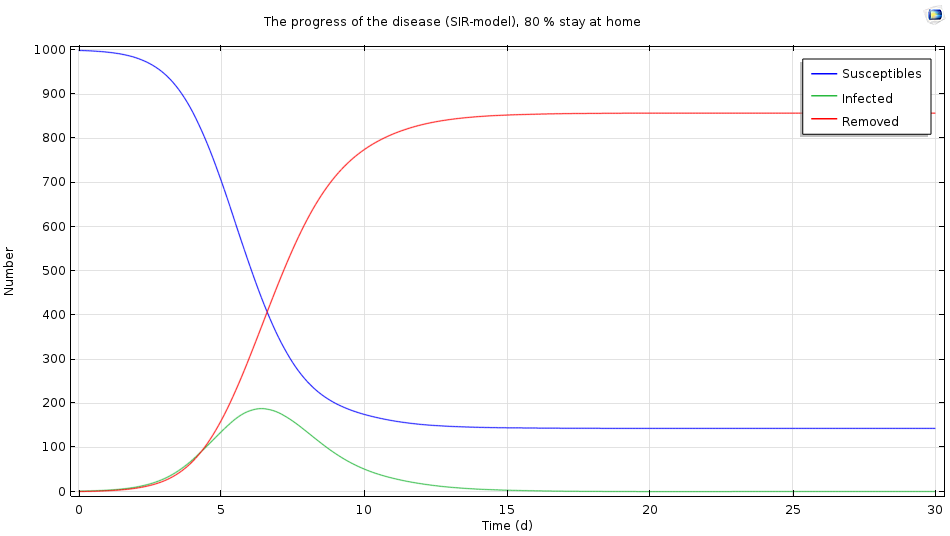
当 80% 的感染者选择在家休息时的仿真结果。
我们可以看到流行病的发展要平和一些:它在第六天达到顶峰,但只有不到 200 人感染。此时,感染后待在家会是正确的做法。
SIR 模型也有缺点:考察人群要足够大,不支持考察个体情况,而且人口应经过充分的融合。即便如此,研究人员还是能得出一些重要的结论,比如可以推导出对应的控制机制,应通过接种疫苗减少易感者数目,还是通过隔离减少接触率。
SIR 模型可以用于病毒性疾病,比如麻疹、水痘和流感。还有其他一些房室模型:SIS 模型会将所有感染者加到易感人群中(适用于常见的感冒)、SEIR 及 SEIS 模型会加入潜伏期或暴露时间。还有一些模型描述了病人无法完全康复或将转为携带者的情况,比如肺结核。
这些模型也存在一些缺点,但可用于对初始数据或假设进行定性验证。通过观察上图并与一些真实示例进行对比,我们发现二者之间存在偏差。也许我们的人群并非如此孤立,因为每位雇员还会与组织外的其他人接触;也可能存在潜伏期,或者其他人可能已经打了流感疫苗;也许还存在一些传播矢量,比如鼠疫中的老鼠。Eyam 村就发生了两波疫情,因此无法使用简单的 SIR 模型。
传染数也可能不同。例如,每天只有三或四个人感染。通过对比模型结果与真实数据得到传染数,并用于预测当疾病不在局限于地方性疾病时,应对多少人进行免疫。您可以在维基页面找到一些传染数。例如,模型显示应对超过 94.4% 的人群接种疫苗来根除麻疹。天花的传染数较小,约为 86%,这也是人们选择在全球根除天花的原因。
借助传热方程模拟流行病
在 COMSOL 用户年会 2010 收到的论文”借助持续监控数据模拟流行病的传播“中,Liang、Shi、Sritharan 和 Wan 用了另一种方法来模拟流行病。考虑到流行病的传播类似于传热与传质现象,他们使用传热模块和传热方程编写了一个扩散模型,用于模拟疾病在地理上的扩散。
流行疾病的扩散与人群的移动与人际接触相关,很像电子的运动及原子晶格振动。他们选择明尼阿波利斯作为样品城市,根据城市人口、交通网络结构及人口分布等地理信息来定义热方程中的介质属性;并将持续监控数据作为瞬态仿真的初始条件。在模型中,人口密度对应于材料密度;感染人数和恢复人数分别对应于热源和热损;接触率与传热速率相关。研究人员还借助传热模块的一些边界条件来提高建模效率,比如使用高导热薄层来定义当地的公路、高速及铁路。
论文作者们简要介绍了如何通过概率对流行病的传播进行随机描述。研究人员和公共卫生官员可以根据仿真结果设计公共预防及治疗策略。我们还可以通过其他方法来模拟延迟和其他随机微分方程,甚至能通过更复杂的模型考察每个个体、人际接触以及社交网络等因素,比如 Danon 等人的论文”传染病的网络及流行病学“。
仿真的力量:相同方程组的不同应用
我们可以在完全不同的自然或社会现象中应用相同的数学及物理模型,虽然这一点很让人吃惊,但它也促进了计算科学在多个全新领域的发展。上述 SIR 模型类似于Lotka-Volterra 方程组,后者描述了捕食者和猎物之间的动态关系。美国数学家 Richard Goodwin 将相同模型用于经济学研究,用于描述经济周期的动态变化,以及薪资与失业率之间的关系。
Liang、Shi、Sritharan 和 Wan 等研究人员还在他们的论文中提到,传热方程及其通用框架还可以用于预测蝗虫群的迁徙,并能模拟森林火灾的蔓延。传热方程也可以用于模拟金融数学及股市。科学家们甚至开发了其他物理模型来模拟金融市场的相变理论、流体动力学和统计物理学。
人们还将这类仿真用在了更多的研究应用中,包括舆论传播、语言演化、交通堵塞,甚至用于避税、社会隔离及武装冲突等领域。基于数学和物理的模型可以帮助理解及求解其他复杂问题,除技术领域外,还可以用于社会研究,特别是很难或无法通过测量或观察预测的问题。当仿真用于分析疾病的传播时,它最终将能帮助拯救无数的生命。
扩展阅读
- 深入学习利用 COMSOL Multiphysics 进行基于方程的建模:
- 查看 3 个基于方程建模的案例
- 阅读了解如何借助基于方程的建模理解交通拥堵
- 研究传热模块
- 学习如何利用 COMSOL Multiphysics 的 CFD 建模帮助预防感染
- 阅读一篇有关在网络中执行流行病仿真的综述论文:Leon Danon, Ashley P. Ford, Thomas House, et al., “Networks and the Epidemiology of Infectious Disease,” Interdisciplinary Perspectives on Infectious Diseases, vol. 2011, Article ID 284909, 28 pages, 2011. doi:10.1155/2011/284909






评论 (0)