
今天,来自 COMSOL 认证顾问 Lightness by Design 公司的特邀博主 Björn Fallqvist 讨论了如何使用仿真深入了解细胞的力学行为。
我们都知道,生物细胞是生命所必需的。它们不仅以 DNA 的形式存储和复制遗传信息,在生物过程中也起着重要作用。在大多数这些过程中,细胞的力学行为是确保正常生理功能的主要因素。
生物细胞的重要性
不言而喻,如果没有细胞,我们就不会存在或正常运行。脊椎动物利用红细胞的循环,即红血球向身体组织输送氧气。成纤维细胞利用它们的收缩机制迁移到伤口,并开始愈合过程。我们血管中的内皮细胞充当着过滤屏障,这些细胞不仅依靠生化/运输机制,还依赖它们的力学行为来确保正常的生理功能。
负责细胞硬度的结构性实体是一个被称为细胞骨架的相互连接的网络,如下图所示。这种细胞骨架主要由三种类型的聚合丝组成,每一种都有自己独特的结构和力学特性:
- 肌动蛋白
- 中间丝
- 微管
这种复杂的基础为细胞提供了即时和随时间调整其力学特性以适应环境的能力。
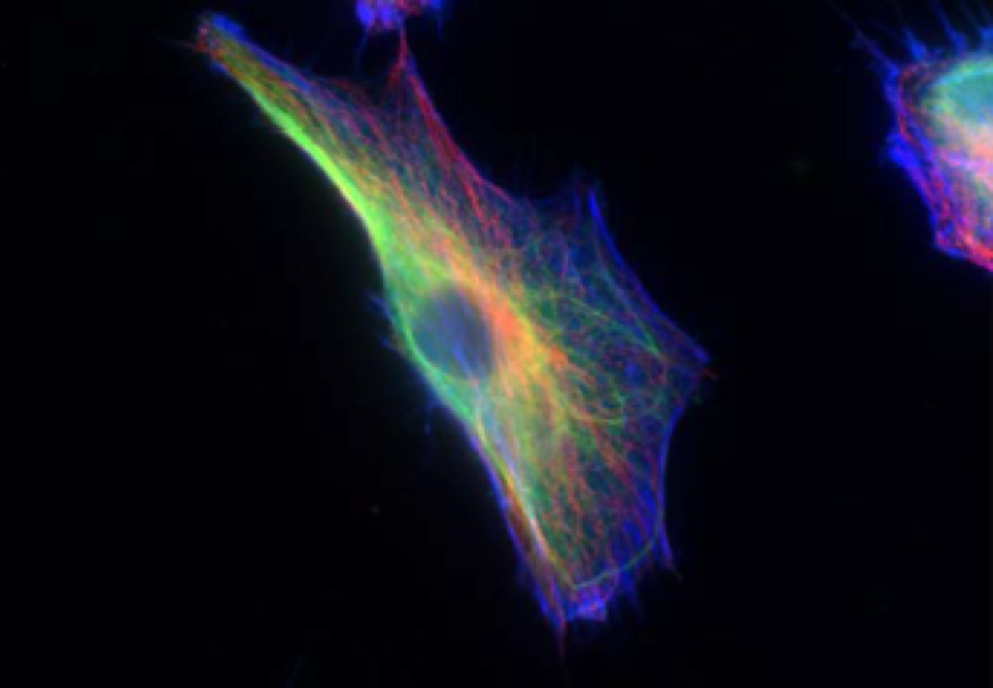
可以看见细胞骨架的成纤维细胞,包括肌动蛋白(蓝色)、中间丝(绿色)和微管(红色)。图片来源于论文 “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”, 经 Rathje 等人许可使用。
如以下通过原子力显微镜(AFM)进行的细胞压痕实验的弛豫曲线图所示,细胞和细胞骨架网络都是高黏弹性的。
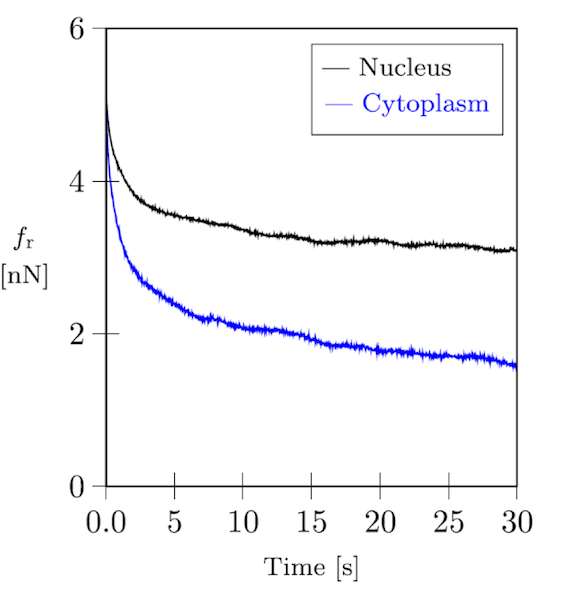
成纤维细胞的力松弛曲线。
大量的例子表明,患病的细胞表现出异常的力学特性,这促进了病理学的发展。在这些细胞中发现的细胞骨架与健康细胞相比,往往表现出不同的行为。例如,与对照组细胞相比,癌细胞表现出明显的硬度变化。在许多情况下,这可能与细胞骨架有关。中间丝网络可能在细胞核周围塌陷,或者细胞扩散增加(通过黏着斑与肌动蛋白细胞骨架紧密相连)。
研究细丝和细胞的力学行为
如前所述,细胞骨架是一个动态实体,具有在几毫秒到几小时的时间尺度上重塑自身的能力。由于它能组成网络,所以会产生明显的黏弹性行为。例如,肌动蛋白丝的溶液在短时间尺度上表现为固体,在较长时间尺度下表现为液体。这是由于半柔性长丝的热波动与其相互滑动的倾向之间的联系;也就是说,它们在短时间尺度上或多或少受到运动学约束。温度也是一个重要因素,部分是因为它影响热行为,还因为能连接溶液中的各种蛋白。
综上所述,很明显对这类底层聚合物网络的力学行为,以及其他细胞成分(例如,细胞核和细胞膜)等所有因素进行详细分析几乎是不可能的。但是,可以通过在宏观层面上考虑细胞来规避这一难题并获得结果。
通过在 COMSOL Multiphysics® 软件中创建有限元模型,我们基本上可以忽略异质细胞内结构,而是将其视为连续体;即,位移场是连续的。如果我们的目标是量化宏观细胞对外部刺激的反应,这是一个可接受的近似值。
本博客中描述的计算模型是松弛测试。测试过程为:将刚性压头压入柔软的黏弹性细胞中,测量由此产生的压头力松弛并与实验数据进行比较。
细胞的计算模型
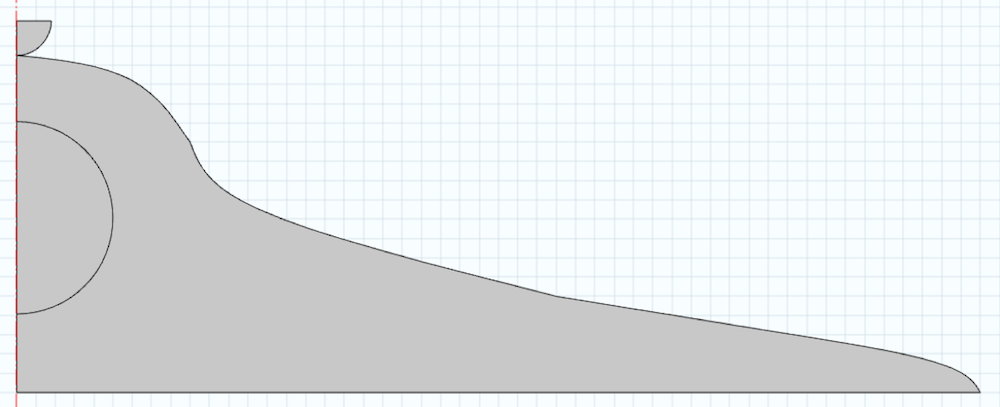
下面是一个典型尺寸的细胞模型。模型的域是围绕中心线创建的。半圆形的部分是细胞核,也会影响机械响应。我们还在几何形状中创建了一个压头,在分析中忽略了细胞膜。为了简单起见,我们假设细胞是轴对称,进行二维分析。
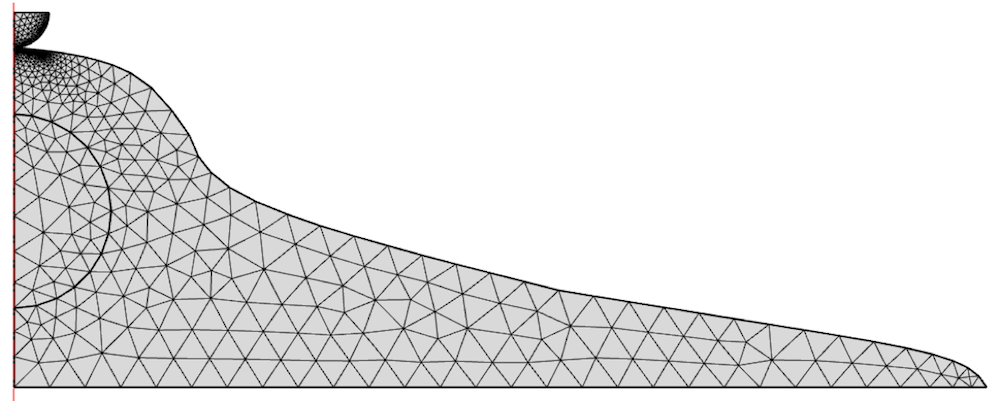
该模型使用二维单元网格进行划分,并在压头下进行了细化。
细胞质和细胞核材料模型的选择应该同时反映材料的瞬时和长期响应。线性弹性模型太简单了,因为细胞通常可以承受大的应变,并表现出明显的应变硬化。对于细胞质的响应,我们可以选择一个简单的超弹性材料模型,即 neo-Hookean 模型,其中应力和应变是由应变能量密度函数 Ψ 计算出来的,其形式为
{I}_1-3)+{\frac{\kappa}{2}}〖(J_el-1)〗^2
在这种形式中,假定材料(几乎)不可压缩,剪切模量 μ、弹性体积比 Jel、体积模量 κ 和等容第一不变量 \overline{I}_1 被包含在内。为了结合黏弹性行为,还包括两个广义麦克斯韦节点。已发现细胞核主要是弹性的,因此在建模时没有使用黏弹性节点。
所选材料参数如下表所示:
| 域 | 剪切模量 | 体积模量 | 能量因子 1 | 松弛时间 1 | 能量因子 2 | 松弛时间 2 |
|---|---|---|---|---|---|---|
| 细胞核 | 1.667 kPa | 5000 kPa | N/A | N/A | N/A | N/A |
| 细胞质 | 0.155 kPa | 1000 kPa | 10 | 0.5 s | 10 | 50 s |
细胞的底部受到垂直约束。虽然在现实中,细胞通过黏着斑黏附在基板上,但这应该是局部效应,不会显著影响机械响应。
压头和细胞之间的接触由罚公式强制执行,使用压头作为源边界。指定压头域的速度为 0.1 µm/s,直到总垂直位移为 4.6 µm。随后在分析中保持固定,总时间为 30 s。
仿真结果
受压后细胞的局部变形如下图所示。
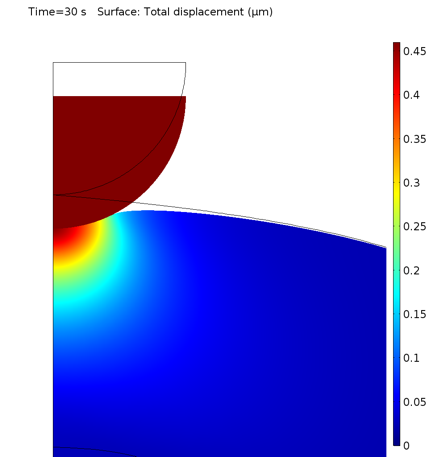
压头下的细胞变形。
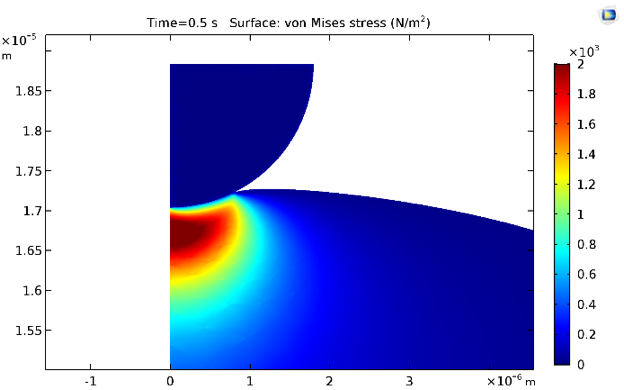
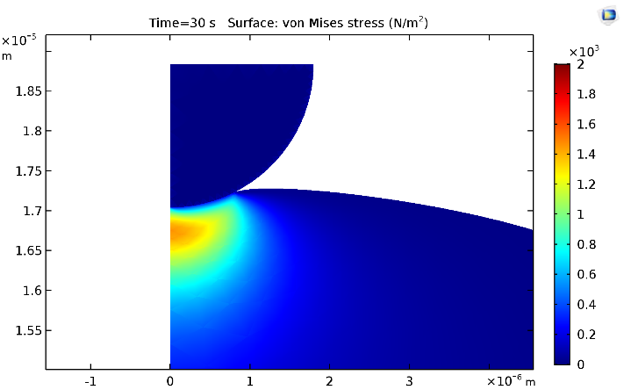
0.5 s 和 30 s 时的等效 von Mises 应力如下所示。很自然地,由于细胞质材料模型包含黏弹性分支,应力因应力松弛而降低。
0.5 s(左)和 30 s(右)时的应力分布。
可以从 COMSOL Multiphysics 仿真结果中提取压头上的垂直反作用力,并与实验数据进行比较。
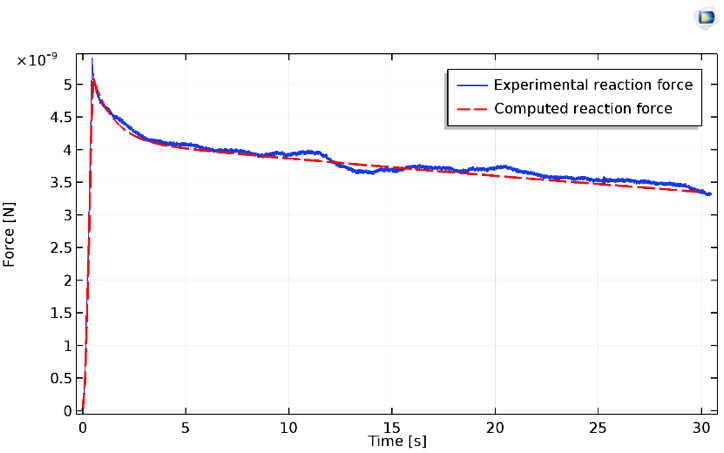
细胞受压力的结果,实验(蓝色)结果和计算(红色)结果。
通过实验测量的松弛,通常表现出至少两种不同的状态。这些值可以由简单的 neo-Hookean 模型以及它的两个黏弹性节点合理地预测出来。应该注意的是,在恒定斜率之前,初始受压状态表现出严重的应变硬化(在上图中很明显)。
关于生物力学仿真的最终想法
如前所述,COMSOL Multiphysics 可以很容易地通过(比较)简单的材料模型来复制细胞的黏弹性行为。自然地,也可以通过使用更复杂的材料模型来获得更高级别的复杂性。在这种情况下,使用其他超弹性模型,例如 Mooney-Rivlin 或 Ogden 模型,结合更多的黏弹性节点可能会产生更准确的结果。需要记住的是,由于需要更多的材料参数,因此必须为相关材料提供有更多的实验数据点。
实际上,细胞是一个比模拟的模型要复杂得多的系统。力学和生物化学信号的不断交换,不断改变着细胞内结构、细胞形状和运动行为。可以说,将细胞建模为一个连续体是一个主要的简化,这种近似值在许多情况下可以很好地为我们服务。例如,如果我们要分析转移的细胞,可能只需要描述它们的宏观硬度,用于评估它们挤压组织或动脉的能力。在这种情况下,与障碍物相比,细胞作为一个整体的刚度将是决定性的因素,而不是例如细胞骨架和细胞核这类详细的相互作用。
还应该提到的是,细胞不仅是一个复杂的系统,而且远不是确定性的,也不是由一组几何和材料参数唯一表征的。单个细胞之间的反应取决于它们的健康状况、运动状态和细胞周期状态等因素。为了通过实验正确评估细胞的机械响应,需要探测更多的单个细胞。然而,我们建模时关注的是评估对某一个单个细胞的响应进行建模。
通常,不仅细胞,其他生物材料也可以通过超弹性材料模型来仿真。根据特定的材料和时间尺度,还可以包括黏弹性行为。这为生物力学建模领域开辟了一些有趣的机会。
例如,动脉粥样硬化是一种常见的心血管疾病,白细胞积聚在动脉壁上,减少血流量并增加因血栓而心脏病发作的风险。缓解这种情况的常用方法是采用血管成形术,即将球囊插入动脉并充气,然后使用机械支架来稳定动脉部分。使用 COMSOL Multiphysics,我们可以捕捉动脉壁的超弹性-黏弹性行为,以及由胶原纤维方向引起的复合特性,并计算应力和应变的瞬时和瞬态发展。
2018 年 8 月 20 日,编者注:相应的细胞松弛模型文件已添加到 COMSOL 模型交流页面。您可以点击此处查看。
关于作者
Björn Fallqvist 是 Lightness by Design 的一名顾问,从事基于数值分析的产品开发工作。他于 2016 年从皇家理工学院获得博士学位,致力于开发本构模型以捕捉生物细胞的力学行为。他的主要专业兴趣和专长是材料表征领域和使用各种材料模型来捕捉物理现象。
参考文献
- Rathje et al, “Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness”, Proceedings of the National Academy of Sciences, 111, pp. 1515–1520, 2014.
- B. Fallqvist et al., “Experimental and computational assessment of F-actin influence in regulating cellular stiffness and relaxation behaviour of fibroblasts”, Journal of the Mechanical Behavior of Biomedical Materials, Vol 59, pp. 168–184, 2016.






评论 (2)
岱言 蒋
2025-09-13对于comsol6.2来说,您的模型好像已经不适配新的软件
Liwen Yang
2025-09-16 COMSOL 员工您单击一下 “组件:2D cell” 设置中的 “永久定义所有坐标系”、将其取消,即可在6.2中计算该模型。