
惯性聚焦是一种有用的技术,可用于各种应用,特别是在医疗领域。确保该技术的有效性,需要准确描述粒子在流经通道时的迁移情况。COMSOL Multiphysics® 软件 5.3 版本中提供了一个新的基准模型工具,可生成与惯性聚焦实验数据一致的可靠结果。
惯性聚焦的力量
1960 年代,G.Segré 和 A.Silberberg 发现了一个令人惊讶的效应。通过层流管道的中性悬浮粒子会聚集成一个环状结构,其半径约为管道半径的 0.6 倍,位于距平行壁约 0.2 倍通道宽度的距离。正如他们在几十年后发现的那样,发生这种行为的原因可以追溯到惯性流中作用于粒子的力。
今天,我们用惯性聚焦这个术语来描述粒子向平衡位置的迁移。这项技术被广泛用于临床和医疗点诊断,作为一种聚集和分离不同大小的粒子以进一步分析和测试的方式。
许多类型的医疗诊断都使用惯性聚焦进行测试和分析。图片在公共领域,通过 Wikimedia Commons 获得许可。
为了使惯性聚焦在这些和其他应用中有效,准确分析粒子的迁移模式是一个关键步骤。COMSOL Multiphysics 最新 5.3 版本中提供了的一个新的基准例子,强调了为什么 COMSOL® 软件是获得可靠结果的正确工具。
准确模拟惯性聚焦中粒子的迁移
这个基准示例中,以一个二维泊肃叶流中的粒子轨迹为例来说明。为了说明相关的力,我们使用了来自两个平行壁中的流体速度呈二维抛物线分布的粒子的类似迁移表达式(见模型文件中的参考文献2)。COMSOL 中内置的升力和曳力修正使我们能够在模拟分析中考虑到这些壁的存在。
注:升力和曳力构成了作用在蠕动流内的中性悬浮粒子上的总力。根据定义,重力和浮力相互抵消。
我们假设升力只在垂直于流体速度的方向上,还假设球形粒子与通道的宽度相比很小,并且它们是刚性旋转的。
为了计算速度场,我们使用了层流 物理场接口。然后通过曳力 节点将其与流体流动颗粒跟踪 接口耦合起来。通过层流流入 边界条件,我们可以自动计算出入口边界的完整速度分布。对于两个平行壁内的牛顿流体层流,速度分布将呈抛物线。这意味着我们可以直接输入流体速度的解析表达式。然而,在这个例子中,我们选择使用了层流 物理场接口,因为它展示了最适合于一般几何结构的工作流程。
我们来看看模拟结果。首先,我们可以看一下通道中的流体速度大小。正如预期的那样,速度曲线是呈抛物线分布。请注意,这个几何体的长宽比是 1000:1,所以通道与它的高度相比是很长的。该图使用了一个自动的视图比例,使结果更容易被展示。
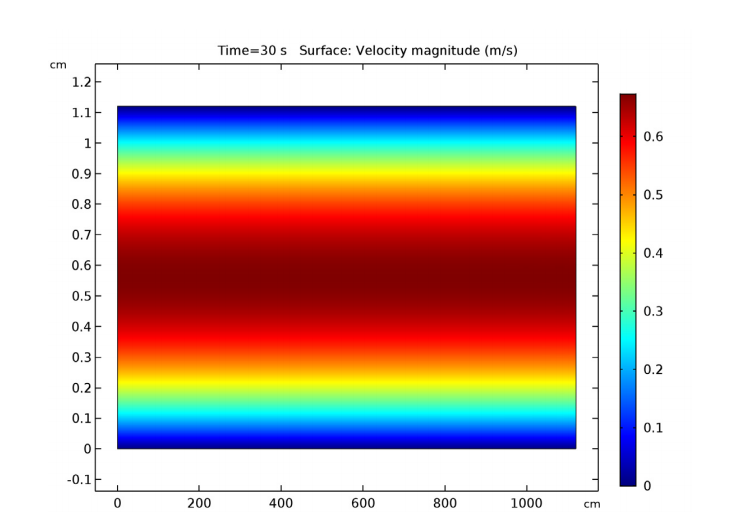
一个由两面平行壁约束的通道内的抛物线型流体速度曲线。
然后,我们可以把注意力转移到中性悬浮粒子的轨迹上。请注意,在下面的图中,颜色表达代表粒子速度的 y 分量,单位是 mm/s。结果表明,在通道中心两侧约 0.3D 的距离上,所有的粒子都接近于平衡位置。(D 代表通道的宽度)。然而,在通道中心附近释放的粒子确实需要更长的时间来到达这些位置。这些例子的初始力较弱,因为它们被释放在速度梯度最小的区域。从图中,我们可以看到,粒子在通道宽度的 0.2 和 0.8 倍的高度上聚集。这些发现与实验观察结果显示出良好的一致性。
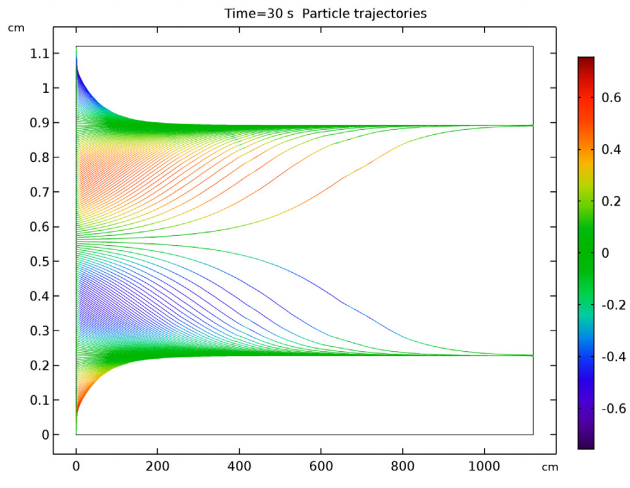
管道内部的粒子轨迹
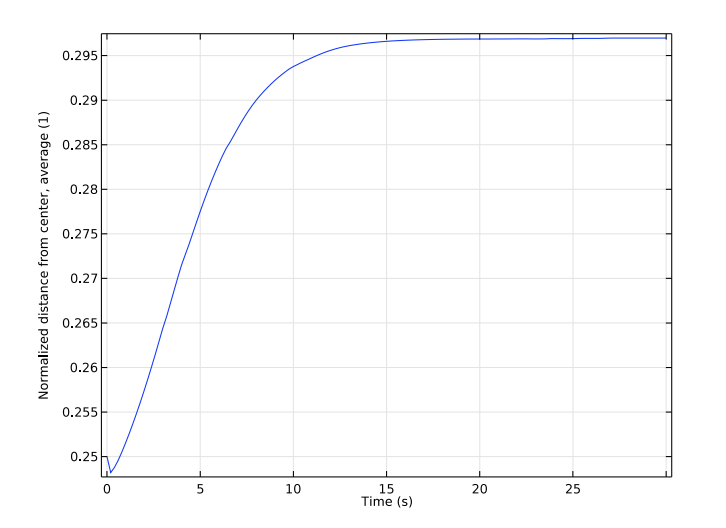
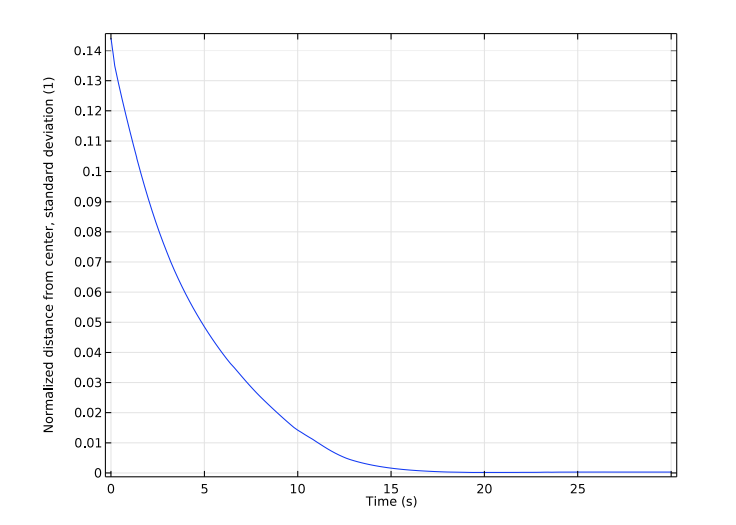
最后两幅图显示了粒子与通道中心之间归一化距离的平均值和标准偏差。这些结果验证了与通道中心的平衡距离实际上是在 0.3D 左右。
粒子与通道中心的归一化距离的平均值(左)和标准偏差(右)。
仿真为惯性聚焦研究生成可靠的结果
为了有效地将惯性聚焦用于医学和其他应用,需要首先了解粒子在通过通道迁移到平衡位置时的行为。利用 COMSOL Multiphysics® 5.3 版本,可以进行这些研究并产生可靠的结果。这种对惯性聚焦的准确描述是分析和优化依赖这种技术的设计的基础。
如果您对此感兴趣,欢迎自己动手尝试模拟我们的新基准模型。
您是否有兴趣了解 COMSOL Multiphysics 5.3 版本的进一步更新?您可以在我们的 5.3 版本发布亮点中获得全部信息。






评论 (0)