电磁学 博客文章

计算电动机的损耗、温度和效率
跟随我们研究铁损和铜损的变化、由此产生的温升及其对永磁电机效率的影响。

如何对卷绕和翘曲几何形状进行建模?
CAD 零件通常设计为未变形的制造状态。 然而,当谈到分析时,我们只对变形的组装状态感兴趣。
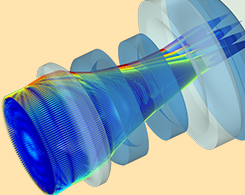
通过仿真优化微型相机模组设计
灯光、相机、模拟:了解有助于定义紧凑型相机模块 (CCM) 性能的因素,以及如何使用光线追踪来分析其设计。

设计用于红外应用的抗反射微结构
探索 2 种微结构设计如何在特定波长光谱内将硅 (~70%) 和碲化镉锌 (~79%) 的体透射率提高到 90% 以上。
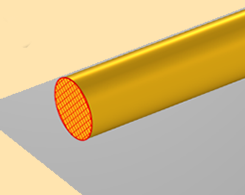
模拟波状电磁场中的电压和接地
我们通过定义和解释正弦时变模型的这些术语来继续讨论电压和接地。
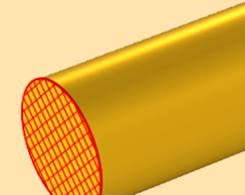
电压和接地是否存在?
当我在大学学习电气工程类课程时,我真的希望当时学习的一些知识能换种方式教授。例如,电压 和 接地 的概念就属于这一类知识,因为这些术语经常会在不易察觉的情况下被误用。

COMSOL Multiphysics® 在生物医学领域的 8 种应用
从机械心脏泵植入物、疫苗存储装置到血液分析仪,生物医学应用本质上通常是多物理场。因此,多物理场仿真可以帮助从根本上改变生物医学设备和流程的设计和分析方式。今天这篇博客,我们分享了 8 个真实的例子,来介绍生物医学领域的工程师和研究人员如何使用 COMSOL Multiphysics® 软件驱动他们创新的救生设计。 1. 左心室辅助装置 心脏衰竭,或称充血性心力衰竭,仅在美国就影响了超过 600 万成年人。当心脏不能向全身输送足够的血液和氧气时,就会发生这种常见的疾病。帮助缓解心力衰竭的一种方法是使用左心室辅助装置(LVAD),这是一种机械泵,植入胸腔后可提供循环支持。左心室辅助装置通常被称为 “移植的桥梁”,因为它们通常用于治疗等待心脏移植的病人。不仅如此,它们也可以被用作因客观医疗条件而无法接受心脏移植的病人的长期治疗方案。 正如预期的那样,左心室辅助装置的设计通常很复杂。他们需要: 足够的功率(大约10 瓦左右),可以正常运行 足够小,可以装进病人的胸膛 由与人体相容的材料制成 为了设计具备所有这些品质的左心室辅助装置,雅培实验室的研究人员使用了仿真技术。例如,他们使用 COMSOL Multiphysics 帮助设计了左心室辅助装置的离心泵。为了防止血液在泵内和泵周围凝结(设计 左心室辅助装置 时的一个常见挑战),研究人员在 左心室辅助装置 的设计中加入了一个磁悬浮转子。使用COMSOL,研究人员能够对 左心室辅助装置中的转子和湍流进行建模和分析。 磁悬浮转子的仿真(左上),泵腔内流体流动的 CFD 仿真(左下),以及 左心室辅助装置 的离心泵示意图(右)。 此外,研究人员还对左心室辅助装置的控制器进行了机械冲击分析,用于研究它的弹性。这个控制器有助于左心室辅助装置的供电、控制和性能监控。 “我每天都在使用 COMSOL Multiphysics,包括概念验证模型和模拟非常复杂的、具有详细 CAD 几何结构和多种相互作用的物理特性。我花费了数个月在一些复杂模型上以获得我所有需要的信息。” – Freddy Hansen, 雅培实验室高级研发工程师 2. 疫苗储存 根据美国疾病控制和预防中心的说法,疫苗储存在减轻常见可预防疾病的传播方面发挥着重要作用。然而,由于严格的温度要求,许多疫苗在存储过程中会变质,从而造成浪费。 作为全球公益项目的一部分,Intellectual Ventures 公司创新设计了一种被动式疫苗储存装置,用于将疫苗安全地运送到世界各地。它的设计只需要使用一批冰就可以将疫苗保持在 0°C~10°C。它的外壳具有多层绝缘,包括反射铝薄层、低导电空间和非导电真空空间。被动式疫苗储存装置不需要外部电源就可以工作。 在 COMSOL Multiphysics 中进行的被动式疫苗储存装置热仿真。 在设计阶段,研究人员在一个与撒哈拉以南非洲地区温度相似的环境室中测试了几个被动式疫苗储存装置原型的性能。为了优化被动式疫苗储存装置系统的设计,在建造原型之前,该团队使用了 COMSOL Multiphysics 以及它附加的各种产品,包括传热模块和分子流模块。 通过实验和模拟,该团队能够设计出一种容易运输的被动式疫苗储存装置,可以将疫苗冷藏长达一个月,从而能够将疫苗安全运输到世界各地,甚至是在电力有限或没有电的地方。 3. 消融技术 2020 年,肝癌是全球癌症相关死亡的第三大常见原因,导致了超过 80 万人丧生。这种疾病有时用消融技术进行治疗。这是一种微创治疗,可以在不切除肝脏肿瘤的情况下破坏它们。治疗肝癌的两种消融术包括: 射频消融 (RF),使用针状探针传递高频电流来加热和杀死肿瘤内的癌细胞 微波消融 (MW),使用针状探针发送电磁波来破坏肿瘤内的癌细胞 许多执行这类消融治疗的医疗专业人员面临的一个共同挑战是,他们无法获得有关这些程序有效性的实时反馈。为了解决这各问题,射频和微波消融技术的领先开发商——美敦力公司的一个研究团队使用仿真设计了具有更强的可预测性和有效性的新型消融探针。在他们的工作中,该团队使用 COMSOL Multiphysics 和附加的射频模块来优化探头的发射和接收特性。 4.老花眼 随着年龄的增长,我们的眼睛会出现越来越难以聚焦近距离的物体的情况。这种情况被称为老花眼,会影响到世界上大多数年龄到了65岁的人。老花眼的主要原因是晶状体形状的变化,晶状体是眼睛内部的一个微小结构。在我们年轻的时候,晶状体很薄且有弹性,但随着时间的推移,它会逐渐变厚,弹性变差。如果不加以矫正,老花眼会是造成视力障碍的最常见原因。 老花眼可以通过使用眼镜、隐形眼镜或简单的放大镜来缓解。一种更深入的治疗形式是屈光手术。但是,所有这些选择都有其自身的缺点和限制。 用于帮助研究老花眼的人眼模型。 为了推进老花眼的研究并治疗老花眼的根本原因,瑞士医疗器械公司 Kejako 的研究人员创建了一个人眼的 3D 机械模型。使用 […]
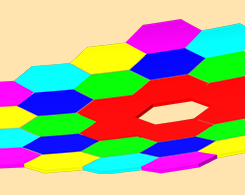
对清晰度的追求:在 3 种望远镜设计中追踪射线
凯克望远镜包括一个由 36 个独立的互锁镜组成的抛物线反射面。 通过光线追踪模拟了解更多关于这个和其他 2 个流行望远镜设计的信息。



