通用 博客文章

如何在 COMSOL Multiphysics® 中进行多种材料优化
用铝而不是铜或钢制成的音叉听起来会更好吗? 在 COMSOL Multiphysics® 中,您可以对多种材料进行优化研究以找出答案。

如何使用参数估计研究步骤进行逆向建模
创建仿真时,通常首先从构建正向模型开始,设定各种输入值,然后查看结果。但是,如果我们已经通过实验或调查得到一组结果(如材料属性),然后想通过仿真找到能得出相同结果的输入数据,该怎么办?本篇博文,我们将通过一个视频教程向您演示如何在 COMSOL Multiphysics® 中使用 参数估计 研究步骤帮助我们建立逆向模型,并求解模型的最佳输入值。 视频教程:在 COMSOL Multiphysics® 中执行参数估计研究 使用参数估计研究步骤进行逆建模 假设我们需要通过仿真得到有一组外部数据(来自实验测量值或参考数据集),我们该怎么做?这时,我们可以使用逆向建模 。顾名思义,逆向建模就是对问题采取逆向建模的方法,即求解的不是输出值,而是输入参数。 为了获得所需的仿真结果,我们可能需要调查或通过实验得到几种模型输入值,例如材料属性。在求解这些输入值时,为了使外部数据和仿真结果非常接近,我们会寻找最优值。很自然,我们想到了使数据之间差值的平方和最小的方法来求解。因此,将问题构建为最小二乘优化问题是一个有效的建模策略。为了简化设置和求解问题的过程,我们可以使用 COMSOL Multiphysics® 软件中的参数估计 研究步骤。 注意:要使用 参数估计 研究步骤,研究的问题必须与时间有关,并且需要具有COMSOL 软件优化模块的许可证。另外,还需要通过一个插值函数或用户定义的参考表达式来引入一组参考数据。请注意,参考数据必须是与时间相关或者是一个单变量函数。 参数估计研究步骤的 “设置”窗口。 参数估计 研究步骤对于各种逆向建模问题(主要是参数估计)非常有用,其目的是估计模型所需输入(即参数)的值,这可以帮助我们深入了解参数的数值大小(以及属性)影响目标函数的方式。 参数估计 功能最典型的用途之一可能是曲线拟合或类似的数据拟合应用。此过程涉及将函数拟合到一系列数据点。函数的拟合是通过估算函数中的系数值来完成的,本质上是将参数化的解析函数拟合到一个数据集合。通过将曲线拟合到一组数据点,我们可以对函数以及无法得到确切数据的区域进行插值。 在本文开头的教程视频中,我们通过一个优化后的 弯头支架教程模型 演示了参数估计的使用。在进行这项研究之前,我们需要正确定义问题…… 在 COMSOL Multiphysics® 中执行参数估计研究 在 COMSOL 中执行参数估计研究通常包括三个主要步骤: 预研究:准备定义,例如参数、变量和函数 研究设置:自定义研究的各项内容并进行计算 后期研究:进行后期处理使结果可视化,比较模拟值和实验结果,并提取最佳的参数估计值 下面,让我们看一下如何完成这些步骤,以及在模型中设置 参数估计 研究步骤时需要考虑的重要因素。 步骤 1:参数估计预定义 在进行参数估计研究之前,我们必须先定义问题。这通常涉及创建参数、函数和变量的组合。首先,我们定义模型的输入参数,它们是需要被估算的值;接下来,通过定义一个参考函数或表达式来引入外部数据;最后,定义一个从仿真结果中提取并评估的输出变量,并将其与测量得到的输出数据进行比较。 在文中开头的视频中,我们对弯头支架进行了瞬态传热分析。然后将传热仿真得到的模拟数据与实验数据进行了比较,该实验数据用于评估材料的热导率值。 在固体传热 节点中,导热系数用 k 表示。因此,我们定义一个名为 k 的参数,输入一个 k 的粗略估计值,并在适当的节点中用它来定义导热系数。 左:用于参数估计研究的参数,包括用于估计导热系数的参数 k。右:在节点(名为实体 1)使用参数 k 定义需要估计的材料属性。 接下来,为了将外部文件中的数据引入到 COMSOL® 软件中,我们创建了一个定义。在本例中,参考数据是一个与时间相关的温度测量值的集合,这些值包含在一个用逗号分隔(CSV)的文件中。通过将 插值 函数添加到模型组件中,然后使用从文件加载 按钮,可以快速轻松地将这些数据输入 COMSOL Multiphysics。数据以表格格式自动导入,第一列为时间,第二列为温度测量值。 通过“插值“ 函数将参考数据引入仿真中”从文件加载”按钮用于将外部文件导入函数。 在单位 部分,我们只需要简单的输入参数(时间)和函数(温度)的相应单位,无需设置函数的 插值和外推 选项,因为研究仅计算函数的自变量或 t 列中明确指定时间点的差值。因此,数据点之间的平滑度和超出数据范围的函数行为设置并不重要。 现在,我们需要定义一个表达式,以从仿真结果中提取温度量(此量随后将与内插函数中的温度测量值进行比较)。我们要提取并用于比较的量是支架右上端表面的平均温度。 由于要获取量(温度)的平均值,因此我们首先在 […]
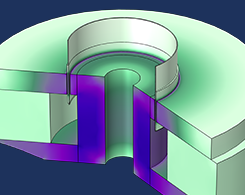
扬声器中磁路的拓扑优化
今天的消费者需要既精致又轻便的扬声器。 拓扑优化可帮助工程师设计实现此目标的组件。

主题演讲视频:超越传统仿真的生物制药App
Amgen 公司的 Pablo Rolandi 在 COMSOL 用户年会 2017 波士顿站上发表了主题演讲,讲解 Amgen 如何在生物制药开发中超越传统的建模和仿真。Rolandi 分享了五个例子来说明这一理念在生物和合成医学中的应用。如果你错过了他的演讲,可以在此观看视频录像,并阅读他讨论的亮点内容。

如何使用插值材料数据模拟不规则几何
在上一篇博客文章中,我们讨论了创建不规则形状的几何图形的不同方法。本篇博客文章中,我们将通过使用插值函数演示一种非常强大的替代建模方法:利用拟研究对象材料属性的空间变化间接定义不规则形状,来代替创建几何对象。

COMSOL Desktop® 环境如何实现在集群上运行
在高性能计算(HPC)硬件上运行 COMSOL Multiphysics® 软件对许多类型的分析都非常有利,这是创建集群计算 节点的主要原因之一,该节点有助于将 COMSOL® 软件与任何类型的 HPC 基础设施无缝集成,同时保持图形用户界面的便利性。在本篇博客文章中,我们将学习如何直接从 COMSOL Desktop® 图形环境在 HPC 硬件上远程运行大型仿真。

借助分步仿真优化增材制造工艺
增材制造有着广泛的应用,例如制造定制医疗设备、航空航天器材和艺术品。随着潜在用途的不断增加,增材制造能够满足需求是非常重要的。然而,分析和优化这个复杂的过程可能很困难。工程技术人员能做哪些工作来克服这个挑战呢?

含热粘性损耗的声学拓扑优化
来自丹麦 GN Hearing 公司的特邀博主探讨了如何在助听器、手机和超材料几何结构等微型声学装备的拓扑优化中加入热粘性损耗。



