化学反应动力学系列的最后两篇博客文章关注基于一组特定参数的化学反应的建模。尽管这一点很重要,学术界和工业界对此也很感兴趣,但通常在建模时,会假设相关参数的取值。现在,让我们了解如何使用 COMSOL Multiphysics 估算化学反应动力学参数。
化学反应参数
引用我的一位前教授最喜欢的一句话:“一位善良而仁慈的仙女挥舞着魔杖,并给了我们活化能。” 事实是,这些参数(速率常数,活化能和指前因子)是大量重复实验的结果。在我的研究生涯中,几乎所有的实验室工作都包含在不同温度下进行化学反应、定期采样、转换结果以及计算速率常数。
重氮化合物,危险爆炸性
我们来看一下化合物氯化重氮苯(BDC)的结构:
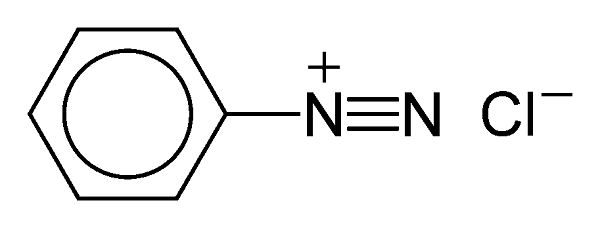
尽管这个小小的结构看起来无害,但它却充满了冲击力。它属于重氮化合物家族(意味着碳原子 C 与两个相连的氮 N 原子相邻),该类化合物是一组易燃易爆的危险性化合物。
BDC 何时分解?
回想一下本系列第一篇关于阿伦尼乌斯定律的博客文章中提到的:任何分子都需要特定数量的能量来克服其固有的“惰性”或对反应的抵抗力————这种反应就是活化能。今天,我将介绍如何通过一系列的实验(以及 COMSOL Multiphysics 的仿真模型)精确地优化出这种能量,从而能够对特定过程的安全性作出预测。
实验
BDC 的分解不可逆(如爆炸所预期的那样),因此我们可以写出相当简单的反应方程式:
BDC → 产品
对应的速率方程(相关详细信息,请参见“ 化学动力学通论,阿伦尼乌斯定律 ”):
(1)
与浓度相关的常微分方程(ODE):
(2)
如果我们回想起阿伦尼乌斯方程,
(3)
问题就会变得相对清楚了。通过在不同温度下进行分解反应并在不同时间测量 BDC 浓度,我们可以用模型中的常微分方程的解拟合出最能反映实验结果的 A 值和 E_\mathrm{A} 值。
当然,上述速率方程可以直接积分,而在试验数据处理时,我们将利用我们的浓度与时间表达式(我们在阿伦尼乌斯定律中得出过类似的表达式)从 \ln{c_\mathrm{BDC}} 对 t 的直线绘图梯度来确定速率常数。然后我们可以绘制 \ln k 对 1/T 的图以找到活化能,该过程可以看作是图形化最小二乘问题,因为实验点永远不会“完美”对齐。
本文中,我们将使用参数估计工具来演示如何获取上述简单过程的数值解。将自动参数估计用于化学机理研究时,该方法变得更有价值,因为我们不知道浓度随时间变化的函数的具体形式,因此必须构建模型。
在 COMSOL Multiphysics 中估算化学参数
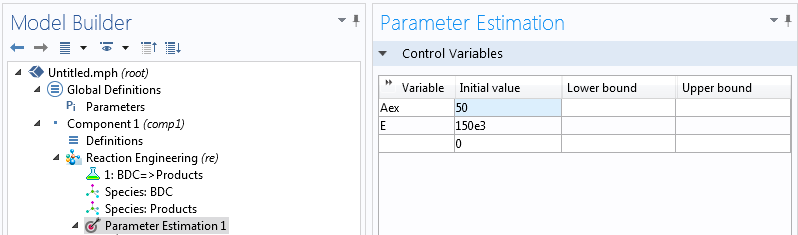
通过模型开发器,我们可以从模型向导中选择一个瞬态研究的 0 维反应工程接口。通过 BDC → 产物输入反应,并定义初始 BDC 浓度为 1mol/L。首先定义一个名为 “ Tiso” 的参数(用于系统温度),只需要简单的鼠标操作,就将该参数作为系统温度使用。通过右键单击反应工程节点,我们可以添加一个参数估计接口,在这里我们可以选择控制变量并定义最小二乘问题。
如果我们选择不针对 A 而是针对 eA 进行优化,则实际上可以大大减少计算量。这样,求解器可以同时处理两个指数型参数,而不是一个线性和一个指数型参数。合适的初始值取决于经验,大约 150kJ/mol 的活化能和大约 e50 的指前因子都是合理的。
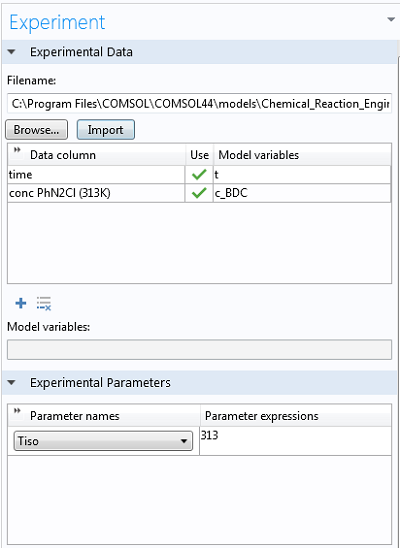
将实验数据导入 COMSOL Multiphysics® 非常简单,只需右键单击 Parameter Estimation,选择要从文件加载的选项,然后选择相应的 .csv 文件(这些文件可以很容易地从 Excel® 导出)即可。在实验设置窗口的底部,我们可以为不同温度的实验选择不同的实验参数。导入后会自动绘制数据,因此我们可以确保它是合理的:
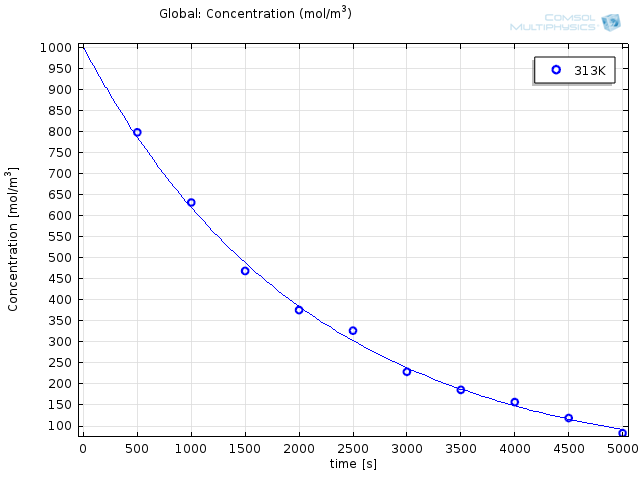
最后,我们可以从反应设置窗口中选择使用阿累尼乌斯表达式的选项,并输入控制变量名称(”exp(Aex)”表示前置因子,“E” 表示活化能)。通过选择介于 0 到 5000s之间的研究时间,我们确保考虑了所有实验数据。
选择正确的研究
在研究中选择求解器取决于目的,并且我们通常根据经验进行选择。对于反应工程的参数估计,Levenberg-Marquardt 求解器通常是最佳的选择,因为它在反应动力学的参数估计领域中已得到公认。虽然运行仿真仅需几秒钟,但结果却是惊人的:
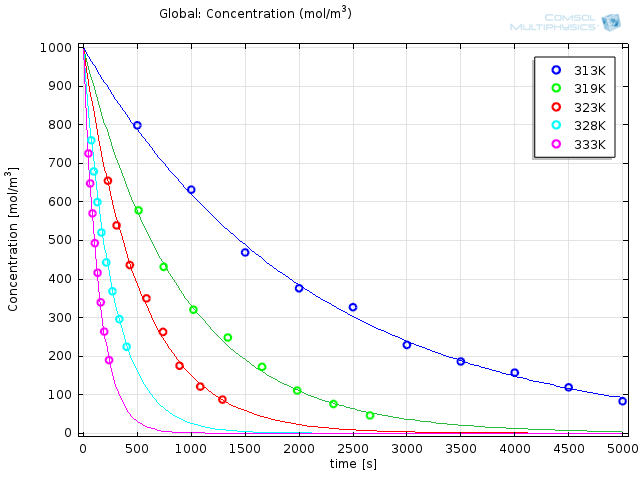
具有优化的反应参数(实线)和实验结果(o)的建模结果。
前置因子和能量的值分别为 e36.9s-1 和 116 kJ/mol。实验是非常棘手的过程,它需要耐心、精确和极大的勇气。而我们通过简单的将实验数据导入和插值,可以快速获取反应参数,从而将精力专注于其他真正重要的事情。
后续操作
化学动力学系列的下一篇博客文章将探讨如何将外部数据输入模型-热力学的插值函数方法。这将是化学工业中最引人入胜的过程之一。这里所说的化学反应,就像托尔斯泰的《战争与和平》所描写的历史那样,具有戏剧性和复杂性,敬请关注!



评论 (0)