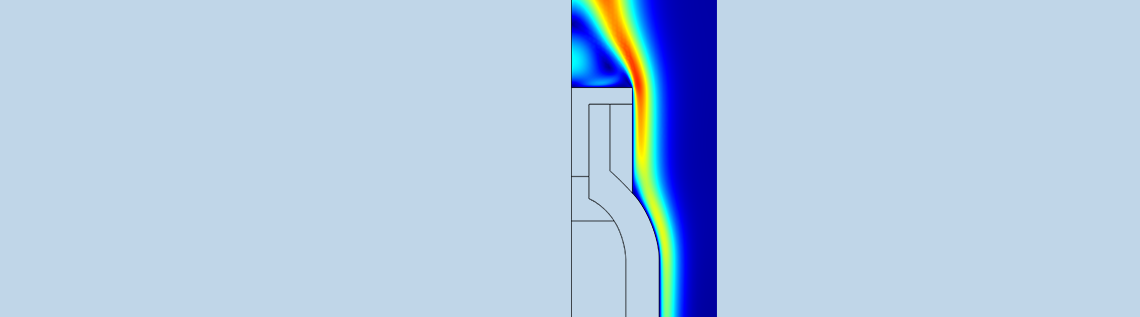
针对流体流动和温度场的数值分析可为很多工程应用提供有价值的参考。在执行此类仿真时,效率是一个重要的考虑因素。在本文中,我们将讨论 COMSOL Multiphysics® 仿真软件中多种形式的流体流动方程,以及这些方程中每个选项的最佳使用方式。同时还将着重探讨不同的选择对传热分析产生的影响。此外,我们还会介绍如何基于这些公式来创建自然对流和强制对流仿真。
COMSOL Multiphysics® 中 Navier-Stokes 方程的可压缩性选项
在分析某个流体系统的速度和压力场时,可能有多个方程形式适合描述该流体系统。举例来说,您采用达西定律可以足够描述多孔介质床层中流体的缓慢运动;但是一旦流体流动速度较快,便需要改用 Brinkman 方程。虽然可选方案很多,但今天我们将集中探讨 Navier-Stokes 方程,因为该方程是流体流动分析中最常用的方程。特别提示:本篇博客中的大部分解释和实践方法也适用于前文提及的方程。
第一步是基于流体密度对要模拟的流动类型进行表征。所有流体都是可压缩的,也就是说,流体的密度由绝对压力和温度决定,其热力学函数表达式为 \rho = \rho (pA,T)。然而,从实用性角度来看,只考虑温度便能实现对大多数流体的准确描述,即 \rho = \rho (T)。当然,在某些情况下,决定密度的因素也可以换成其他物理量,例如 Elder 问题中的盐浓度。
COMSOL Multiphysics 的单相流 接口中具有三种形式的动量和质量守恒方程:可压缩流动(Ma < 0.3)、弱可压缩流动 和不可压缩流动。如下图所示,您可以在层流 设置中方便地对可压缩性选项进行选择。
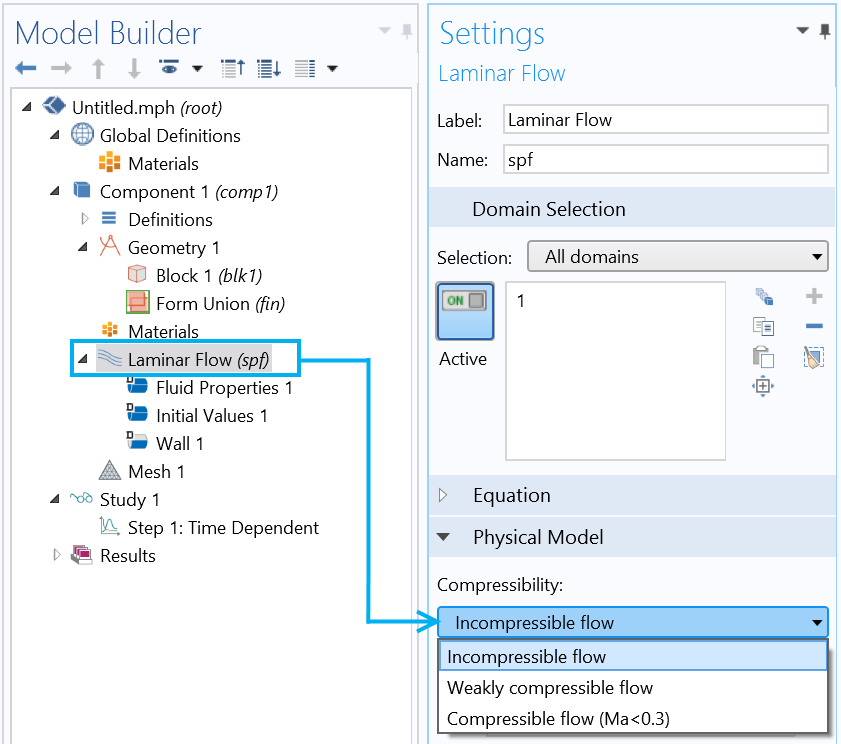
在 COMSOL Multiphysics 中选择可压缩性选项。
流体的各项物性通常并非恒定不变,它们取决于许多物理量。是否有必要在建模过程中加入这些物理关系由您自己决定。本文重点关注的是质量、动量和能量守恒方程,所以首先让我们回顾一下如何利用 COMSOL Multiphysics 处理不同可压缩性选项下的粘度 \mu、密度 \rho、导热系数 k 和热容量 C_p等物性参数。
我们将在下文中首先探讨等温流场仿真,然后再对非等温流场仿真展开讨论。
处理等温仿真问题
泵、搅拌器、机翼和多相系统……此类装置通常会被模拟为等温装置。等温流场仿真假设 \mu、\rho、k 和 C_p 均与温度无关。如果流体属性被定义为 T 的函数,则会使用参考值进行求解。这意味着能量方程会通过对流项与其他两个方程进行弱耦合,之后若有需要,再对此方程进行计算。然而,这样的近似处理方式并非总是可行的。
COMSOL Multiphysics 的用户界面(UI)赋予了我们相当高的自由度,我们可以先对单个物理问题进行研究和求解,然后再基于初始求解结果构建多物理场问题。请务必记住,能否忽略能量守恒方程与是否考虑温度场没有直接关系,低于特定的马赫数(Ma<0.3)才是忽略能量守恒方程的必要前提。
接下来,让我们看看如何针对自己的建模问题选择适合的可压缩性选项。
针对等温流动选择适合的可压缩性选项
可压缩流动(Ma < 0.3)
可压缩流动(Ma < 0.3)是最常用的选项,它并未对所求解的系统做出任何假设。COMSOL Multiphysics 将会对流体属性产生影响的所有因素均纳入了研究范畴。在等温流动中,温度通常是均匀的,流体属性(密度和粘度)保持不变,我们可以在参考值下分别对这些属性进行计算。即使如此,流体属性仍可能随着压力或其他物理量(例如浓度)的变化而变化。借助这一计算量最大的方程(NS方程),我们便可以模拟任意类型的流动,并能对不可压缩的情况进行描述。围绕一定攻角的 NACA 0012 机翼流场教学模型是一个使用了可压缩流动方程的案例。
弱可压缩流动
弱可压缩流动 是 COMSOL Multiphysics® 5.2a 版本中新添加的选项,其方程与可压缩流动(Ma < 0.3)选项基本相同。唯一的区别是,若密度会受到压力的影响,则需要在绝对参考压力下对密度进行计算。在这种情况下,与密度相关的所有因素(例如物质浓度)都会被考虑在内,所以我们仍可以通过此方程来计算由浓度梯度引起的体积力。
不可压缩流动
对于不可压缩流动 选项而言,只要可以将 \rho 作为常数(例如模拟低速流动的等温液体或气体时),该选项的方程便是有效的。这一选项也可应用于密度为常数的、互不相容的两相或三相流仿真中。当应用了不可压缩流动 方程后,COMSOL Multiphysics 会自动使用参考温度和压力对 \rho 进行求解。此外,它还会使用参考温度来计算 \mu。当然,在很多应用中,上述物理量往往依赖于另一个变量,例如物质浓度。对于此类情况,我们根据接口内多个变量的参考值对密度进行精确的计算。想了解更多信息,请下载净化水反应器的案例模型。
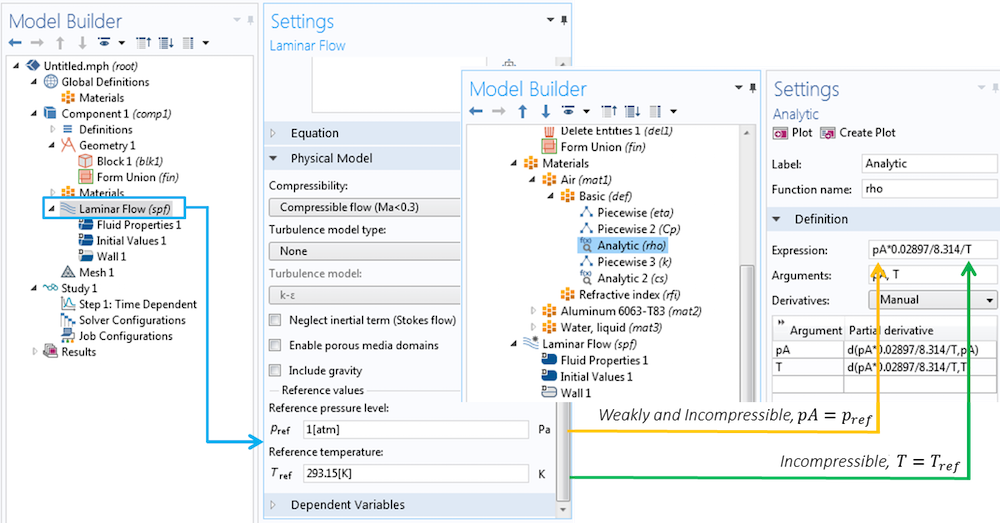
等温弱可压缩流动和等温不可压缩流动这两种情况下的密度设置细节。
此外请特别注意方程 栏中的方程形式,它会根据选定的选项而改变。
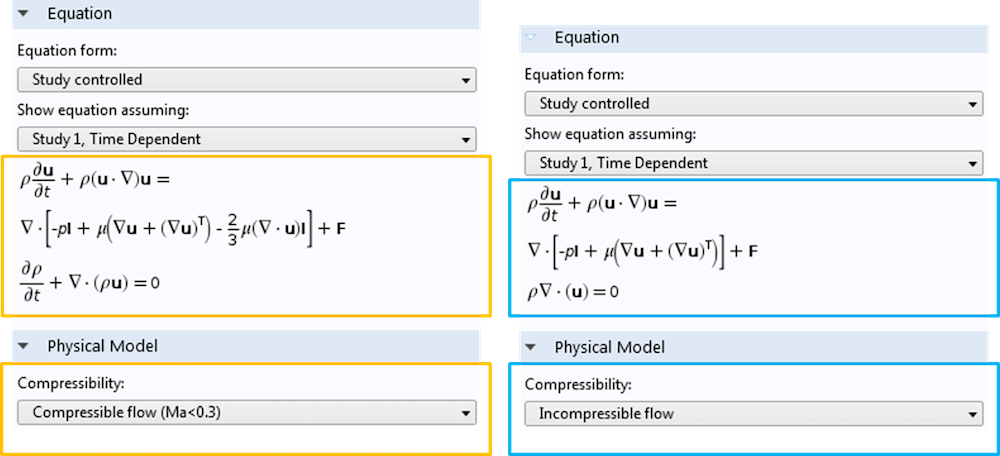
可压缩和不可压缩的 Navier-Stokes 方程各自具有不同的形式。
处理非等温仿真问题
非等温流场仿真通常涉及冷却和加热应用(即共轭传热)。运行此类仿真时可以参考由自然对流、强制对流或混合对流主导的系统。
根据所分析系统的类型和采用的假设,所有可压缩性选项均适用于非等温仿真。由于可压缩流动(Ma < 0.3)是处理高压力差作用下的气体的唯一有效的方程,所以我们在本文中只介绍低于马赫数极限的系统,以及那些自身的流体属性只取决于温度的系统。(提示:软件中有一个专门用于模拟高马赫数系统的接口,相关内容请参阅 Sajben 进气道教学模型)。由于能量方程中包含速度,所以方程系统中的质量、动量和能量守恒实现了完全耦合。与此同时,压力会明确地出现在动量方程中;温度会明确地出现在能量方程中;并且这两个方程中所涉及的流体属性可能同时包含了温度和压力的影响。
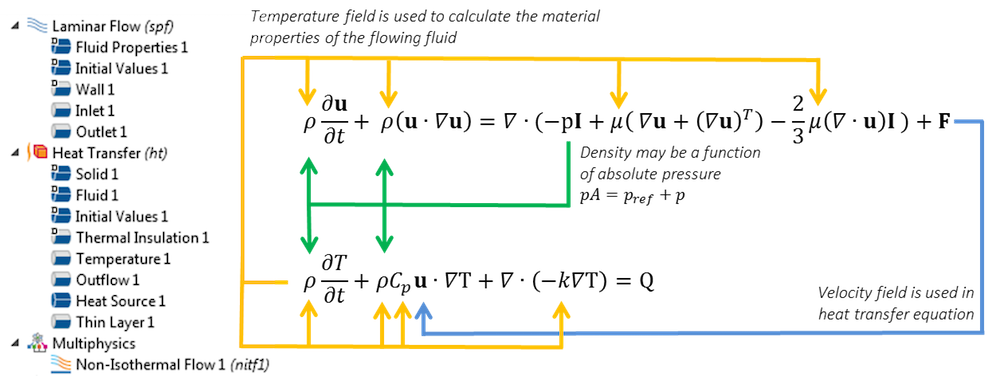
耦合了动量的能量方程。在自然对流的情况下,一部分体积力 F 取决于温度梯度。
针对非等温流场仿真选择适合的可压缩性选项
可压缩流动(Ma < 0.3)
在对流传热仿真中,可压缩流动(Ma < 0.3)选项可用来分析强制对流和自然对流。
强制对流指的是压力和温度会对流体属性产生不可忽略的影响。高速系统便符合这一情况,因为这类系统中的压力变化对密度的影响十分显著。如前文所述,液体的密度基本与压力无关,因此它的方程与弱可压缩流动 的方程完全相同。如希望了解更多信息,请参考我们的参数化管壳式换热器教学模型。
自然对流的驱动力来源于由温度梯度引起的浮力。对于封闭腔内的气体,我们必须使用可压缩流动(Ma < 0.3)选项,这样才能保证方程组的一致性。事实上,如果腔体体积和气体总质量为常数,那么平均密度也必须是常数。压力变化有助于抵消由温度变化引起的密度变化。您有兴趣模拟这样的系统吗?您可以参考灯泡内的自由对流教学模型,这一案例说明了如何利用辐射创建瞬态共轭传热模型。
弱可压缩流动
弱可压缩流动 选项的方程为简化形式,因此计算速度有所提升。在 COMSOL Multiphysics 中对预定义的非等温流 或共轭传热 进行耦合时,该选项为默认选项。此方程基本上忽略了上方图像中绿色箭头指示的方程耦合,可用于分析强制对流和自然对流。
对于强制对流的情况而言,弱可压缩流动 选项可应用于水或其他流体的仿真中,通常也可以模拟开放系统中的气体(参考散热器模型案例)。这些情况同样适用于自然对流体系,请参考保温瓶中的自然对流冷却案例。
不可压缩流动
不可压缩流动 选项同样能应用于强制对流和自然对流。在进行连续仿真时,初始情况下该选项仍然适用。比如说,有时先在参考温度下计算流场,然后在第二次仿真中计算温度场。当流体属性在模拟温度和压力范围内变化较小时,由此方式得到的估算值将十分精确。含液体的换热器案例便完美诠释了这一模拟方法。您还可以在处理高度非线性的静态问题时,应用此方法来获取更为一致的初始值。在使用“冻结速度”完成对流场和温度场的计算之后,将该结果作为全耦合仿真的初始值,可以大幅度提高全耦合问题的收敛性。
在上一种情况中,COMSOL Multiphysics 应用了 Boussinesq 近似。软件利用接口规定的参考温度和压力来计算密度、粘度、热容和导热系数。此外,它还会自动计算流体的热膨胀系数 \alpha_p,膨胀系数表示密度对温度(在参考温度T_{ref}附近变化)的导数,并通过它来施加浮力 F_b=-\rho_{ref}\alpha_p(T_{ref})(T-T_{ref})\textbf{g},其中 \textbf{g} 表示重力矢量。您也可以直接输入系数,如下所示。
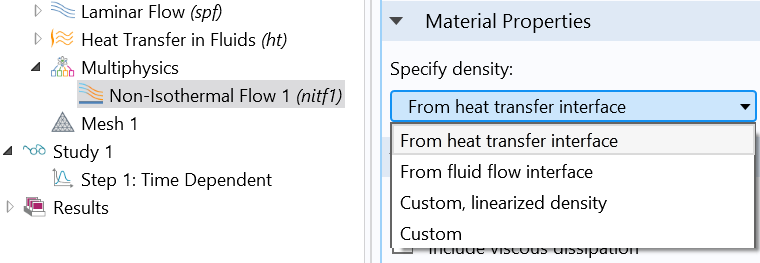
用于指定密度的选项。
边界条件的重要性
在使用重力选项时,请务必保持边界条件和初始值的一致性,这一点在模拟自然对流时尤为重要。这是因为体积力(即浮力)是作用在系统内部,所以我们不得不考虑到它的存在。含有静水压头的管道便是此类系统的一个示例。若边界本身与重力矢量不垂直,那么很明显我们不能简单地施加恒定的压力作为边界条件。
COMSOL Multiphysics 除了能模拟上述系统和情况之外,还能帮助您处理仿真中的初始值和边界条件。如希望了解更多信息,请参考重力和边界条件教学模型。
如何在COMSOL Multiphysics® 中模拟自然对流和强制对流
对于强制对流来说,流动和温度的耦合是在“多物理场”节点的层面上进行的。在非等温流 接口中,不仅对方程进行了耦合,流体流动和传热属性也实现了同步(参见下方截图)。根据选定的可压缩性选项,COMSOL Multiphysics 将在后台适当地更改流体属性,使之与选定的方程保持一致。此外,非等温流动 接口还负责执行温度壁函数和计算湍流的热传递属性。
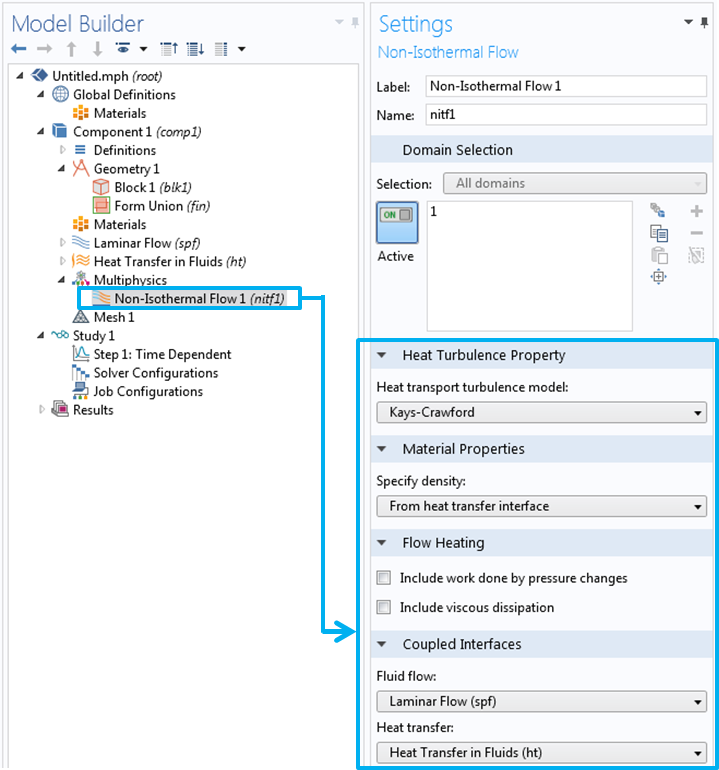
非等温流接口的设置窗口。
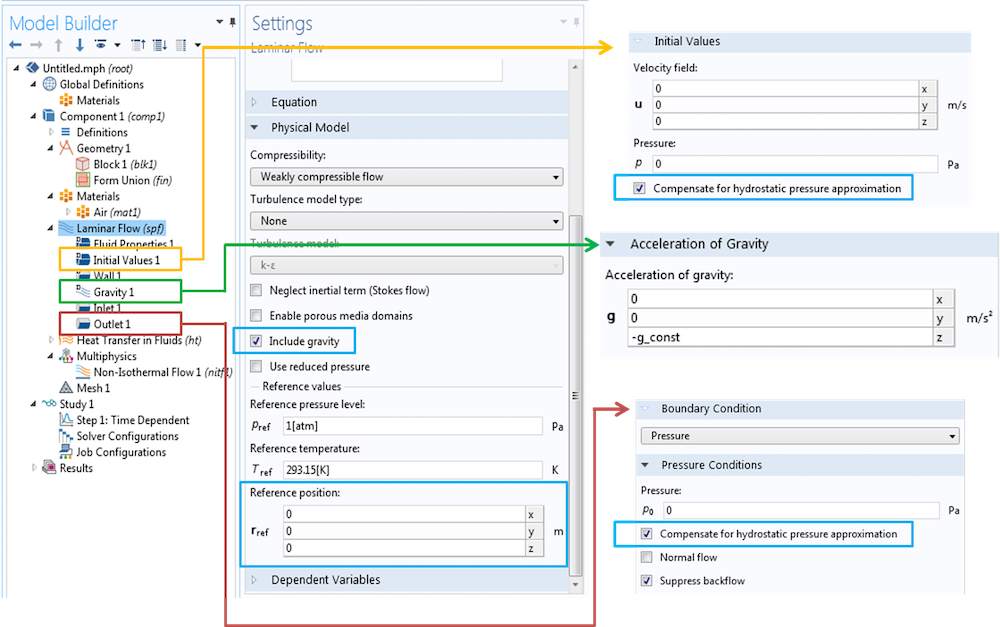
如果有必要在仿真中加入由温度或浓度梯度产生的浮力,则应当勾选包含重力 复选框。启用此特征后,参考值 栏中将会生成一些值,这些值可用于近似计算静压力,除此之外还会生成参考温度和参考压力。勾选包含重力 后,设置中还会出现一个新的子节点——重力。您可以在这个子节点中对作用于系统的加速度方向进行指定。添加了“重力”子节点后,在适当的情况下,在参考温度和参考压力下的流体静力学贡献会自动添加到边界条件中。
模拟自然对流时,您需要同时使用“重力”特征和非等温流 接口。二者结合使用,便能模拟在重力加速度作用下耦合的流场和温度场。
下方的仿真绘图取自保温瓶教学模型,此模型主要用于计算含热流体的保温瓶的热性能。保温瓶立在宽敞的房间的桌子上,瓶外开放空间中的空气便是此系统内的流动气体。针对上述案例的考虑方式让我们能更好地理解不同方程的用途、假设和结果。具体而言,可压缩流动(Ma < 0.3)选项对所有情况都是适用的。由于空气在开放的系统中流动,所以弱可压缩流动 选项同样是适用的。最后,由于密度变化很小,不可压缩流动 选项也非常适合用于对系统进行表征。
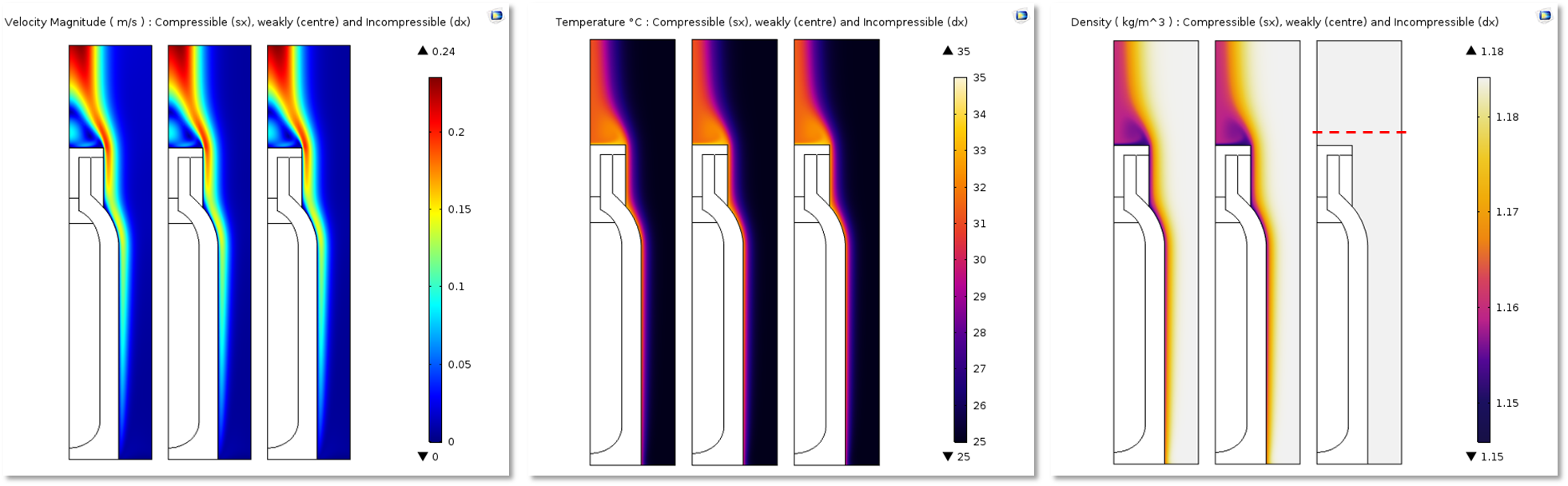
绘图对比了分别使用 可压缩流动(Ma < 0.3)、弱可压缩流动和 不可压缩流动方程计算出的速度场、温度场和密度场。我们只需切换这三个可压缩性选项,便可分别执行上述仿真分析。
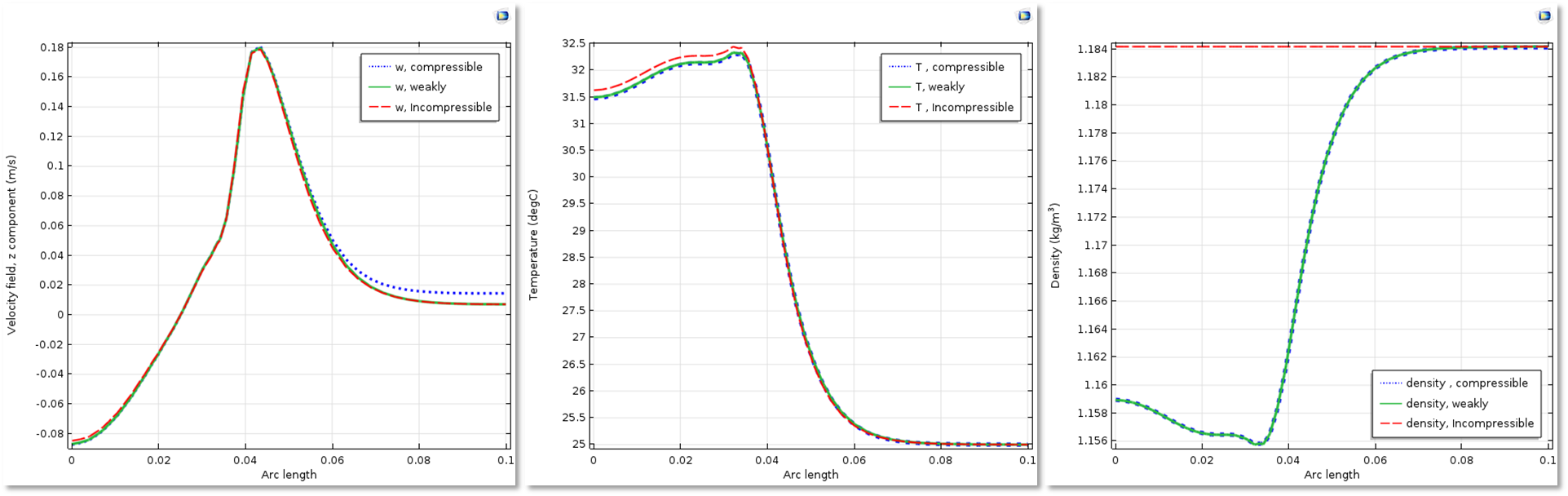
图像对比了分别使用 可压缩流动(Ma < 0.3)、弱可压缩流动和 不可压缩流动方程计算出的速度场、温度场和密度场。我们对上一组对比图进行了分析,并对右图红色虚线处 10 小时后的仿真结果进行了计算。
可压缩性选项的总结
选定合适的压缩性选项是准确、高效地求解流体系统的关键。借助 COMSOL Multiphysics 专业的流体仿真功能,您可以轻松地对自然对流和强制对流进行模拟,与此同时,软件还提供了多种模拟选择,让您全面掌控自己的仿真。软件强大的功能不仅优化了流体流动和温度场的数值分析方法,还帮助您进一步提升工程设计能力。
下方的表格可以帮助您针对自己仿真需求,选择最合适的可压缩性选项。
| 可压缩性选项 | 等温流 | 非等温流 |
|---|---|---|
| 可压缩流动(Ma < 0.3) |
|
|
| 弱可压缩流动 |
|
|
| 不可压缩流动 |
|
|
有关在 COMSOL Multiphysics® 中模拟流体流动和传热的更多资源
- 阅读相关博客,深入了解如何执行流场仿真并选择合适的接口
- 阅读相关博客,了解如何在共轭传热模拟中计算质量守恒和能量平衡
- 对本篇博客是否还有其他疑问? 请随时联系我们以获取帮助






评论 (2)
Xiaoxiao Wang
2019-04-30您好,流体的初始温度与位置坐标成e指数关系,但是修改之后会出现错误
兆宇 修
2025-02-19请问双相流,怎么分别设置一种可压缩,一种不可压缩呢