对于瞬态声学问题,有不同的声压级度量,一些文献和测量标准中对它们进行了定义。在将瞬态声学仿真的结果与声级计的测量结果进行比较时,或为了使瞬态仿真结果更容易在对数尺度上解释,了解这些指标非常重要。这篇博客,让我们来看看这些不同的指标是什么,何时以及如何计算它们。
定义声压级
对于稳态谐波噪声,声压级(\textrm{SPL})定义为:
式中,p_\textrm{rms} 是均方根(RMS)声压,p_\textrm{ref} 是参考声压(例如,空气的参考压力为 20 \mu \text{Pa},也是 RMS 值)。对于一个复振幅为 p 的谐波激励:
式中,{}^* 表示复共轭。因此,\textrm{SPL} 可以很好的定义稳态噪声,这里的表达式 \textrm{SPL} 可用于 COMSOL Multiphysics ® 软件中使用压力声学,频域 接口计算 \textrm{SPL}。接口中内置了几个变量,便于进行结果分析。
对于瞬态噪声,整个时间段(T) 内的 RMS 声压可以计算为:
由于此表达式在整个区间内取平均值,因此对于比较区间内随时间变化的水平没有用处。为此,我们可以分析其他指标。在这篇博文中,我们将重点关注:
- 使用频域到时域 FFT 研究中的使用窗函数 功能计算瞬态信号的频率权重 声压
- 使用时域的卷积计算时间计权声压级
- 使用参数扫描计算用户定义时间段内的时均声压级
频率权重
人耳不能平等地感知所有频率的声级。例如,耳朵对 1000 \text{Hz} 音调的感知比 100 \text{Hz} 音调的更敏感。为了在分析声音测量时从数学上考虑这种敏感性,引入了A 权重作为 IEC 61672-1:2013 标准的一部分。这一功能可以调整正在分析的噪声,用于补偿频率。
其他权重函数包括:
- C 权重:这是为了捕捉耳朵的非线性响应,例如高声压级的与频率相关的变化。
- Z 权重:这是一个平坦的响应,用于表示零权重。
正常频率范围内的这三个函数(A 权重、C 权重和 Z 权重)如下图所示:
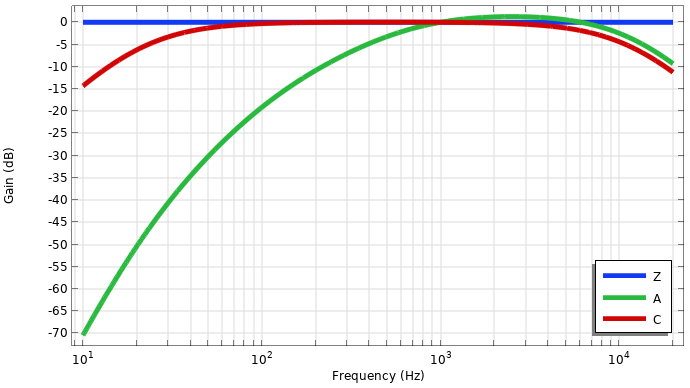
A-权重、C-权重和 Z-权重频率加权函数图。
权重函数的选择很大程度上取决于应用。例如,在美国,职业健康与安全管理局(OSHA)和环境保护署都使用 A 权重指标来衡量职业和环境噪声限值。
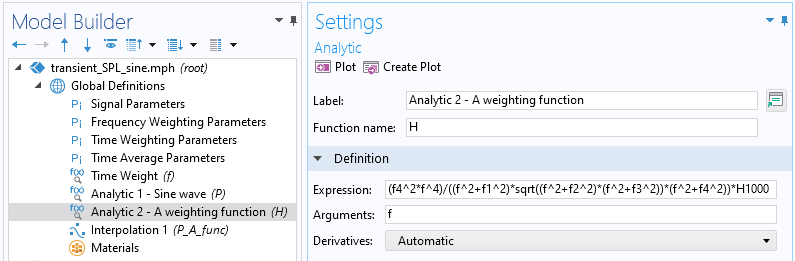
A 权重增益函数为:
{f_4^2f^4}
{(f^2+f_1^2)(f^2+f_2^2)^
{1/2} (f^2+f_3^2)^{1/2}
(f^2+f_4^2)}\frac{(1000^2+f_1^2)(1000^2+f_2^2)^
{1/2} (1000^2+f_3^2)^{1/2}
(1000^2+f_4^2)}
{f_4^21000^4}
式中,f 是频率,常数 f_1=20.6,f_2=107.7,f_3=737.9 和 f_4=12194。该函数被定义为在 1000 \text{Hz} 具有 0 \text{dB} 增益。稍后,我们将使用参数和解析函数来实现这个函数。
请注意,不同类型的权重内置在倍频带图中。该图可用于后处理所有频域数据。您可以在我们的博客文章“用于声学仿真的倍频带图”中详细了解该图。
时间计权声压级
考虑一个瞬态 A 权重声压 p_A(t)。可以通过以下方式定义瞬时声压级:
但是,这其中存在一些问题。首先,当 p_A(t) = 0 时,结果运算涉及取 0 的对数,所以 L_{p_A}(t) 未定义。第二个更实际的问题可以追溯到第一次使用声级计的时候。如下面的 3 个并排图像所示,针形指示器会上下移动以显示变化的信号。但是,如果我们根据瞬时声压级的定义来看待这一点,就会出现一个问题:指针来回移动的太快,以至于操作员很难在任何给定时刻看到读数。(参考文献 1)
声级计指针指示器。
为了克服这个问题,我们引入了时间计权声压级 的概念。其定义为:
在这个表达式中,\tau 是时间常数,\zeta 是用于积分的中间变量。参数 \tau 的定义是,慢速时间计权为 1s,快速时间计权为 0.125 s。按照这些规格制造的声级计有可供用户使用的慢速和快速时间权重选项。
时间计权声压为:
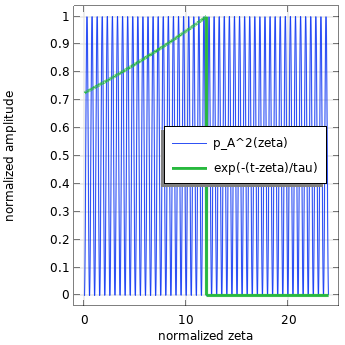
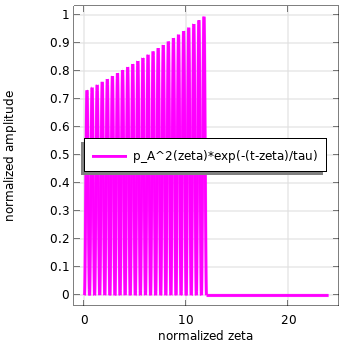
让我们来分解这个表达式。该函数是声压函数的平方和指数衰减函数的卷积。卷积将是两个函数相乘和积分的数学运算。在这个过程中,其中一个函数被翻转并沿中间轴移动,在这个例子中是 \zeta。假设使用 \tau = 0.125s 进行快速时间计权,用 p_A(t) = \sin{\omega t} 作为声压,当 t = \frac{6 \pi}{\omega} 的瞬间。 将 \zeta 通过在轴绘制这两个函数,以周期 T = \frac{2 \pi}{\omega} 归一化后进行可视化。
卷积积分中的各个函数(左)和卷积积分的被积函数,在离散时间将它们相乘的结果(右)。
当将两个函数相乘时,剩下用于积分是第三个函数,这个函数只有在由指数函数的当前时间戳计权的时间间隔上为非零。很明显,随着时间的增加,更多的指数函数与压力信号重叠,因此对于这种纯正弦曲线的情况,期望积分会增加到一个点。
回到实际示例中,时间常数有效地减慢了指针移动的速度,因此操作员可以在指针变化时实际读取它。尽管在数字技术之前它的用途是用于声级计,但时间计权声压级今天仍在用于现行标准和声级计。
等效连续噪声级
IEC 61672-1 中还定义了时间平均声压级,也称为等效连续噪声级。它的定义是:
平均周期 T 必须参考测量来指定,但可以代表任何时间。该标准建议声级计采用以下积分时间:T = 10 s、1 min、10 min、30 min、1 h、8 h 或 24 h。在这种情况下没有卷积。这只是一个定义的时间段内的 RMS。
时间平均压力为:
使用短平均周期(以秒或更短周期)被称为 短等效连续噪声级 或短 Leq。这对于减少数据存储和传输很有用,同时对于长时间记录的声音,仍然保持相当高的数据保真度。
示例 1:正弦压力信号
频率权重
在这里,我们展示了一个验证示例,该示例考虑了一个具有恒定振幅和恒定频率的简单正弦波形。这可以使用表达式为 P0*sin(2*pi*fdrive*t) 的解析 函数来实现。我们将使用参数来定义压力振幅 1\text{Pa} 和驱动频率 300\text{Hz}。第一步是计算 A 权重信号。我们将使用前面定义的参数为 A 权重添加第二个解析 函数。
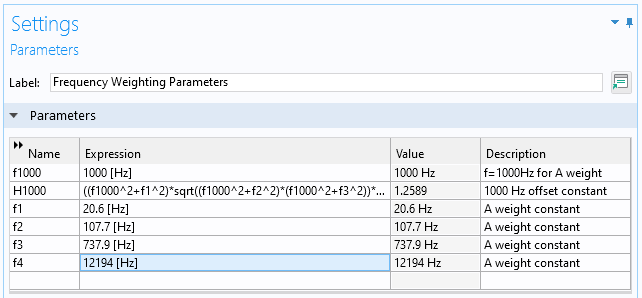
频率权重参数 的 设置窗口。
我们将在全局常微分 和微分代数方程 接口中添加一个 0 维组件并使用全局方程。
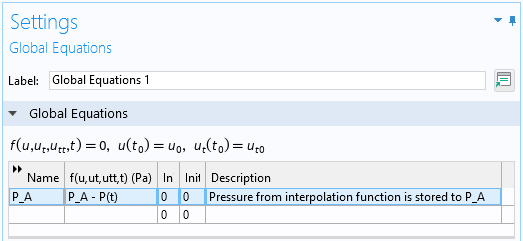
全局方程的设置窗口。
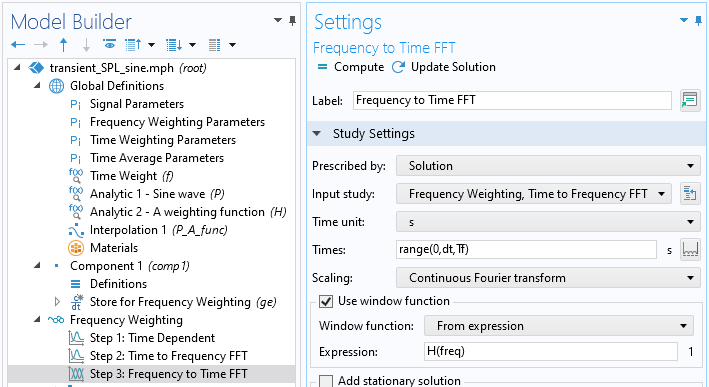
接下来,我们可以依次设置三个研究步骤。首先,瞬态 研究用于求解上图中定义的方程,它有效地将信号存储为一个因变量。接下来,时域到频域 FFT 研究将信号转换到频域。最后一步(也是涉及频率权重的步骤)是使用频域到时域 FFT 研究步骤。在这里,选择使用窗函数 复选框。对于窗函数,选择来自表达式 并插入我们之前定义的解析函数的表达式。
研究结果如下所示,放大到几个周期。A 权重压力与原始信号同相,但振幅减小。这种振幅的降低可以通过查看 A 权重频率增益函数曲线来验证,该曲线在 300 \text{Hz} 显示为 ~-7 \text{dB}。增益可以通过振幅的对数比来计算,即 20 \log_{10} \frac{0.445}{1} = -7.03,这与曲线一致。
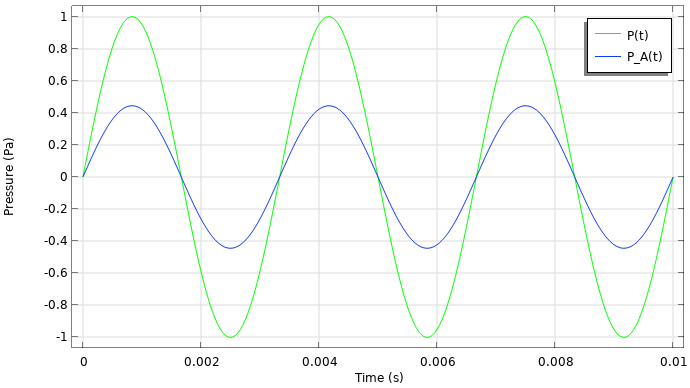
对正弦波形使用频率加重后的结果图。
时间权重
现在,已经对信号进行了频率权重,接下来我们将计算时间计权声压和时间计权声压级。首先,我们将新计算的值 P_A(t) 存储为插值函数,其数据源是一个派生值结果表。这样,我们就得到一个函数 P_A(t),用于计算卷积。
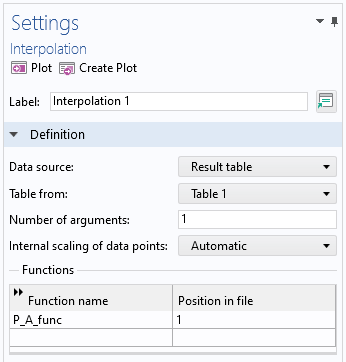
插值函数的设置窗口。
为了计算卷积,添加了一个 1 维网格 数据集。使用的表达式如下所示。在表达式中,\zeta 是网格定义的积分变量坐标。t 是为移动指数权重函数而引入的一个新变量。substval() 中的主要表达式是 integrate(P_A_func(zeta)^2*f(t-zeta),zeta,0,t,1e-8),它定义了 zeta 从 0 到某个变化量的积分 t,积分容差为 1e-8. substval()。用一个当前值 \zeta 替换 t,这使得卷积可以被计算出来。
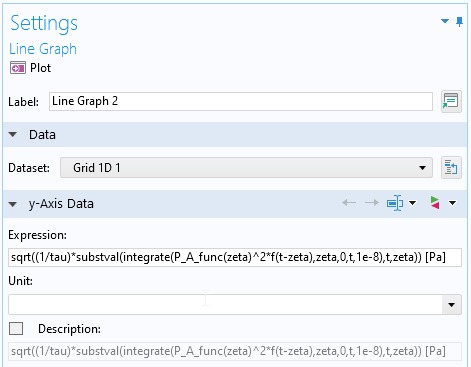
用于计算时间计权声压的设置窗口。
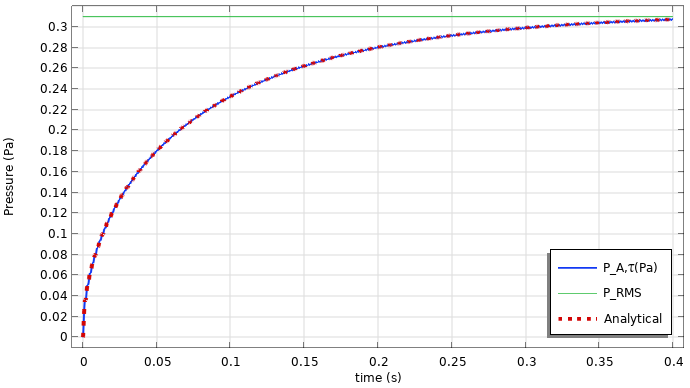
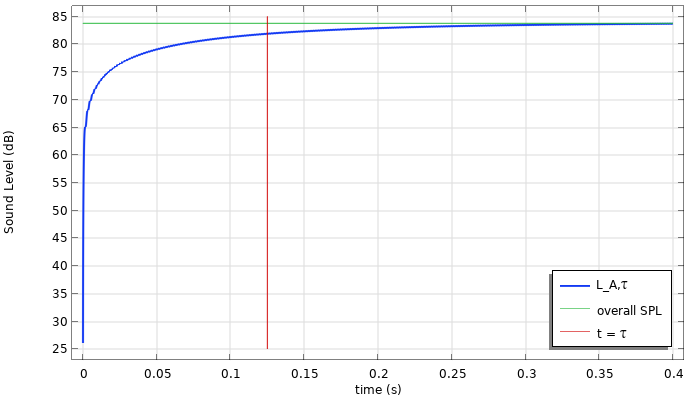
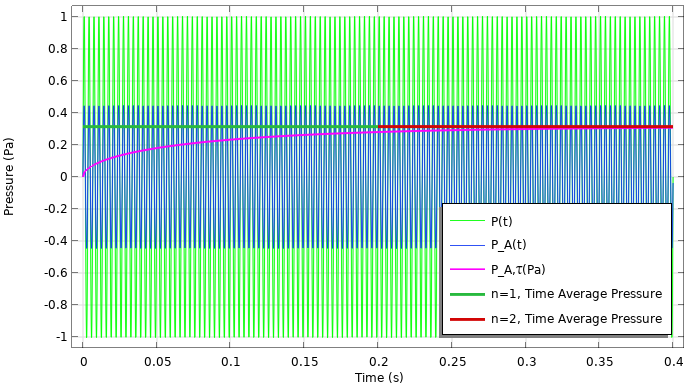
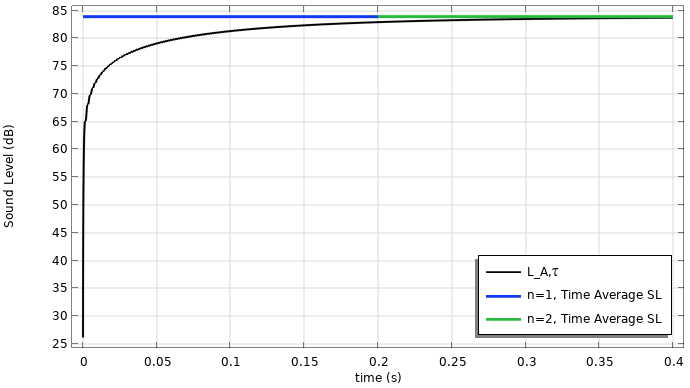
时间计权声压和声压级的结果如下所示。请注意,必须及时解析信号才能使积分准确。当波形是纯正弦波时,可能会发生一些有趣的事情。首先,随着时间的增加,快速计权声压和快速计权声压级分别接近 RMS 和总声压级。对于纯正弦曲线,可以根据卷积积分的解析解来检查结果,卷积积分可以按部分(多次)积分得出。如果 A 权重压力声压振幅为 P_{0A},则解析解为
此外,时间常数也可以解释为达到约 63% 等效水平的所需的时间。例如,以 dB 为单位的 63% 是 10 \log_{10}{63/100} = -2dB。所以,在 t=\tau,时间计权声压级应比等效声压级低约 2 dB(在这个示例中约为 84-82 dB)。
时间计权声压(左)和声压级(右)的结果图。
时间平均
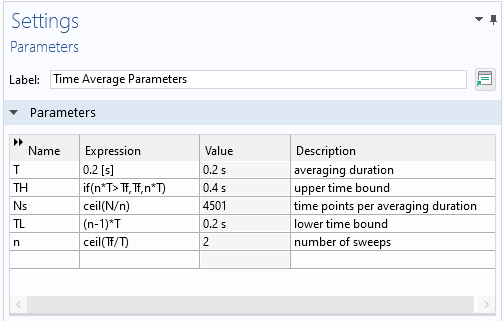
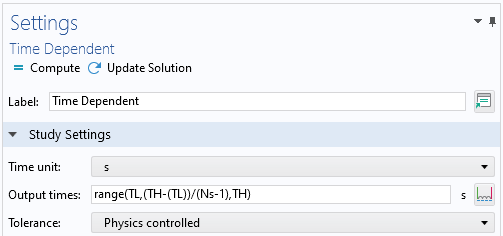
最后一步是计算时间平均声压级。我们将定义参数,包括平均持续时间、平均数以及积分的移动上限和下限。添加了一个新的瞬态研究,其中包含对平均值数量的参数化扫描。这个参数化研究的目标是创建可用于后处理的移动上限和下限。请注意,这里实际上没有解决任何物理场接口问题。
用于时间平均计算的 参数(左)和 研究(右)设置窗口。
线图可与参数解数据集一起使用,来绘制时间平均值。在这个图中,解参数 更改为手动,参数选择 更改为全部,时间选择 更改为最后。线段将从较低时间跨越到较高时间(x 坐标),表达式(y 坐标)是时间平均声压的计算值 P_{AT},并使用 timeint() 算子。
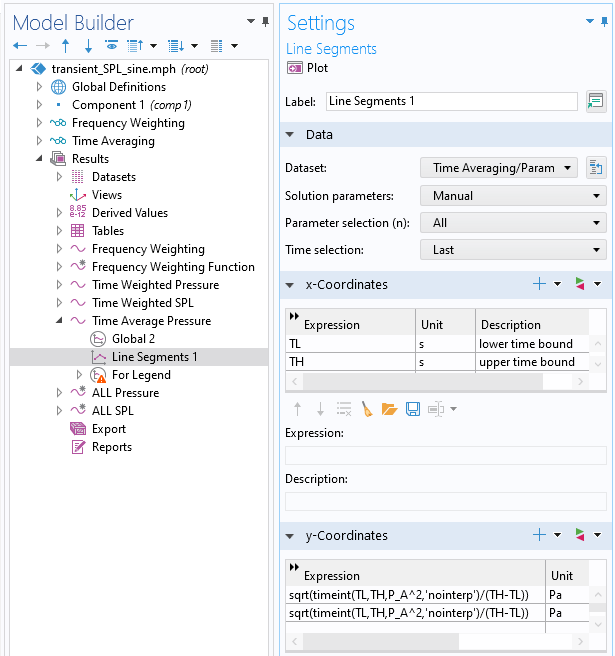
用于绘制时间平均声压的 线段设置窗口。
在这种情况下,平均时间远大于周期,因此时间平均声压是 RMS 声压。我们可以将所有结果绘制在一起进行比较。
正弦波的声压与时间(左)和声压级与时间(右)的结果。
示例 2:变速箱中的噪声
在之前的博客文章中,我们描述了如何对变速箱振动和噪声进行建模。使用这里描述的方法,我们可以对噪声进行后处理并绘制其他有用的指标。首先,我们将从位于坐标处的虚拟麦克风获取随时间变化的声压:
- x = 0.75 \text{m}
- y = 0 \text{m}
- z = 0 \text{m}
该数据被加载并存储在插值函数中。这些指标的计算方法与正弦验证的示例相同。
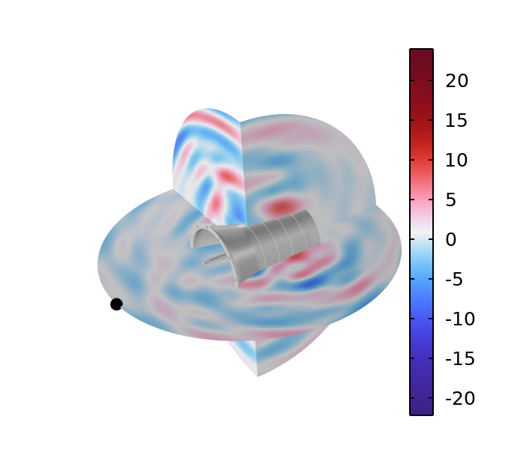
动态变速箱周围的声压场。时间 = 0.0020735 s。
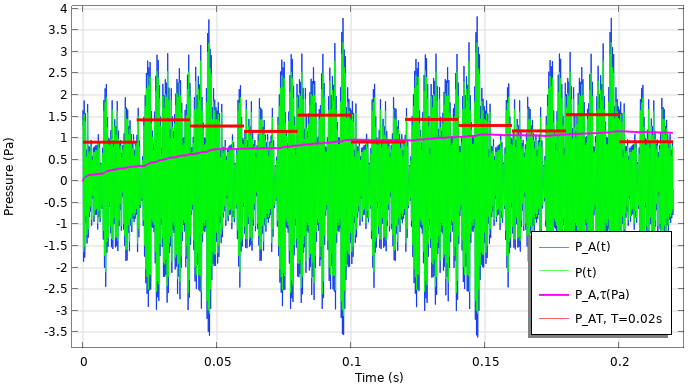
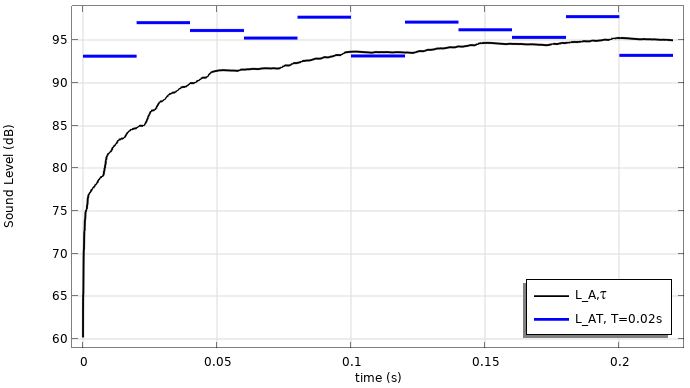
在这个例子中,我们将使用快速加权常数 \tau = 0.125s。平均周期为 T = 0.02s。结果表明,与原始信号相比,A 权重声压被放大。这是因为大部分声能在 1000-3000 \text{Hz} 频率范围。
变速箱噪声的声压与时间(左)和声压级与时间(右)的结果。
这里显示的结果是 A 权重、时间权重和时间平均声压和声压级。这些指标很有用,例如,如果你想使瞬态模拟的结果更容易在对数尺度上解释,将结果与声压级计的测量结果进行比较,或者对瞬态信号将如何被人耳感知感兴趣。
动手尝试
这篇博客,我们介绍了如何计算各种瞬态声学指标,包括频率权重、时间权重和时间平均。这里概述的定义和主要后处理步骤可用于任何瞬态声学仿真。单击下面的按钮,进入 COMSOL “案例库”。尝试自己动手建模:
参考文献
- E.H. Berger, The Noise Manual, AIHA, 2003.






评论 (2)
嘉豪 胡
2025-04-13Does COMSOL has the ability to compute the impedance of the local reacting liner by a 3D-model without any simplification?
Hao Li
2025-04-16 COMSOL 员工您好!
感谢您的评论。
可以直接仿真三维的声阻抗,可参考案例:
https://cn.comsol.com/model/input-impedance-of-a-tube-and-coupler-measurement-setup-time-domain-mor-using-partial-fraction-fit-129911
如果有进一步问题,建议您联系COMSOL的技术支持团队:
在线支持中心:cn.comsol.com/support
Email: support@comsol.com
谢谢!