我们总是希望能通过有限元方法来模拟会在其他域内旋转或平移的固体对象；此时，就可以使用 COMSOL Multiphysics 中的变形网格接口。本篇博客将分析一些会在其他域内发生大型直线平移或旋转的域，并将介绍各种可用于分析此类问题的有效建模技巧。
直线平移通过域的对象
在 “借助变形网格接口模拟平移运动” 博客中，我们曾讨论过如何模拟在流体或真空域内平移的对象。我们在该初始方法中用到了变形网格接口，还引入了四边形（或三角形）变形域的概念，其中的变形由双线性内插定义。如果能对移动对象周围的区域进行合理网格划分，那就能通过该技巧来分析大变形，但这并不总是可行。
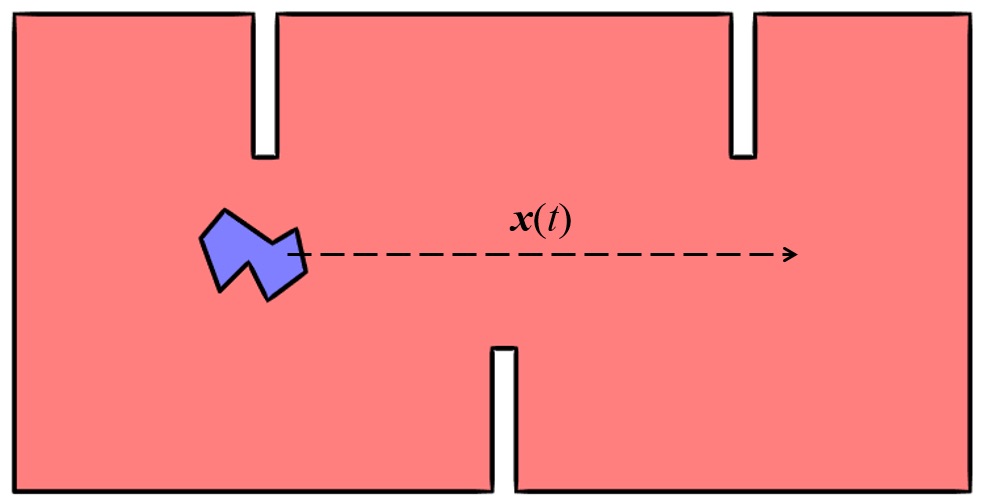
在复杂域内沿直线路径移动的固体对象。
在上例中，一个对象沿一条由 \mathbf x(t) 定义的直线路径通过一个侧边有突起的域。就很难应用原来的方法，那该如何处理呢？
使用滑动网格处理大型直线平移
求解分为四步，分别是：
- 在这两个域中创建几个不同的几何对象
- 通过形成装配体 功能设定一致对
- 通过之前设定的网格变形技巧定义直线运动
- 使用一致对保证求解物理场的连续性
我们首先应将原始模型空间分为两个不同的几何对象，如下图所示。其中，红色域表示稳态域，蓝色域是对象正进行直线平移的区域。分割过程将在几何序列内实现，最终通过形成装配体操作完成。
有关此功能的介绍及操作步骤，请观看相关视频。
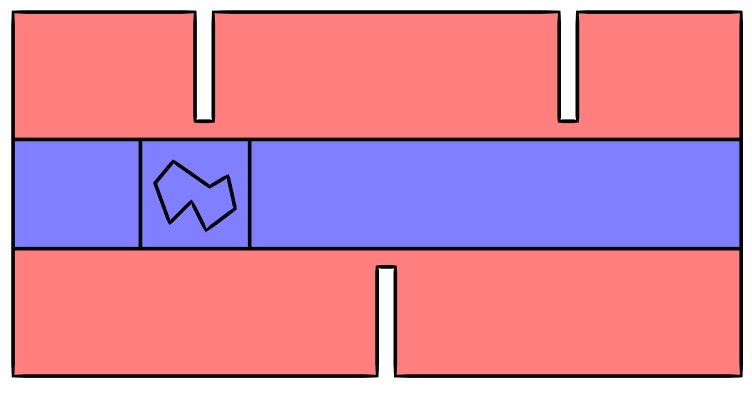
将模拟空间分割为几个不同的几何对象。
形成装配体步骤支持蓝色域内的有限元网格相对红色域内的网格滑动。该步骤将自动引入一致对，可用于维持场在求解域内的连续性。我们将分析适用于该情况的一类代表网格。
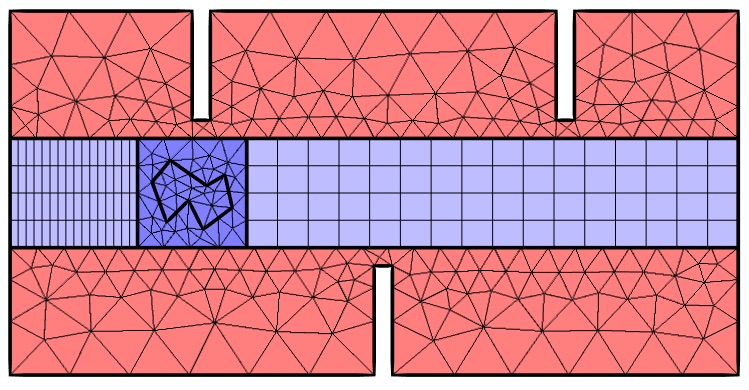
包含代表网格的分割域。
请注意，上图中暗红色域内的网格不会移动。同时，深蓝色域中的平移已通过已知函数 \mathbf x(t) 完整定义。淡蓝色域为网格将变形的区域。我们只需在这些域中使用之前介绍的双线性内插。您还可能注意到，这两个矩形区域中使用了映射网格，并调整了单元的分布，使它们的尺寸尽量接近或小于相邻的不变形单元。
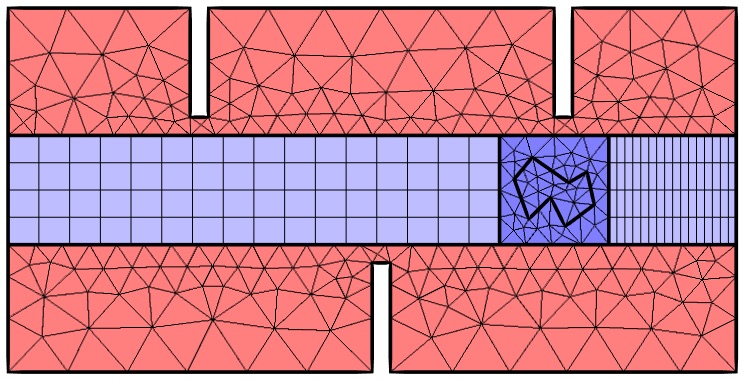
当对象沿直线平移后，淡蓝色域中的网格将变形。
保持解的连续性
从上图中可以清楚看到，移动与稳态域之间的网格并未对齐。虽然 COMSOL Multiphysics 5.0 版本极大提升了对域间网格未对齐情况的处理精度，但使用此功能时还应注意其他几点。
执行形成装配体完成几何步骤，COMSOL Multiphysics 会自动生成一致对，即网格未对齐的接触面。我们只需指示模型内所有的物理场接口应维持这些边界处的连续性。这可以通过对 > 连续性 边界条件实现，该边界条件在所有物理场接口可用。
增加此特征并应用于所有一致对后，软件会在边界处增加其他条件，以保证解在网格不连续处尽量平滑。每个一致对都包含源侧 与目标侧。在所有网格设置中，目标侧的网格都应更细。
具有非连续性网格的装配体网格适用于大部分物理场接口。不过，还是存在一些重要例外。该方法不能用于求解矢量场中涉及旋度算子的电磁问题，包括三维电磁波 接口、三维磁场 接口、三维磁场和电场 接口等。即便如此，我们还是可以将它用于许多物理场。
我们将查看需要计算对象周围温度场的情况，对象及周围域外壁的温度不同。下图为温度场的等值线图，验证了解在网格不连续的边界处仍相当平滑。
一致对中所用连续性边界条件处，温度场随时间的变化很平滑。
旋转对象
现在，您可能已经知道如何将该技巧用于旋转对象。我们只需在旋转对象的周围创建一个圆形域，并使用上文讨论的技巧即可。当然，如果对象只是在旋转，我们将不再需要变形网格，所以更容易实现。
下图中的对象与上文相同，但正在旋转。
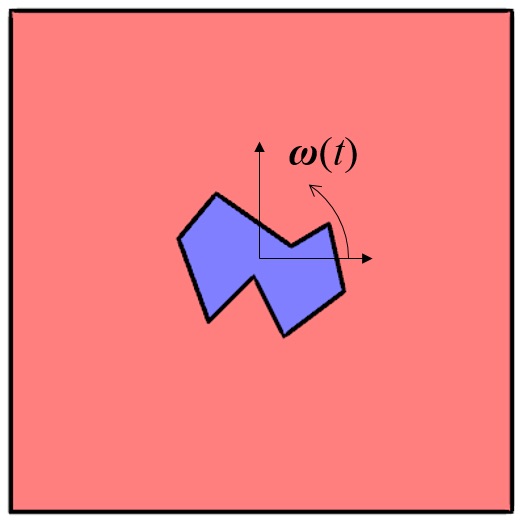
绕一个点选择的对象。
包含固定及旋转对象的装配体以及网格。
通过表达式指定旋转域 (X_{r}, Y_{r}) 中的变形，表达式可以包含以下项：角频率 \omega、未变形几何的坐标 (X_{g}, Y_{g})、对象的旋转点 (X_{0}, Y_{0})、时间 t。得到以下表达式组：
在变形几何接口中的指定变形非常简单：
看上去容易，对吗？事实上，当使用 COMSOL Multiphysics 中旋转机械、流体流动 和旋转机械，磁 物理场接口时，软件会自动应用本节介绍的技巧。博客向您揭示了这些接口背后的实际工作原理。
结束语
我们向您介绍了如何模拟流体或真空域中固体对象的移动。虽然我们在所有案例中都只是简单指定了位移，但其实也可以计算固体对象的位移，并耦合到周围区域的场解中。我们将在后续博客中对此进行介绍。
希望了解有关如何在建模中使用变形网格借口的更多信息吗？欢迎下载我们 App 库中的相关模型。
评论 (31)
笑阳 雒
2019-04-02您好 请三维模型中用什么物理场啊
Haili Wang
2019-04-15 COMSOL 员工三维和二维模型都是使用移动网格物理场，不过最新版本的COMSOL中不需要接口，直接在组件下定义即可，具体可以参考下述链接中的案例：http://cn.comsol.com/model/fluid-structure-interaction-361
凯鹏 刘
2020-06-07你好，请问如何实现物体沿直线运动的同时还能旋转呢
凯鹏 刘
2020-06-07已经通过修改指定变形的公式搞定了
某人 王
2020-07-03兄弟你做的是二维旋转移动还是三维的？
澍海 张
2021-04-14您好 您是怎么实现的 可以分享吗？
金辉 俞
2021-10-10您好，我正在做这方面的仿真，可以请教一下同时平移和旋转是怎么实现的吗？
孟雄 付
2021-11-03请问您解决了吗？想请教一下，我最近也在做旋转加直线运动的模拟，头都大了，可否用邮箱沟通756019387@qq.com
儒合 李
2022-03-17你好，请问您解决了吗？想请教一下，我最近也在做旋转加直线运动的仿真，可否用邮箱沟通109763640@qq.com
颖 刘
2021-11-29请问同时平移和旋转是如何实现的？
颖 刘
2021-11-29您好，我正在做这方面的仿真，可以请教一下同时平移和旋转是怎么实现的吗？
Qihang Lin
2021-11-30 COMSOL 员工您好，平移还可以参考这篇博客：http://cn.comsol.com/blogs/model-translational-motion-with-the-deformed-mesh-interfaces
平移和旋转都可以参考本博客中使用的案例：http://cn.comsol.com/model/modeling-deforming-meshes-30561
儒合 李
2022-03-17你好，可以请教一下吗？做了好久没做出来
可鑫 张
2022-04-27您好，您做出来了吗？可以请教一下这怎么既平移又旋转吗？谢谢
张某
2023-05-02您好，请问如何设置指定变形的公式来实现物体的平移与旋转呢，是否可以通过邮箱745435834@qq.com，来向您请教呢
冰 李
2023-05-16可以请教下您 怎么做吗 lllbin.314159@gmail.com
捷 周
2020-07-29您好，请问如何定义位置环境力作用下的网格移动？
洋洋 张
2020-07-29 COMSOL 员工问题有些模糊，无法为您详细解答，请将问题细化发送support@comsol.com，我们会有专业工程师为您解答！
可鑫 张
2022-04-27怎么样才能沿着一条直线既平移又旋转呀？
Qihang Lin
2022-04-29 COMSOL 员工可以尝试利用动网格物理场接口来进行定义，把旋转和平移写一个条件中进行模拟。
毅翔 冯
2022-10-11您好 请问可以在旋转的同时加入流场、电化学的阴极保护等多个场耦合模拟吗
Qihang Lin
2022-10-21 COMSOL 员工变形网格接口为通用接口，可以与任意物理场耦合，理论上可以实现您提到的这些场的耦合模拟，但现在没有现成案例需要您自己尝试。
朴真 郑
2024-03-27您好，我对于您的想法很感兴趣，请问现在有上述成功的案例可以交流一下吗？我的邮箱2498143280@qq.com，希望能请教一下。
冰 李
2023-05-16三维旋转怎么实现
Qihang Lin
2023-06-01 COMSOL 员工与二维旋转原理类似，三维中也可定义旋转域进行旋转
RICHARD 刘
2023-09-06旋转磁场需要画动网格吗
Qihang Lin
2023-09-07 COMSOL 员工用背景场的话可以直接定义为随时间旋转的函数，则不需要。如果是由磁体、线圈产生的磁场在旋转，则可能需要用动网格功能。
韬 杨
2024-03-10你好，示例中划定出的动网格区域不仅包含了固体区域还包含了一部分流体区域，这部分流体也会随着动网格平移或旋转吗？这怎么理解？
Hao Li
2024-03-11 COMSOL 员工您好！
感谢您的评论。
示例中变形的区域是块体及周围区域以外的区域，从上图可以看到块体及周围区域是不发生变形的区域，其以外区域被压缩和拉伸了。
如果有进一步问题，建议您联系COMSOL的技术支持团队：
在线支持中心：cn.comsol.com/support
Email: support@comsol.com
谢谢！
Kun Wang
2024-04-24你好，请问comsol可以模拟磁针在磁场中的旋转吗，如果可以，我该怎么弄呢
没延 韩
2024-04-26 COMSOL 员工可以。使用“磁场，无电流”和“固体力学”接口，并添加“磁力学”耦合节点。磁场无电流接口可以添加背景磁场也可以通过场源加磁场，磁针旋转会带来空间磁场变化，所以外部空气域可以使用动网格中的变形域进行描述。参考案例“带屏蔽线圈的交流接触器”：http://cn.comsol.com/model/ac-contactor-with-shading-coil-102771